基于声速梯度的声纳浮标工作深度选择∗

章尧卿 胡柱喜 刘 克

（1.海军航空大学 烟台 264001）（2.91049部队 青岛 266000）

1 引言

海洋环境对声纳作用距离的影响主要表现在声速梯度、海区深度、海底底质和海况等方面。在等温层或弱负梯度层环境下，声波基本为直线传播，声波能量在空间分布比较均匀，此时声纳作用距离只取决于声纳系统本身和目标声学特性［1］。但在非良好水文条件下的声波不是直线传播，声波能量在空间也不是均匀分布的，这时声纳系统作用距离还与声速梯度、声纳深度和目标深度有必然关系，其中，声速梯度对作用距离影响最大［2］。下面主要针对不同的声速梯度来分析声纳浮标的工作深度问题。

2 声速梯度的影响因素

对于大多数海洋区域而言，声速的垂直梯度约为水平梯度的1000倍。仅暖流和寒流交汇区域，水平梯度有时与垂直梯度相比拟。因此，在一级近似下，可以把海洋看作是一种平面分层介质，其声速特性仅随深度变化而变化，而在水平面内保持不变［3］。

声纳浮标搜潜系统包含温度深度测量浮标，用来测量海区的温度-深度剖面。温深浮标的测温探头在入水后以一定速度下沉（约为1.5m∕s），下沉过程中实时将海水温度发回监听飞机［4］。温深浮标并不是直接测量海水声速，而是测量不同深度处海水介质的温度，再通过相应的换算公式将温度连同其它因素转换为声速。

声波在海水中传播的速度与海水温度、盐度及静压力有关。海水的温度越高，盐度和深度越大，声速越高。鉴于影响声速的因素复杂，难以由理论计算求得，为此经大量实测，建立了如下的经验公式［5］：

c=1450+4.21T-0.037T2+1.14(S-35)+0.0175H

（1）式中：c为声波传播速度，单位m∕s；T为海水温度，单位℃；S为海水盐度，单位‰；H为水层深度，单位m。

通过分析上式可以看出，温度增加1℃，声速变化近似4m∕s；盐度每增加1‰，声速增加1.14m∕s；压力增加1个大气压，声速增加0.175m∕s。在影响声速大小的温度、盐度和静压力（或深度）几个因素中，以温度影响最为显著。在使用声纳浮标的有限范围的海区内，其盐度和压力的影响通常是较小的，相对于温度对声速的影响可以忽略不计，通常在计算时将其设为常数［6］。

3 海洋声速垂直剖面的类型

在海洋表面，由于受到海面的冷热交换和风浪的搅拌作用，在海表以下一定深度内海水温度基本不变，形成混合层；混合层的深度在不同的海域各不相同，对应到声线剖面上，由于温度不变，海水的声速主要受压力的影响，随深度增大缓慢增大，形成一个声速梯度为正梯度的声学层，该层的最大深度称为声学层深度［7］。在混合层下，随着深度的增加，海水温度急剧降低，形成温跃层，对应的声线剖面上出现一个负梯度的声速层。随着海深的继续增大，到一定深度，海水上下层的热量交换基本达到平衡，温度基本不变直至海底，形成深海等温层。反映在声线剖面上，受海水的静压力影响，声速随深度增大［8］。

在典型沿岸浅海及大陆架上，声线剖面受到较多因素的影响，比深海有更大的变动性，但平均而言，仍然有比较明显的季节特征，在冬季的典型声线剖面是等温层，而在夏季则为负跃层［9］。

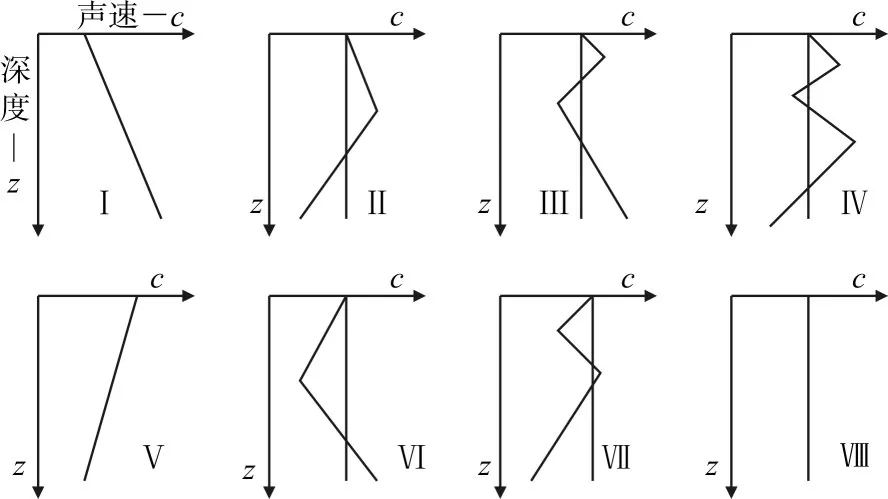
图1 垂直声线剖面类型

根据理论分析，海洋中声线剖面垂直分布类型共有如图1所示的八种类型。但这八种类型只是理论上的抽象分类，从理论原则上进行分类指导，具有理论指导意义。实际的海洋环境中，声线剖面可能更为复杂，所以在实际使用中要结合具体的海域水声环境特点来确定具体的声速类型。

图中在中纬度的深海环境中可能出现的声速垂直剖面类型为第III种、第VI种类型，在两极海域会出现第I种类型的声速垂直剖面，其它的类型基本不可能出现在深海环境中［10］。由于浅海环境的复杂多变，这八种声速类型都有可能出现，只是声速梯度与深海环境相比要小很多。判断所处海域声线剖面类型更为准确的方法是根据海区的声线剖面历史数据进行分析。

4 分层介质中的声线轨迹

海洋中声波的传播在数学上可以用波动方程的解来描述，这个解是在特定问题的相应边界条件和介质条件下得到的。波动方程是声压p对坐标x、y、z和时间t的偏微分方程，可以写为

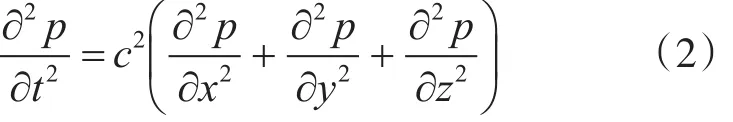
式中，c是具有声速量纲的量，并可随坐标变化。

有两种理论方法解波动方程。一种是简正波理论，另外一种解法是射线理论。射线声学具有形象直观的优点，它用声线图给出传播的图像。但是，在一个波长的距离内，射线的曲率半径或声压振幅有较大的变化时不能给出完美的解［11］。但是，射线声学本身有其明显的优点，就是简单、明了、物理意义清楚，因而在解决某些问题和分析某些现象时是必不可少的。对于高频情况，射线理论有足够的准确性［12］。

在确定海水中声线轨迹的时候，我们最关心的是分层介质中的声线轨迹。由于分层介质的声线剖面，可以看作是很多层线性的声速断面的合成，所以我们首先来说明具有线性声线剖面的情况。在这种情况下，声速c与深度z的关系为

其中g为声速梯度，A是一个常数，z代表深度。

声线轨迹上两个点的深度差Δz=z2-z1可以由式（3）求出：

应用斯涅尔（Snell）定律（见图2）：

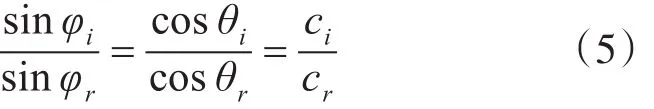
式中φi和φr分别表示声线入射路径和折射路径与分界面的法线之间的夹角；θi和θr分别为入射声线与折射声线与分界面之间的夹角。ci和cr分别为入射声线与折射声线所在介质中的声速。由式（4）可知，如果用c0表示声线在水平时的声速，那么任何深度上的声速可以表示为

将式（4）和式（6）合并得到：

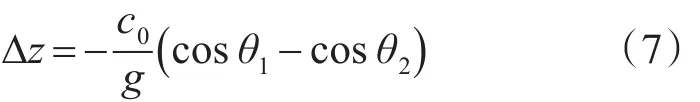
将上式积分，便得到：

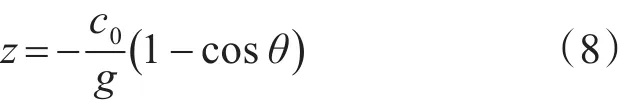
这是一个曲率半径为-c0g的圆弧方程。

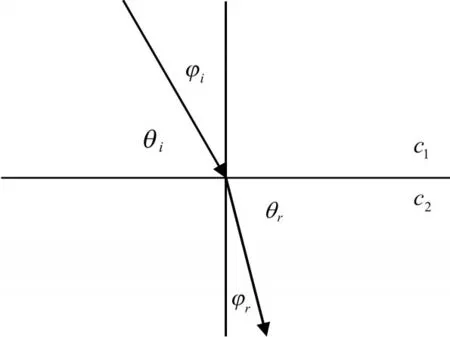
图2 斯涅尔定律示意图

如果声线剖面不是线性的，那么我们可以用分层的方法进行处理，用折线去逼近任意形状的剖面。在每一段折线所对应的那一层海水中，声线轨迹都是圆弧，区别是圆弧的曲率不同，整条声线就是由一段段具有不同曲率半径的圆弧连结起来的。

当g＞0时，称为正梯度，这时曲率半径为负，声线朝上弯曲；当g＜0时，称为负梯度，这时曲率半径为正，声线朝下弯曲；当g=0时，曲率半径为无穷，声线轨迹为直线。

5 深度设定实例

根据射线声学理论，由于声速梯度的分布和声纳所处的深度不同，造成从声纳发出的所有声线中只有一部分声线将通过海水中的某一个局域范围。当声线足够密时，把各声线的声强相加求平均，可作为这一局域范围中心声强的近似值。从直观上来讲，在声线轨迹图上声线密度较大的地方，传播到的声能量较大，传播损失较小，反之，声线密度较小的地方，传播到的声能量较小，传播损失较大［13］。通过声纳方程的分析可以知道，在其它条件不变的情况下，某一点的传播损失越小，那么声纳就越容易发现该处的目标。所以通过声线轨迹图可以指导给出声纳浮标的最佳工作深度，下面就给出几个实例。

图3给出的是黄海某处2、4、11三个月份声速的垂直分布图，海深为70m。其中2月份的声速呈现轻微的正梯度；4月份的声线剖面属于声道型，但是由于声速随深度的变化并不明显，基本上可以将其视为声速均匀分布；11月份的声线剖面为典型的负跃层情形。

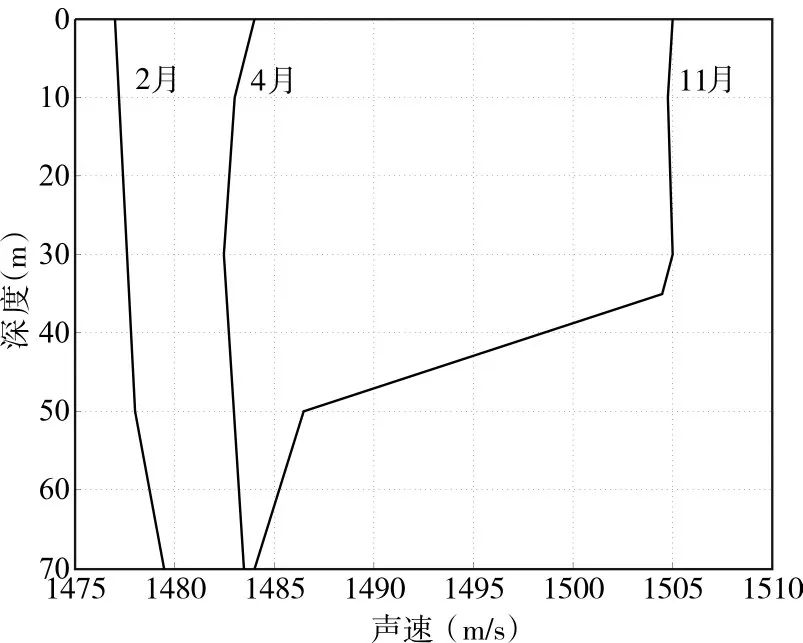
图3 黄海某处不同月份声速垂直分布

下面就采用射线理论，通过仿真计算绘制出这三个月份的声线图，分别如图4、5、6所示。三幅图中（a）图都是假设声纳浮标工作深度设定为15m，（b）图都是假设声纳浮标工作深度设定为40m（由于海深只有70m，故没有考察声纳浮标的另外一个工作深度150m）。

6 结语

通过实例仿真计算，分析可得出如下结论：

1）图4的声线剖面呈现轻微的正梯度，从声线图上可以看出，不论浮标位于15m还是40m，声线都轻微的向海面弯曲，海面附近传播损失较小，也就是说这两个深度均比较适合于探测靠近海面的潜艇目标。再进一步比较两个不同深度声线轨迹的细微差别可以看出，如果潜艇目标位于30m以下的区域，浮标工作于40m的深度可以具有更大的探测距离。所以综合起来就是，在轻微负梯度的情况下，应当将声纳浮标置于靠近潜艇目标可能深度的附近。

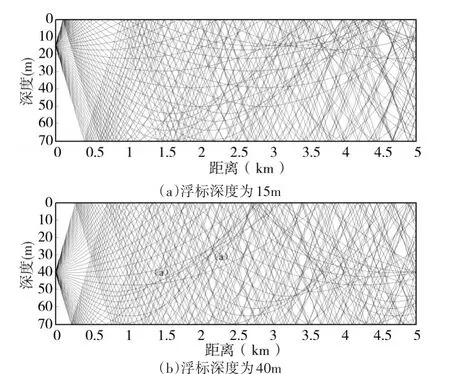
图4 黄海某处2月份声线剖面图

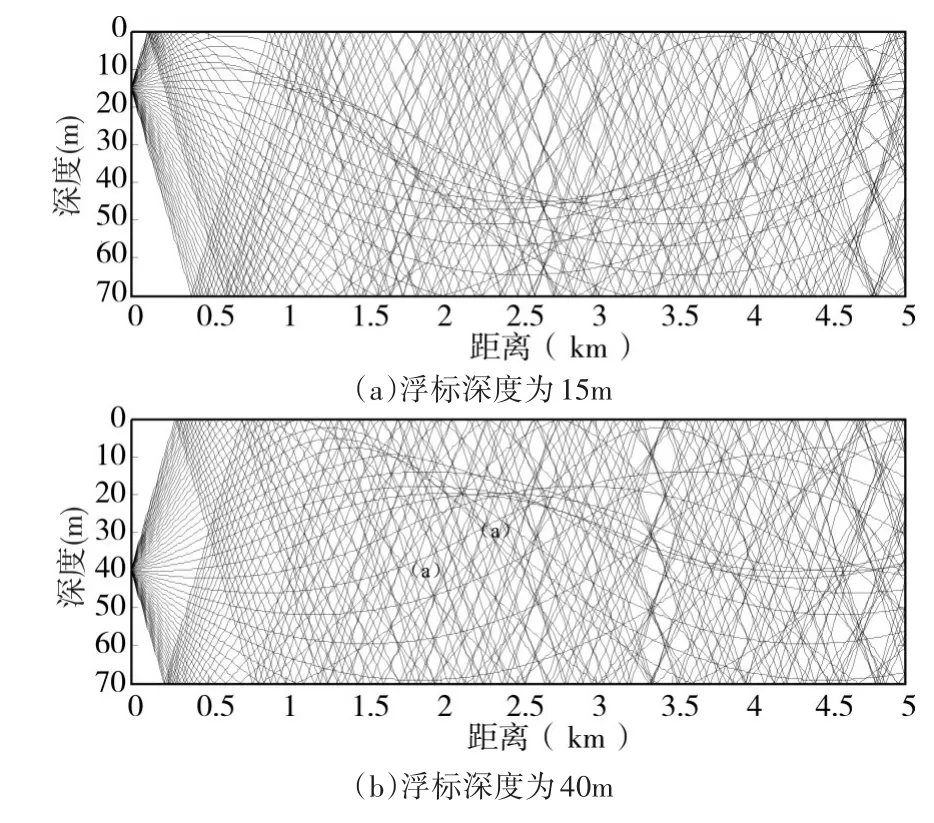
图5 黄海某处4月份声线剖面图

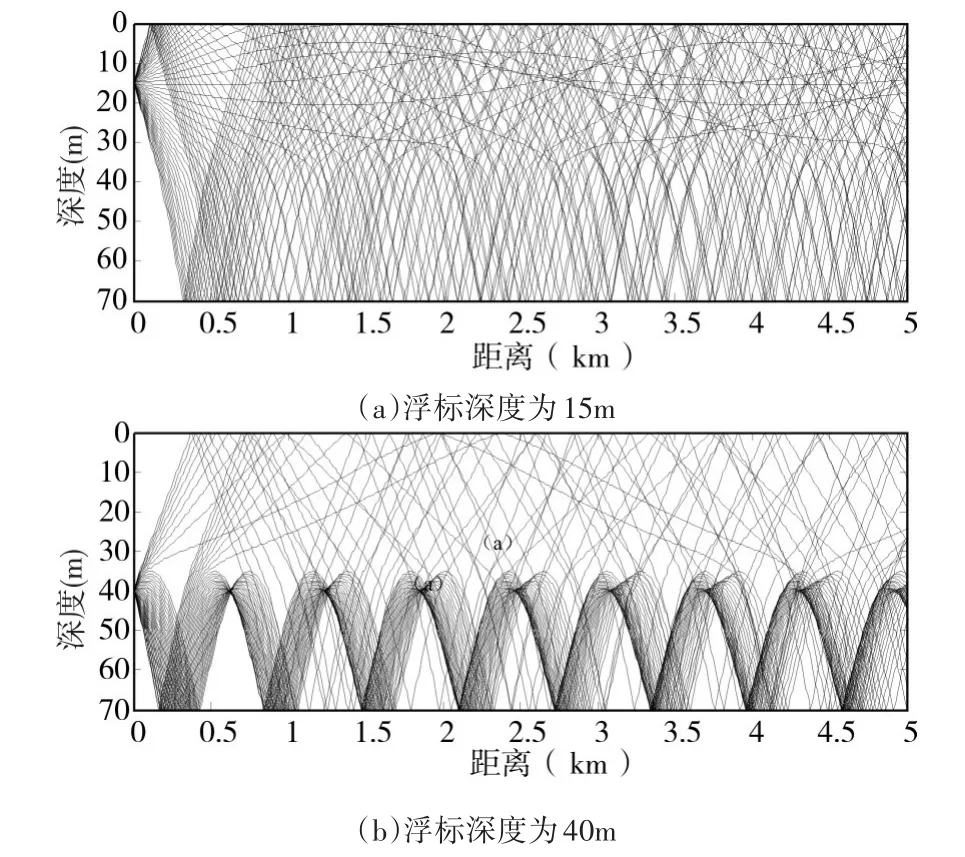
图6 黄海某处11月份声线剖面图

2）图5的声线剖面基本上为均匀分布，声速从海面到海底变化不大，在传播过程中，只有个别声线出现了轻微的弯曲；浮标位于不同深度时，声线图也没有太大的区别。所以，在接近于均匀层的海洋环境中，浮标的工作深度对探测距离基本上没有影响。

3）图6为典型的负跃层情形，在35m～50m左右的海深范围内，海水具有强烈的负梯度，声线在该范围内也产生了明显的弯曲。比较浮标不同的工作深度可以看出：如果潜艇目标位于跃变层以下，那么浮标在跃变层附经的工作深度上可以很容易地发现目标，而如果目标位于跃变层以上，浮标在该深度上却很难发现目标，此时应该将浮标的工作深度也设定在跃变层以上。综合起来，在负跃层的情况下，声纳浮标工作深度的设定要与潜艇目标的可能深度位于跃变层的同一侧。即如果潜艇在50m深度以下时，浮标工作深度设定在40m更容易发现潜艇。

因此，在确定声纳浮标的工作深度时，其基本原则就是应当以实际水文条件的传播损失为依据，根据潜艇目标可能的航行深度，寻找传播损失最小的工作深度。