基于FP-growth的前后部项约束关联规则改进算法∗

李 赞 王朝霞 孟月昊 隋 昊

（陆军勤务学院军事物流系 重庆 401331）

1 引言

关联规则挖掘技术可从海量的数据中发现项之间隐含的、有价值的信息。最典型的算法是Agrawal等提出的 Apriori［1～2］、FP-tree［1～2］算法，但由于在挖掘中没有用户的参与和控制，这些算法会产生大量冗余的频繁项集和无价值的关联规则，使挖掘对于用户的实际需求缺乏针对性，降低了关联规则的使用效率。在实际应用中，用户也希望只挖掘出包含某些项的关联规则，而不是在生成的大量冗余规则中自己去筛选需要的关联规则。比如在工程建设中，监理人员可能只希望了解哪些因素与超投资、超面积有关，而不是泛泛地发现工程建设中所有因素之间的关联规则。这就需要分析者根据用户的具体需求，对事务中的某些项或属性设定约束条件，再进行关联规则挖掘，通过减少冗余规则的产生，来提高用户需找有价值关联规则的效率。对此，许多专家学者展开了基于项约束的关联规则算法研究，并提出了许多有效的项约束关联规则算法。

文献［3～5］提出的经典项约束算法Multiple⁃Joins、Recorder和Direct通过约束条件在挖掘频繁项集过程中进行筛选，减少冗余规则的产生。文献［6～7］提出了将项约束与概念格结合的DFCLA、DFTFH算法，通过格计算较少冗余规则。文献［8～11］提出的这类算法则采用垂直数据形式表示数据集和深度优先的挖掘策略得出项约束关联规则。文献［12］提出了MCAL算法，利用约束条件的单调性及非单调性对项进行筛选挖掘。此外，还有基于项的时序性来进行约束的关联规则算法［13～14］等。

上述基于项约束的关联规则算法大多是从整体的角度出发进行约束，但考虑到用户感兴趣的项应该出现在关联规则的前部还是后部的算法却很少。而用户的需求往往不仅限定了需要挖掘的项，同时也限定了项出现在规则中的位置。这些项约束关联规则算法虽然减少了关联规则的冗余量，但随着事务集的增大，产生的无用关联规则数量仍然较多，仍然存在规则使用效率不高的问题。文献［15］提出的AR_F&R算法虽然提出了前后部项约束关联规则的概念，并给出了相关形式化的定义，但算法基于Apriori，需要多次扫描事务集，计算开销较大。

因此，针对项约束关联规则约束项在规则中的位置不够具体的现状，本文在AR_F&R算法定义的相关概念的基础上，提出了一种基于FP-growth的前后部项约束关联规则算法FRFP（Fore-part and Rear-part FP-Growth）。通过对分别属于前后部的项进行标记，然后筛选压缩事务集，通过简化的FP-tree挖掘出符合约束条件的有效频繁项集和关联规则。实验结果表明，FRFP算法与其他项约束算法相比，生成的关联规则更少，运算性能方面也得到了优化。

2 基本定义

定义 1 设 I=｛I1，…，Ij，…，Ik｝是所有项的集合，其中，Ij为数据项，简称为项（item）。在关联分析中，包含0个或多个项的集合被称为项集（item⁃set）。事务集D是由一系列具有唯一标识的TID的事务T组成，每个事务T包含的项集都是I的子集，即T⊆I。

定义2 形如X→Y的蕴涵式称为一个关联规则，关联规则的支持度Support是事务集D中包含X∪Y的百分比，即 support(X→Y)=P(X∪Y)。Sup_count是指项集X∪Y在事务集D中出现的次数，即支持度计数。若项集的支持度大于等于用户给定的最小支持度minsup（即支持度计数大于等于最小支持度计数min Sup_count），则该项集称为频繁项集。

定义3 关联规则X→Y的置信度Confidence是指事务集D中包含X的事务同时包含Y的百分比，即confidence(X→Y)=P(X|Y)。置信度中的最小值称为最小置信度minconf，一般由用户自己设定。

定义4 规则前部集合F=｛F1，F2，…，Fn｝，该集合描述待挖掘关联规则中用户感兴趣的所有规则前部项的集合，满足 F⊂I且 F≠Φ 。FS=｛FS1，…，FSi，…，FSg｝为F所有非空子集的集合，其中FSj（j=1，2，3…，g）为F的非空子集，称为前部项集。CFj称为前部频繁项集候选项集，大于等于minsup的CFj称为前部频繁项集，记为LFj，LF为前部频繁项集集合。

定义 5 规则后部集合 R=｛R1，R2，…，Rm｝，该集合描述待挖掘关联规则中用户感兴趣的所有规则后部项的集合，满足R⊂I且R≠Φ。RS为R所有非空子集的集合。RS=｛RS1，…，RSt，…，RSn｝，RSt（t=1，2，3…，n）为R的非空子集，称为后部项集。

定义4和定义5隐含以下条件：

条件1 F∩R=Φ。即用户感兴趣的所有规则前部项的集合F与用户感兴趣的所有规则后部项的集合R无交集。

定义6 给定关联规则X→Y，若X⊆F，且Y⊆R，则关联规则X→Y为前后部项约束关联规则。

由条件1得出以下结论：若X→Y为前后部项约束关联规则，则X∩Y=Φ。

证明：F∩R=Φ ，且X⊆F，Y⊆R故 X∩Y=Φ成立。

根据上述相关定义及条件1，进一步提出包含前后部项集的概念。

定义7 给定前后部项集集合IFR=｛IFR1，…，IFRt，…，IFRd｝，则其中的任一项集IFRt（t=1，2，3，…d）是同时包含规则前部项和规则后部项的项集即IFRt⊆(FUR)，且 IFRt∩F≠Φ ，IFRt∩R≠Φ ，IFRt简称为前后部项集。

前后部频繁项集候选项集记为CFRt，若某个项集IFRt大于等于minsup，则称为前后部频繁项集，记为LFRt。包含前后部频繁项集的集合记为LFR。

挖掘用户感兴趣规则前部项和规则后部项的关联规则时，由于原始事务集D的事务中可能有大量冗余项，或者某些事务不包含用户感兴趣的前部项集合或后部项集合，则需要对原始事务集合进行筛选压缩。其依据为

由性质1可得到如下结论：

结论1 给定事务T，∃i：Ii∉T，若Ii∉F且Ii∉R，则从事务T中删除此项。

该结论是删除事务冗余项的依据。

结论2 给定事务T，若T∩F=Φ，则删除此条事务T。

该结论是删除冗余事务的依据。

由 置 信 度 定 义 Confidence(X→Y)=可知，若要求取前后部项约束关联规则X→Y，则必需知道(XUY)和（X）这两种频繁项集的支持度，而X为规则前部，Y为规则后部，则(XUY)表示同时具有规则前部和后部项的频繁项集，故定义前后部项集IFRt及对应的前后部频繁项集LFRt。而（X）表示只具有前部项的频繁项集，故定义前部项集FSj及对应的前部频繁项集LFj。从置信度定义公式可以看出，每个LFRt有且只有一个LFj与之对应，故只能生成一条关联规则，是能够减少冗余规则产生的原因所在。

因此，FRFP算法的思想在于：通过挖掘出所有的前后部频繁项集LFRt和前部频繁项集LFj，来达到求取符合项约束条件的关联规则以及减少关联规则冗余量的目的。整个算法流程均是围绕如何挖掘出所有的LFRt和LFj来进行求解。

3 算法思想及流程

3.1 算法流程

本文提出的FRFP算法流程分为4个步骤，如图1所示。

为更直观形象地理解本算法，以只包含9个事务的事务集D作为案例，如表1左边部分所示，假定用户感兴趣的规则前部集合F=｛I2，I5｝，规则后部集合R=｛I1，I3｝，minsup=0.25。

步骤1 计算频繁1-项集。计算频繁1-项集方法与FP-growth算法相同。频繁1-项集的结果采用表FR-list来描述。表FR-list包括四个域：项名，支持度计数，标记和指针。首先，项按照支持度计数值从大到小排序；标记域用来描述某个项是否属于前部项集合F或后部项集合R，如果该项属于前部项集合，则标记为f，如果该项属于后部项集合，则标记为r；加入指针域则是使得FR-list具有项头表的功能，用于链接后续构建的FP-tree上的节点。

图1 FRFP算法流程图

表1 事务集D及FR-list

对案例事务集D完成步骤1后，生成的FR-list如表1右边部分所示。FR-list的第一列的项按照支持度计数由大到小排序，第二列为项的支持度计数值，第三列存放前部和后部的标记信息，第四列的值暂时为空指针。

步骤2 筛选事务集并建立FP-tree。首先根据结论1和结论2对事务集进行筛选，压缩事务集空间，然后按照FP-growth算法一样建立FP-tree。具体方法见3.2.1节

步骤3 挖掘LFR和LF。在步骤2建立的FP-tree上，挖掘前后部频繁项集和前部频繁项集，并分别放入集合LFR和LF中。本步骤挖掘出所有前后部频繁项集及前部频繁项集，具体方法见3.2.2节。

步骤4 输出关联规则。对于每个LFRt，若存在对应的前部频繁项集LFj，则计算每个前后部频繁项集的置信度Confidence若其置信度大于等于minconf，则输出强关联规则。若不存在对应的前部频繁项集LFj，则不考虑。从而输出所有符合约束条件的关联规则。

3.2 算法具体描述

3.2.1 筛选事务集并建立FP-tree

本节重点阐述对事务集D进行压缩并建立FP-tree的方法。

1）删除事务中的冗余项

分为两种情况：一是删除所有支持度小于minsup的项。二是删除未被标记为f或r的项。以案例事务集合D为例，如图2（c）第三列所示，事务 T200=｛I2，I4｝和事务 T400=｛I2，I1，I4｝中，I4未被标记为f或r，故筛选出I4，并从相应事务中删除。

2）删除冗余事务

根据结论2，去掉只标记有r项的分组事务。而只标记有f项的分组事务，可能会产生前部频繁项集，故保留。以案例事务集合D为例，T500，T700均为｛I1，I3｝，I1和I3均被标记为r，故删除此两条事务。

具体伪代码如下所示：

1.Sort-D（D，FR-list）｛∕删除事务中冗余项，并对事务排序

2.foreach T in D do

3. foreach item in T do

4. if（item.support＜ minsup）or（item未标记为 f或 r）

5.then从T中删除item

6. if T≠Ø then按项支持度值对T中的项降序排列

7.Output Dsorted∕输出排序后的事务集合Dsorted

｝

图2 排序筛选事务集并建立FP-tree

根据筛选排序后的Dsorted建立FP-tree，建树方法与FP-growth算法相同。以案例事务集为例建立FP-tree如图2（c）所示。需要指出的是，为了便于搜索分组FP-tree，以FR-list作为项头表，使前部项和后部项通过指针指向它在FP-tree中的位置。如图2所示，I5为前部项（标记为f），I3为后部项（标记为r），故分别通过指针指向I5和I3在FP-tree中的位置。

3.2.2 挖掘LFR和LF

根据建立的FP-tree挖掘包含前后部频繁项集的集合LFR和前部频繁项集集合LF。具体挖掘方法：1）发现分枝；2）在分枝上挖掘LFR和LF。

1）发现分枝

针对标记为f或r的项，根据每项指针所指位置在FP-tree上找到对应的枝进行挖掘。同时，根据本项在FP-tree上对应的节点的支持度计数来确定分枝上其他节点的支持度计数。如图4所示，以案例事务集合D的FP-tree为例，I5和I3分别标记为f和r。I5通过指针在FP-tree上有两个分支：null→I2：1→I1：1→I5：1 和 null→I2：1→I1：1→I3：1→I5：1。I3在1号分组FP-tree上有两个分支：null→I2：2→I1：2→I3：2，和null→I2：2→I3：2。

2）在分枝上挖掘LFR和LF

若挖掘的是标记为f的项的分枝。例如I5，其生成的频繁项集只可能有两种类型：同时有f和r标记的频繁项集；只有标记为f的频繁项集。而这两类频繁项集又分别属于LFR和LF。故直接按照传统的FP-growth算法，递归挖掘频繁项集即可。

若挖掘的是标记为r的项的分枝。遍历每个分枝，根据FR-list的label中前后部项标记的信息，将分枝上的节点分别放入规则前部集合F和规则后部集合R，并分别求出前部项集集合FS和后部项集集合RS。只保留RS中包含本项的后部项集RSn，然后与FS中的前部项集FSj两两组合连接，生成前后部项集IFRt并输出，但不输出前部项集FSj。如图3所示是挖掘标记为r项的分枝。

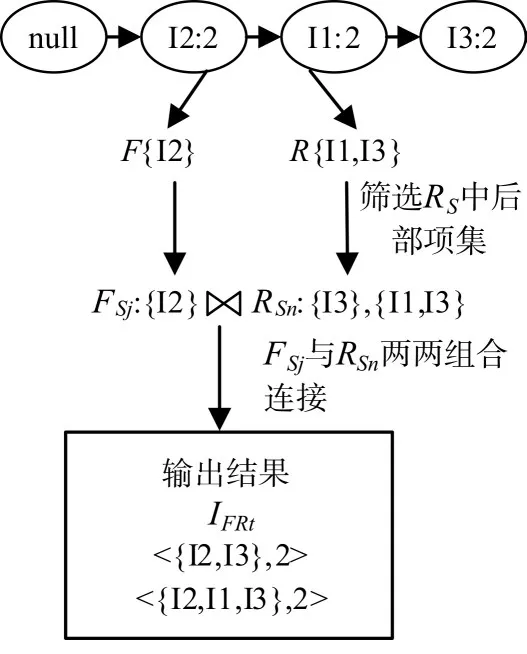
图3 挖掘标记为r项的分支流程图

图4 I5和I3生成的LFR和LF

由图3可知，I3为被标记为r的本分组项。选取I3一条枝null→I2：3→I1：3→I3：3，由于I3出现在规则后部集合R中，故只保留RS中包含I3的后部项集RSn，然后与前部项集FSj两两组合连接，输出前后部项集IFRt。挖掘过程与挖掘标记为f的分组项项基本相同，但不输出FSj。

最后将各分枝挖掘出的IFRt、FSj进行合并，得到候选项集CFRt和CFsj，并根据最小支持度minsup求出前后部频繁项集LFRt和前部频繁项集LFj，并分别放入前后部频繁项集集合LFR和前部频繁项集集合LF中。如图4是标记为f的I5和标记为r的I3生成的前后部频繁项集集合LFR和前部频繁项集集合LF。

由FP-growth算法挖掘频繁项集的方式：以待挖掘项为后缀挖掘FP-tree，构造条件模式树，递归挖掘包含后缀的频繁项集。因此生成的频繁项集必定包含此项，而不包含此项的项集必定不是频繁项集。根据这一特性，在挖掘标记为r的项的分枝时，只保留RS中包含本项的后部项集RSn，以确保挖掘出的有效项集必定是频繁项集。

具体伪代码如下所示：

1.gen-LFR（FP-tree，FR-list，minsup）｛∕发现分枝

2.foreach item in FR-list｛∕对 FR-list中的每项

3.if item.link≠null then

4.branchset←find branch（item.link，FP-tree）；

5. foreach branch in Branchsetdo

6.F←find-Fore-part（branch，FR-list）；

7.R←find-Rear-part（branch，FR-list）；

8.FS←non-empty-powerset（F）；

9.RS←non-empty-powerset（R）；∕挖掘标记为f的项：

10. if item.label=‘f’then∕调用FP-growth算法进行挖掘，挖掘标记为r的项：

12. if item.label=‘r’then∕若本分组项被标记为r，保留RS中包含本分组项的后部项集RSn

14. foreach（FSj∈ FS，RSn∈ RS）do

15. IFRt←FSj▷◁RSn∕生成前后部项集IFRt

∕合并项集生成 LFR，LF

16.CFRt，CFj←aggregate IFRt，FSj∕将相同的 IFRt，FSj进行合并生成候选项集CFRt，CFj

17.foreach CFRt，CFjdo ∕合并同时判断频繁项集

18.if CFRt，CFj≥ min sup×D then

19. LFRt，LFj←CFRt，CFj∕生成频繁项集 LFRt，LFj

20. LFR，LF←add LFRt，LFj∕将 LFRt，LFj添加进 LFR，

LF

21. ｝

22.｝

4 实验结果分析

FRFP算法在MyEclipse开发环境下用Java编程实现，并从不同数据集规模运行时间和生成有效关联规则数比较了FRFP算法与其他项约束算法的优劣，从不同最小支持度运行时间方面分析了FR⁃FP算法本身的性能。实验环境为华硕笔记本，CPU 2.6GHz，4GB内存，操作系统为Windows7。采用的数据集 T40I10D100k 来源于 http：∕fimi.ua.ac.be∕data∕，抽取其中6000条数据作为实验数据。

FRFP与其他算法比较：

1）不同数据集规模运行时间对比。将FRFP算法与 AR_F&R［15］算法、DFTFH［7］算法进行比较，设置最小支持度minsup为10%，最小置信度minconf为50%，如图5所示。

FRFP算法比AR_F&R算法、DFTFH算法在运行相同数据集的条件下，所用时间最少，且随着数据集的增大，运行时间基本呈线性增长，说明FRFP算法的数据规模增长性较好。

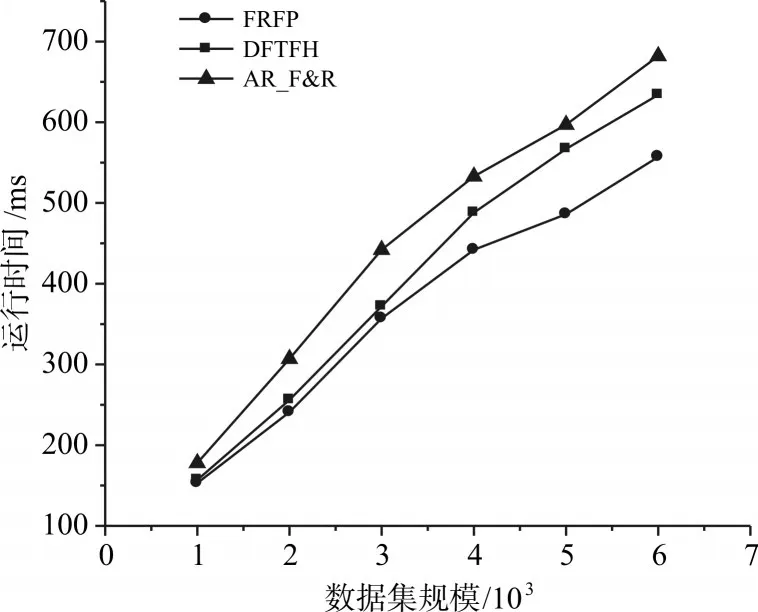
图5 数据集规模运行时间对比

2）生成关联规则数对比。统计实验1中三种算法生成的关联规则数，如下表2所示。

表2 关联规则结果对比

由表2可知，DFTFH算法由于约束条件并未具体约束关联规则前部和后部的项，生成的关联规则数要比有明确前后部项约束的FRFP算法和AR_F&R算法多，而FRFP算法与AR_F&R算法生成的关联规则数基本相同。

FRFP算法自身性能分析：

3）不同最小支持度下运行时间对比。为测试算法在不同最小支持度下运行的时间，选取了最小支持度为0.05，0.1，0.15三种情况进行了测试，测试结果如图6所示。

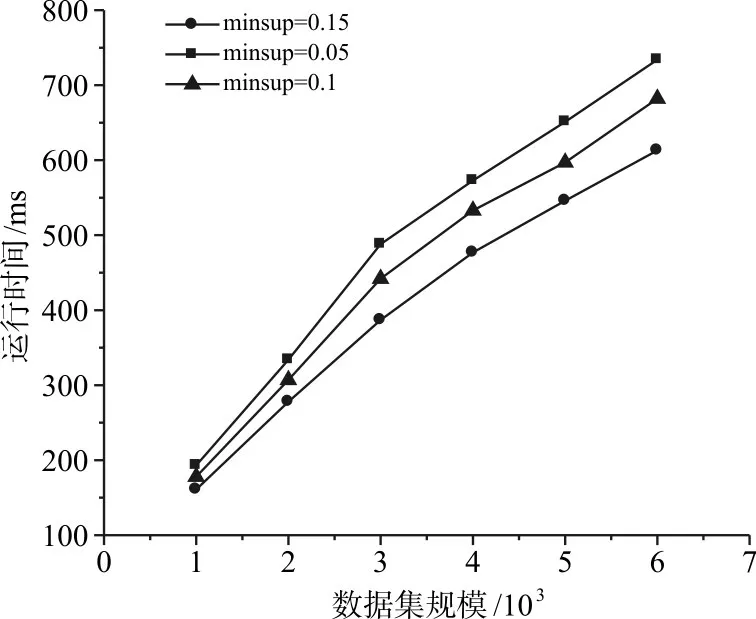
图6 不同最小支持度运行时间

由图6可知，随着最小支持度的增大，FRFP算法运行时间越少，这是由于最小支持度筛选掉了更多的项集，降低了挖掘的复杂程度和计算开销，因此运行时间变少。

5 结语

本文提出的FRFP算法，立足于优化项约束关联规则约束条件不够明确具体的问题，通过对规则前后部具体只出现哪些项进行明确的约束，从而更进一步减少冗余关联规则的产生，满足用户的需求。但FRFP在挖掘实时更新的事务集时，效果欠佳。因此，如何挖掘实时动态更新的事务集将是下一步研究的重点内容。