三相逆变电源解耦控制与输出滤波器设计研究
毕洪大,邹存祚
(中车大连电力牵引研发中心有限公司,辽宁大连116000)
1 引言
三相逆变电源在轨道交通中如地铁、轻轨、高铁动车、磁悬浮、空铁等领域中已被广泛的应用,随着电力机车的不断发展对三相逆变电源的输出电压波形质量的要求也越来越高,即要求三相逆变电源在各种非线性负载下均能实现稳定的正弦电压输出,同时要求动态相应快且输出电压谐波含量小。所以实现高质量电压输出和抑制电压电流谐波仍然是逆变电源设计过程中的核心问题,采用传统的瞬时电压的单环反馈控制的技术,其动态特性和输出性能很难满足需求。
因此,本文通过对三相逆变电源建立了数学模型,在d-q同步旋转坐标系下采用电压和电流双闭环的控制策略,即在设计了电压外环和电流内环反馈控制的同时引入了前馈输出负载电流、前馈输出电压控制,并实现了对耦合关系的变量进行解耦线性控制,系统的动态响应得到很大改善,也提高三相逆变电源的非线性负载的能力,同时提出了后级LC滤波参数的工程设计方法,可以获得较好的三相输出电压波形质量。
2 拓扑结构和模型分析
本文针对电压型两电平桥式逆变电路进行分析,其主电路的拓扑结构如图1所示。
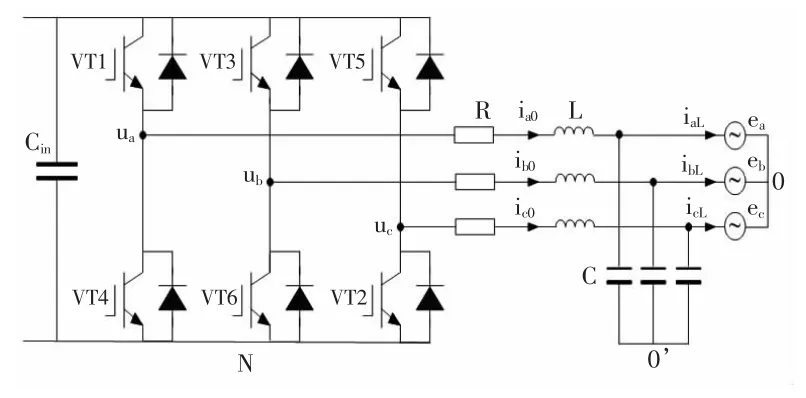
图1 拓扑结构简图
图中:Cin为输入侧支撑电容,LC为输出滤波器,VT1~VT6为IGBT功率开关管,R为等效阻抗。
2.1 d-q同步旋转坐标系下数学模型
在两相d-q两相同步旋转坐标中,电感电流方程如式2所示:

电容电压方程如式4所示:
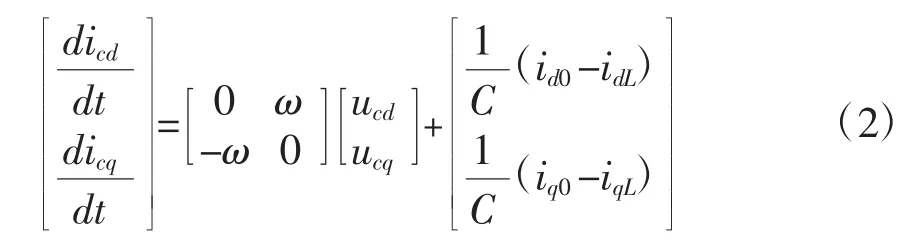
式中idL和iqL分别为d,q轴上电感电流;ucd和ucq分别为d,q轴上电容电压;udc为直流电压;ed和eq为输出电压;id0和iq0为输出电流。
令 sdudc=ud0,squdc=uq0,由式(1)和式(2)可以得到:
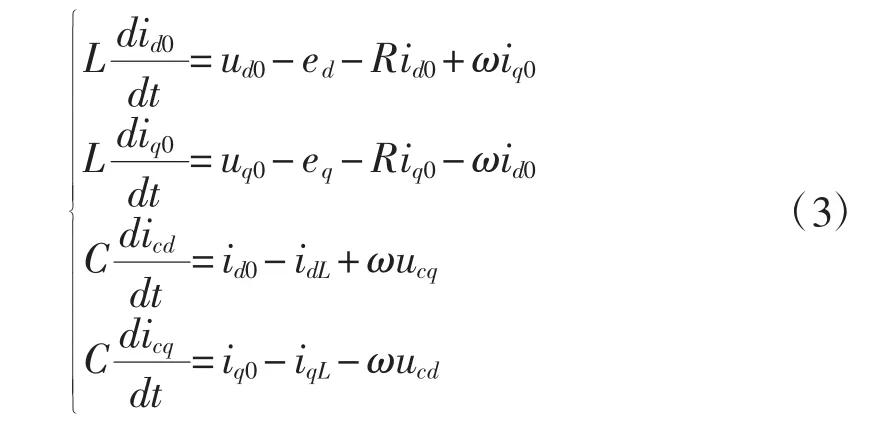
由此可得dq坐标系下模型框图为:

图2 dq坐标系下模型框图
在结合式(3)和模型框图2中,可将ud0和uq0设为逆变电源输出电流id0和iq0的控制量;将id0和iq0作为逆变电源输出电压ucd和ucq的控制量。
2.2 控制系统模型解耦
从三相逆变电源在d-q同步旋转坐标系下的数学模型可以看出,三相逆变电源电源d-q轴的变量之间存在相互耦合的关系,所以,控制系统的设计会存在一定难度,故本文采用在同步旋转d-q坐标系下输出电压和负载电流前馈解耦的双环控制方式实现对控制系统的解耦控制,图3为采用了解耦控制的系统控制框图。
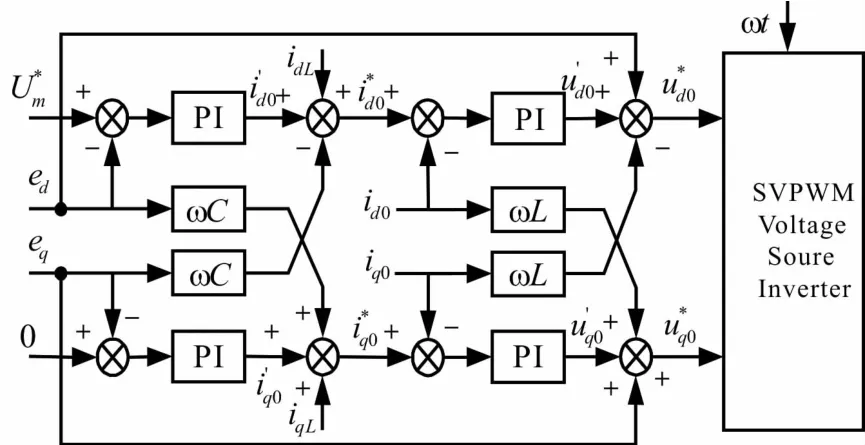
图3 系统控制框图
由式(3)可知,控制变量 ud0、uq0和耦合电压ωLiq0、ωLid0,以及输出电压ed和ed同时对逆变电源d,q轴输出电流id0和iq0产生影响。同理,控制变量系统输出电流 id0、iq0和耦合电流 ωCucq、ωCucd,以及输出负载电流idL和iqL同时影响系统d,q轴输出电压ed和ed。现令:


3 控制系统设计
3.1 双闭环的解耦控制策略
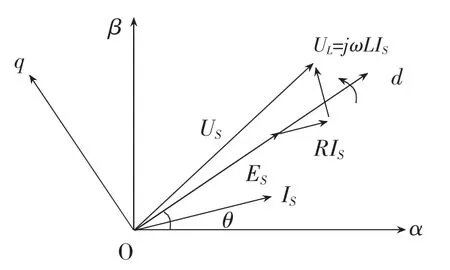
图4 虚拟电网电压矢量定向控制
系统控制框图如图3所示。检测三相负载电压ek,三相负载电流ikL及逆变电源三相输出电流ik0,经C3s/2r坐标变换可以得到对应的d,q轴分量,电压控制器和输出电压反馈构成电压外环(式(5)中的后两式),其输出为电流指令。采用按(虚拟)电网电压矢量定向的控制策略。令输出电压参考指令(输出额定电压峰值),则输出电压稳定控制调节通过外环电压控制器来实现,电流内环的输出作为逆变电源空间电压矢量的输入。由于控制系统引入了负载电流、输出电压前馈量和滤波电容解耦电流、滤波电感解耦电压,三相逆变电源的动态响应速度得到提高,带非线性负载的能力也可以得到提升。此外,本文同时采用SVPWM调制方式,根据电压空间矢量的参考信号,进而产生六路功率开关的驱动脉冲信号,完成对逆变电源的双闭环控制策略。
3.2 LC滤波器参数工程设计
3.2.1 满足电流快速跟踪要求的电感设计
以a相电感电流为例,考虑阻性负载的情况,电流和电压同相位。电流在过零点时变化率最大,故研究零点附近的一个开关周期的电流跟踪瞬态过程,如图5所示。
稳态条件下,当 0≤t≤T1时,使 sa=1,以获得可能的最大,且此时有ea≈0,则:
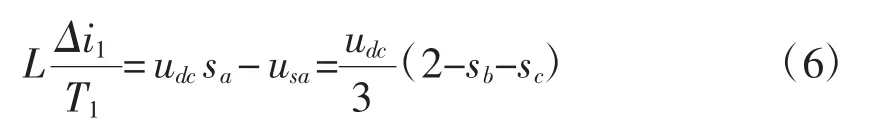
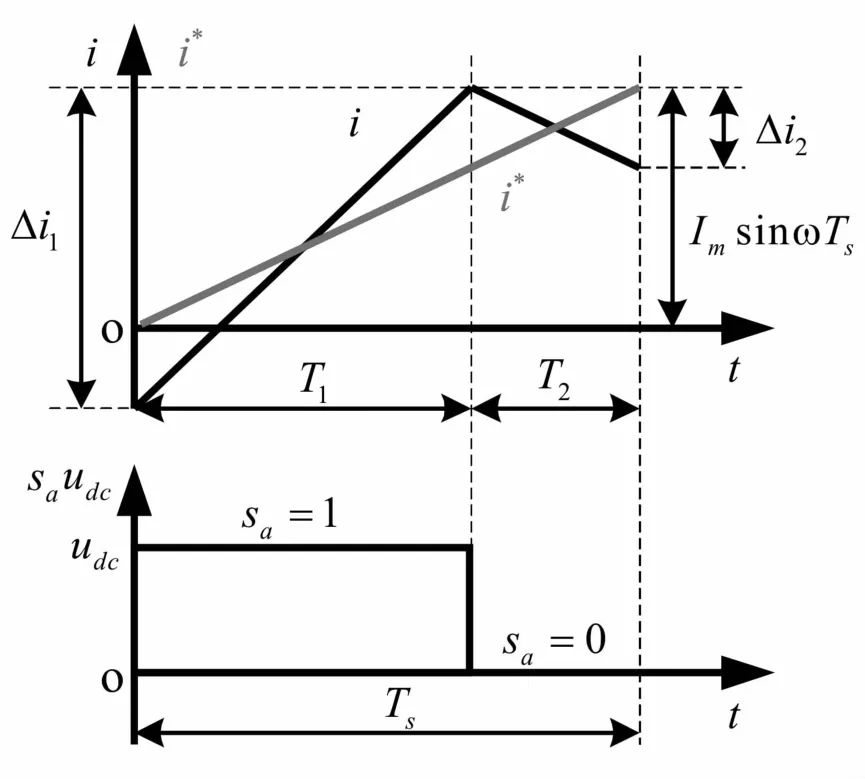
图5 一个开关周期内电感电流曲线
图5电流过零点附近的一个PWM周期
当T1≤t≤Ts时,sa=0,此时仍有 ea≈0,则:

若满足电流快速跟踪要求,则必须
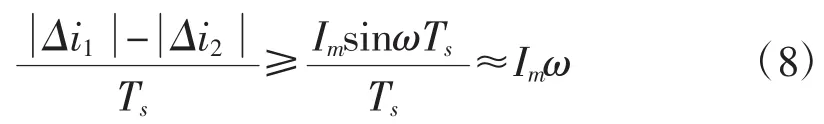
并假设 sb=sc=0,以使得分别对应式(7)和式(8),表示功率开关管导通时电流上升率快,关断时电流变化小,则有:

当T1=Ts时,将取得最大电流变化率,且

3.2.2 谐波抑制的要求
为抑制谐波电流,电感应足够大。谐波电流脉动最严重情况发生在正弦波电流的峰值附近(以SPWM为例,因为在此附近,脉宽最大),如图5所示,故我们可研究在发生在电流峰值附近一个PWM开关周期一个开关周期内电感电流曲线的瞬态过程。
稳态条件下,当 0≤t≤T1时,使 sa=1,以获得可能的最大,且此时有ea≈Em,则:

当 T1≤t≤Ts时,sa=0,此时仍有 ea≈Em,则:
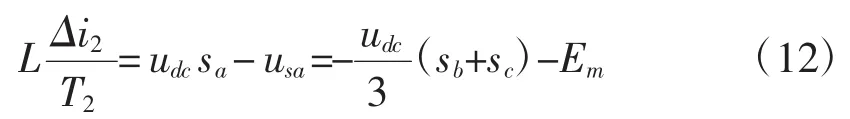

图6 电流峰值附近的一个PWM周期

假设谐波电流脉动幅值最大允许为Δimax,则有:
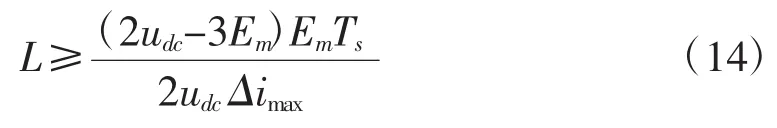
故在满足电流瞬态跟踪和谐波抑制约束下的电感L取值范围为:

若上式成立,则电感L上、下限比值λ必须满足:
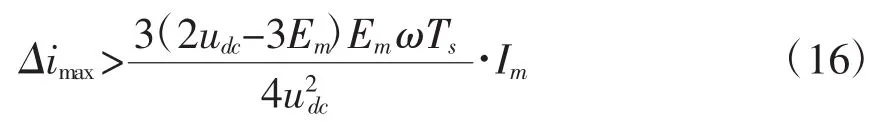
3.2.3 LC滤波器综合
如图7所示的LC滤波器,其输入输出关系为:

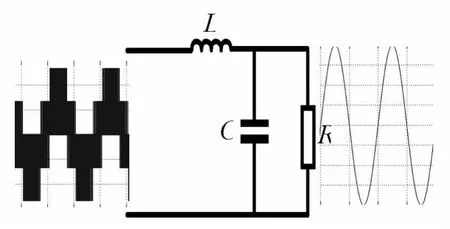
图7 逆变电源输出LC滤波器
影响滤波效果的参数主要是转角频率ωn和阻尼比ξ。为了实现对开关频率及其附近频带的谐波进行抑制,选择逆变电源输出LC滤波器的转折频率为要远低于开关频率fs,通常取fn≤fs/10,即

综合2.2.1-2.2.2节的结论,概括设计步骤如下:STEP1:确定系统的开关周期T(s频率f)s、逆变电源输出电压频率ω、输出电压峰值Em,输出电流峰值Im以及直流测电压udc;
STEP2:利用式(16)确定下系统允许的Δimax;
STEP3:利用式(15)确定滤波电感参数L;
STEP4:利用式(18)确定滤波电容参数C。
另外,电容值越大,产生的无功越多,造成系统效率降低。一般电容产生的无功被限制为不超过5%的系统额定功率,即

4 试验验证
4.1 系统参数
搭建应用于轨道车辆的40kVA三相辅助逆变器电源样机,其基本参数如表1所示。

表1 三相逆变电源基本参数
4.2 仿真及试验验证
利用Matlab Simulink仿真软件搭建带前馈解耦的双闭环控制策略仿真试验模型如图8所示。
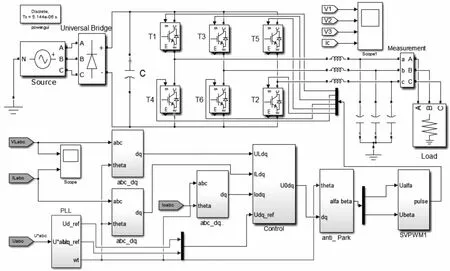
图8 系统控制仿真模型
解耦控制模块(Control)的内部仿真控制模型如图9所示。
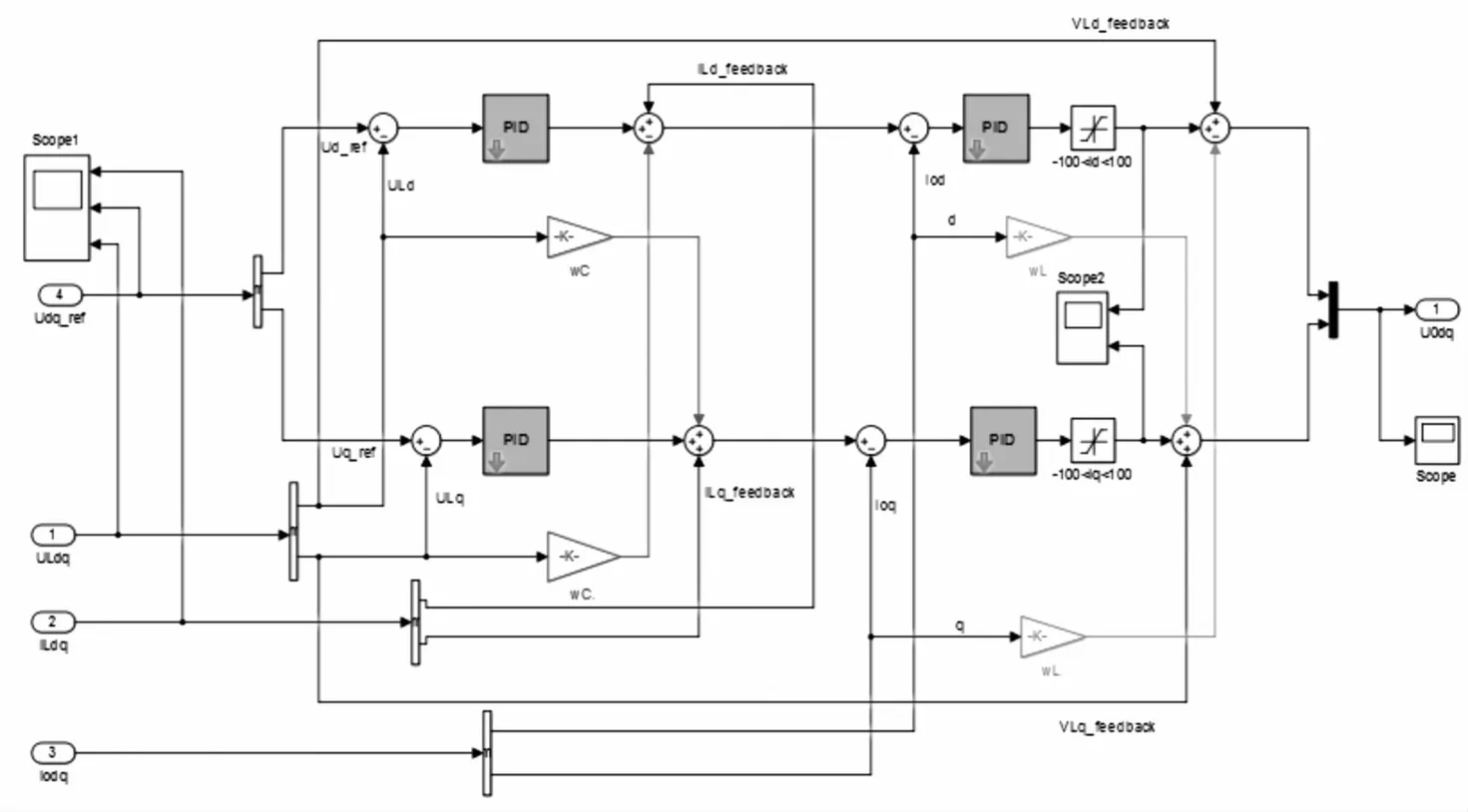
图9 解耦控制仿真模型
采用输出电压和负载电流前馈解耦的双环控制系统,系统分别在0.16s时突加20kVA负载,0.42s时突减20kVA负载,三相电压电流仿真波形如图10所示。

图10 突加、突减负载仿真波形
从仿真波形可以看出带前馈解耦的双闭环控制策略,突加、突卸负载时系统具有较好的动态特性。如图11所示,在40kVA三相辅助逆变电源样机上对系统控制策略设计方法的准确性做了进一步试验验证。
5 结束语
对于三相逆变电源的的设计来说,其关键问题是要如何能够增强系统的动态电压响应能力和输出电压波形质量。本文通过建立三相逆变电源的数学模型,分析了在同步旋转坐标系下的各变量间的关系,并引入了一种待输出电压和负载电流前馈解耦的双环控制策略,其实现了对三相逆变电源的线性解耦控制。该控制策略控制简单可靠,参数选取和整定方便,可改善系统的动态响应,提高三相逆变电源的非线性负载的能力。同时还提出了后级LC滤波参数的工程设计方法,三相输出电压波形质量得到明显提升,本工程设计实用性强,适用于各种三相逆变电源的设计中。通过研制应用于轨道交通车辆的40 kVA三相辅助逆变电源样机对本文提出的控制策略和工程设计方法进行了试验验证。

图11 40kVA样机试验波形

