不规则场地铺砖的优化设计——以南昌站站台为例

范信顺 江西省九江市工程造价管理站，九江 332000

南昌站是京九线在中部地区的省会站，又是浙赣铁路的交汇处，客流量大，位于南昌市中心。既有车站为线侧平式，高架候车室跨线进站，旅客地道出站站场既有4座站台。本次施工为新老站房连接与新建城际场二台三线，东站房及站台处高架候车室，同时新建无站台柱雨棚及14米宽旅客出站地道，新建11、12、13道及 五、六台，改造一～四台及南北头咽喉区道岔与相关线路。总建筑面积为84713m2，其中新建东站房18458m2，新建高架候车室16540m2，新建无柱雨棚49715m2。

南昌站采用了国内外少见的大曲率站台，场地狭小，不规则弧形站台多，同时站台面标准高，要求美观圆滑，不能做成锯齿或者折线形，这给大曲率站台石材铺贴及对应的大曲率雨棚钢结构安装精度控制带来了很大的难度。

1 最小包络矩形算法——减少废砖数量

目前，国内外对铺砖方案的研究更多是施工工艺方面，而对铺砖优化设计的研究十分稀少，往往都是依靠技术工人的熟练程度和经验总结。但是这种方法不仅耗费人力，而且会造成大量的废砖。根据南昌站改建工程的施工背景和施工要求，对南昌站的多个不规则弧形站台地面进行铺砖优化设计，并根据优化算法生成铺砖效果示意图。针对南昌站大曲率站台的实际情况和铺砖的工艺要求，拟通过曲线拟合、图形分析和优化分割等方法解决南昌站异形界面优化铺砖的关键问题，在符合施工要求的情况下尽可能减少用砖数量，降低成本。

（1）基于最小二乘法的直线拟合

曲线拟合是一种广泛应用于工程实测数据和科学实验数据的处理方法，它利用连续曲线近似地刻画平面上离散点组所表示的函数关系从而分析数据。通过对曲线的相关特征参数的分析研究，为实验数据寻求最佳拟合曲线，试图找到数据内在的规律。为解决南昌站站台不规则弧形边界的处理问题，通过最小二乘法将边界曲线拟合为直线处理，并将站台平面构成几何多边形处理。利用最小二乘法可以简便地求得未知的数据，最小二乘法还可用于线性拟合。在本项目中，首先需要对站台的弧形边界进行直线拟合，在CAD中导出站台平面图后选取一些切点作为关键点，可通过C++实现直线拟合。

（2）不规则多边形的最小包络矩形的构造

多边形的最小包络矩形是指能完全包含多边形上的所有顶点，且各边均与多边形相接触，在多边形的无数外接包络矩形中面积最小的一个包络矩形。在求取不规则多边形最小包络矩形时，一般可以分为凹多边形和凸多边形分别求解，首先判断出该多边形的内角大小和各顶点的凹凸性，若是凹边形则首先需补为凸边形再对其进行求解，然后根据最小包络矩形的旋转角度分割所需要的网栅进行求取（例如方砖规格600mm×600mm，即为网栅规格）。

（3）多边形的内角和凹凸性判断

通过多边形面积求解公式来进行多边形各顶角的凹凸性的判断，通过DXF得到各顶点坐标，若多边形的顶点坐标（x1，y1）（x2，y2）......（xn，yn）按照逆时针排列，则该多边形面积表示为：

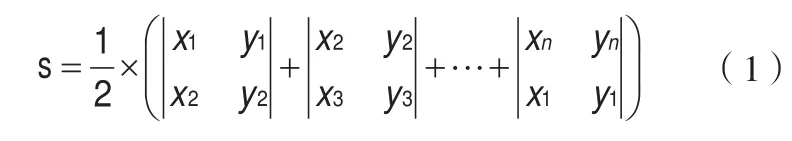
设多边形的顶点是按逆时针排列的，按顺序获取三个顶点i-1，i，i+1，根据面积计算公式（2）求取三个顶点的面积ΔS：

这时ΔS＞0，且i点是凸顶点；如果ΔS＜0，三个点是顺时针排列的，则i点是凹顶点；如果ΔS＝0，则i点与i-1和i+1三点共线。通过多边形连续的三个顶点，以及点线之间的关系就可以确定中间顶点的内角角度，但是求解过程中会出现两个值，为了确定每个内角的角度（假设为A），这里要加入顶点凹凸性来进行判断。如果该顶角是凸角，则其内角0°＜A＜180°；反之，其内角180°＜A≤360°。

以上是对各顶角的凹凸性进行判断，在工程中，也可以采用叉积法进行多边形凹凸性的判断，其中主要是应用到向量叉乘，判断依据为：将多边形边长用向量进行表示，并将相邻边长进行向量叉乘，若所有叉积均为负或均为正，则该多边形为凸多边形，反之，则为凹多边形。如图1所示。

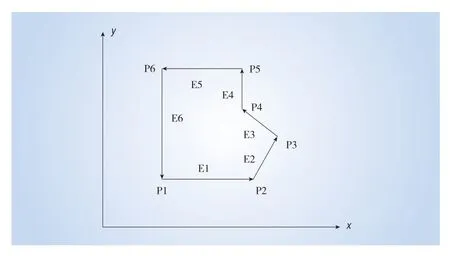
图1 凹凸性判断

（4）凹多边形的凸化处理（凸包法）

如果一个多边形的每一个顶点都是凸的，那我们就将这个多边形定义为凸多边形；只要多边形有一个顶点不是凸的，即为凹多边形。目前，判断多边形顶点凹凸性的算法有多种，常用的有凸包算法、矢量面积法、角度法、向量积法等，本文采用凸包算法进行执行，执行过程主要包括排序、准备堆栈、反复退栈、求出凸包四个步骤，总之，凸包法的主要原理就是先找出多边形中内角度大于180°的顶点，标记为凹点，然后将顶点相邻的两个点连接，遮挡凹陷的区域，重复上述步骤直至所有凹点去除，从而达到多边形凸化的目的。

（5）求解最小包络矩形

①包络矩形算法概念

最小包络矩形算法可以对二维不规则图形进行简化预处理。该算法的思想是在排样初期，根据图形形状特征进行相应的处理，使之构成近似矩形且尽可能紧密排列，从而获取最终的排样图案。该算法较为简单便捷，但是如果一旦忽略了图形的形状特征，就会极大降低图形的利用率，因此在确定最小包络矩形时，应将不规则图形的形状考虑进去。

最早是利用穷举法来求取最小包络矩形，就是通过对所有包络矩形进行筛选，找到面积最小的包络矩形。但是这种算法存在一定的缺陷，不仅计算量大，速度慢，而且需要在一定限定的条件下才可能得到最小包络矩形。该方法的主要步骤是：先对凹多边形进行凸化处理，求出凸多边形边长与坐标轴的夹角；再以凸多边形的边长为基准，对其进行旋转、选择，使得这条基准边长与某一坐标轴重合，得到一个新的凸多边形；最后求出包络矩形的面积，其中，面积最小的包络矩形就是最小包络矩形。

②最小包络矩形排样问题的研究

由于二维矩形件优化排样难，目前还未找到有效解决排样问题的通用算法。在南昌站站台铺设面砖时，对其定向一次性填充到底，尽量减少对砖块的切割次数，其填充工艺描述如下：设已知站台的长为L，宽W（L≥W），所需砖块的尺寸为600mm×600mm。优化排样的基本目标：待铺设的面砖在满足站台铺设面上互不超越不重叠站台边界的前提下，不仅能快速重复进行填充，而且提高砖块的利用率。将排样布局砖块的利用率定义为Emax，利用率越大，砖块的切割次数越少，砖块的利用率就越高。排样模型如下：首先，实现矩形件排样的关键在于排放算法。在满足任何一个待排放矩形在不超越材料的情况下，同时满足BL（Bottom-Left）算法。其次，现场施工最重要的规则是：先角后边。事实上，据观察和了解，一般在填充面砖时，工人总是拉一根水平线，然后从水平线一边开始向另一边进行填充。

以上排样方案中，满足了“一填到底”的铺砖工艺要求。由于只讨论了板材的宽W对待铺设面砖长或宽求余的结果，对于铺设面砖后剩余的板材边界面积，也可考虑其对面砖长或宽的求余结果。两者可以同时进行，再根据最后结果排样。其目的是使不能填充的部分的面积达到最小，以此提高材料的利用率。

2 大曲率站台算法具体设计

（1）具体步骤

步骤1：首先要导入站台的CAD设计图，并进行图形预处理。

步骤2：显示出站台的缩放图像，并在右下角注明缩放比例。

步骤3：对站台的大曲率不规则图形进行直线拟合，从而得到多边形。

步骤4：对拟合后的多边形按照几何特征分类，主要为类平行四边形和类梭形。

步骤5：选择基于几何特征的分割算法。

步骤6：判断是否为类平行四边形，若是，则按照铺砖的规格进行最小包络矩形的分割，否则，进行下一步判断。

步骤7：判断是否为类梭形，在多个类梭形的情况下考虑组合。

步骤8：对最终分割出的结果进行用砖数量计算，切割次数计算等，得出评价结果。

（2）实际效果展示

在阐述了直线拟合和求取最小包络矩形的方法后，可将南昌站站台划分为多个部分，分别求取各个部分的最小包络矩形，并按照矩形的旋转角度分割600mm×600mm的网栅，即为铺砖效果图。在分析了南昌站站台后可归纳出两种典型的铺砖界面，分别是类平行四边形和类梭形。图2为原图的铺砖效果局部示意图，图3为改进后的铺砖方案后的局部示意图。

（3）类平行四边形铺砖界面

以南昌站六站台类平行四边形部分（如图2所示）为例，求其最小包络矩形。

按照上述七个步骤求取最小包络矩形：在最小包络矩形中均匀分割网栅，生成改进后的铺砖效果示意图，如图3所示。

图2 原南昌站六站台局部铺砖示意图

图3 改进后的南昌站六站台 局部铺砖示意图

3 对比与总结

在CAD中导出铺砖效果图后，通过分布式网栅计算可得到同面积同几何边界情况下改进铺砖方案前后所用砖数量和切割次数的多少。用砖数量越少，工程成本越低；切割次数越少，操作复杂度越小。

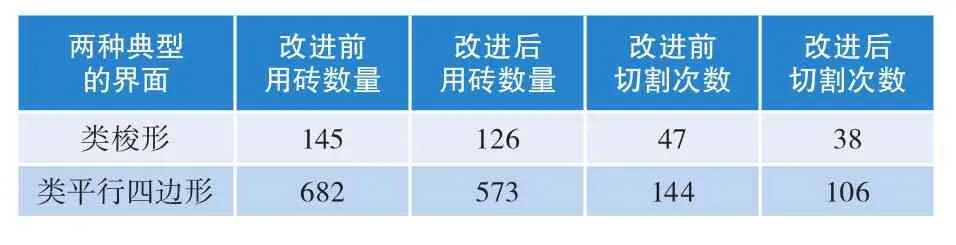
同面积同几何边界情况下改进铺砖算法前后的用砖数量和切割次数

①运用CAD对南昌站大曲率站台边界平面图进行导出，对平面图进行直线拟合和多边形的构造。

②Matlab软件对多边形进行矩形分割和最小包络矩形的求解，生成利于铺砖的规则矩形。

③根据待铺砖的规格对各部分矩形进行网栅分割处理，最终生成铺砖方案示意图。

通过解决关键技术进一步改进任意多边形的分割方案并扩充其使用范围，对类似工程的设计与施工具有指导意义。