The influence of Thomson effect and inclined loads in an electro-magneto-thermoelastic solid with voids under green–Naghdi theories

Elsayed M. Abd-Elaziz , Mohamed I.M. Hilal

Department of Mathematics, Zagazig University, Faculty of Science, P.O. Box 44519, Zagazig, Egypt

Abstract The present investigation deals with the 2-dimensional deformation in a homogeneous thermoelastic solid with voids subjected to inclined loads. The heat conduction equation is affected with the Thomson coefficient. The basic governing equations are modified by using Green–Naghdi theory of type-III. The normal mode analysis technique is used to obtain the components of stress, strain, temperature, induced magnetic field and change in volume fraction field. The variations of these quantities have been depicted graphically in the Green–Naghdi theories of type-II and III for an insulated boundary. From numerical calculations, the effect of Thomson parameter and angle of inclination on a homogeneous, isotropic, electro-magneto-thermoelastic material with voids is revealed and discussed.

Keywords: Electro-magneto-thermoelasticity; Normal mode method; Inclined loads; Voids; Thomson effect; Green-Naghdi theory.

1.Introduction

The generalized thermoelasticity theories have been developed with the aim of removing the paradox of infinite speed of heat propagation inherent in the classical coupled dynamical thermoelasticity theory investigated by Biot [1] .In the generalized theories, the governing equations involve thermal relaxation times and they are of hyperbolic type.The extended thermoelasticity theory by Lord and Shulman[2] which introduces one relaxation time in the thermoelastic process and the temperature-rate-dependent theory of thermoelasticity by Green and Lindsay [3] , which takes into account two relaxation times, are two well established generalized theories of thermoelasticity. Green and Naghdi[4–6] developed a generalized theory of thermoelasticity which involves thermal displacement gradient as one of the constitutive variables in contrast to the classical coupled thermoelasticity which includes temperature gradient as one of the constitutive variables. An important feature of this theory is that it does not accommodate dissipation of thermal energy.On this theory the characterization of material response to a thermal phenomenon is based on three types of constitutive response functions. The nature of those three types of constitutive response functions is such that when the respective theories are linearized, type I is same as classical heat conduction equation (based on Fourier’s law), whereas type II,the internal rate of production of entropy is taken to be identically zero, implying no dissipation of thermal energy. This model is known as the theory of thermoelasticity without energy dissipation. Type III involves the previous two models as special cases, and admits dissipation of energy in general, in this model, introducing the temperature gradient and thermal displacement gradient as the constitutive variables. Sharma and Chauhan [7] investigated a problem concerning thermoelastic interactions without energy dissipation due to body forces and heat sources. Marin et al. [8] discussed a modeling of microstretch thermoelastic body with two temperatures. On temporal behavior of solutions in thermoelasticity of porous micropolar bodies has been adopted by Marin and Florea [9] .

Theory of linear elastic materials with voids is an important development of the classical theory of elasticity, this theory deals with the materials which having the distribution of small (porous) or voids, where the volume of void is included among the kinematics variables and investigate various types of geological and biological materials since the classical theory of elasticity is not sufficient. The theory reduces to the classical theory when the volume of the void tending to zero. Non-linear theory of elastic materials with voids was established by Nunziato and Cowin [10] . Cowin and Nunziato[11] developed a theory of linear elastic materials with voids to study in a mathematical model the mechanical behavior of porous solids. Puri and Cowin [12] studied the behavior of plane waves in the linear elastic material with voids. Iesan[13] developed the linear theory of thermoelastic materials with voids. Cicco and Diaco [14] discussed a theory of thermoelastic materials with voids and without energy dissipation.

The study of dynamic response of an isotropic generalized thermoelastic solid with additional parameters is helpful in solving many practical problems. Initial stresses are developed in the medium due to many reasons, resulting from difference of temperature, process of quenching, gravity variations, etc.The earth is supposed to be under high initial stresses. It is therefore of great interest to study the effect of these stresses on the mechanical and thermal state of the medium. Montanaro [15] investigated isotropic linear thermoelasticity with hydrostatic initial stress. Othman and Abd-Elaziz [16] studied the effect of thermal loading due to laser pulse on generalized thermoelastic medium with voids under dual phase lag model.Othman et al. [17] investigated the effect of initial stress on a thermoelastic medium with voids and microtemperatures.

The study of electro-magneto-thermoelastic interactions which deals with the interactions among strain, temperature,and electromagnetic fields in a thermoelastic material, is of great practical importance due to its extensive uses in diverse fields, such as geophysics (for understanding the effect of the Earth’s magnetic field on seismic waves), damping of acoustic waves in a magnetic field, designing machine elements like heat exchangers, boiler tubes where temperature-induced elastic deformation occurs, biomedical engineering (problems involving thermal stress), emissions of electromagnetic radiations from nuclear devices, development of a highly sensitive superconducting magnetometer, electrical power engineering,plasma physics, etc. [18 , 19] . Kaliski and Nowacki [20] investigated the magneto-thermoelastic disturbances generated by a thermal shock in an elastic half-space having a finite conductivity. Ezzat and El-Karamany [21] solved a two-dimensional problem in magneto-thermoelasticity with two relaxation times in a conducting medium with variable electrical and thermal conductivity by Laplace and Fourier transforms.Othman et al. [22 , 23] have studied much interest applications dealing of magnetic field with thermoelasticity. Effect of rotation and gravitational on a micropolar magneto-thermoelastic medium with Dual-phase-lag model has been investigated by Othman and Abd-Elaziz [24] . Bhatti et al. [25] investigated the electromagnetohydrodynamic (EMHD) flow with heat transfer on third-grade fluid containing small particles. Bhatti et al. [26] studied the heat and mass transfer with the transverse magnetic field on peristaltic motion of two-phase flow (particle-fluid suspension) through a planar channel.Ellahi et al. [27] investigated the effects of nano-ferroliquid under the influence of low oscillating over stretchable rotating disk. Hussain et al. [28] studied the multiphase fluid flow under the influence of electro-magnetohydrodynamics(EHD). Bhatti et al. [29] investigated the combined effects of heat and mass transfer on the peristaltic propulsion of two-phase fluid flow through a Darcy-Brinkman-Forchheimer porous medium with compliant walls.

Fig. 1. The inclined normal and tangential loadings over a thermoelastic half-space with voids.

The present investigation is aimed at the study of the general plane strain problem of generalized electro-magnetothermoelastic half-space solid with voids subjected to inclined loads and Thomson effect. The model is illustrated in the context of the Green–Naghdi theory of thermoelasticity. The Thomson coefficient assumed to be a constant but the charge density of the induced electric current considered as a function of time. Normal mode technique is used for finding the expressions for the variables considered. The distributions of considered variables are represented graphically.

2.Formulation of the problem and governing equations

We consider a homogeneous, isotropic, thermoelastic material with voids in the un-deformed temperature,T0with a half space (y≥0). The rectangular Cartesian coordinates system (x,y,z) have originated on the surface (z= 0).Suppose that an inclined line loadF0per unit length is acting on thez− axis and its inclination toy− axis is θ( Fig. 1 ). For two dimensional problem we assume the dynamic displacement vector as u = (u,v, 0) . All quantities considered will be a function of the time variablet, and of the coordinatesxandy. A magnetic field with constant intensity,namely H = (0, 0,H3) , acts parallel to the bounding plane(taken as the direction of thez- axis. The magnetic field H = (0, 0,H0+h(x,y,t)) produces an induced magnetic field h and an induced electric field E = (E1,E2, 0) , which satisfy the linearized equations of electro-magnetism.

The variation of electric and magnetic fields inside the medium are given by Maxwell’s equations [30] as follows:

The above system of coupled equations are supplemented by the modified Ohm’s law for a medium with finite conductivity [31] , namely

The constitutive relations in a homogeneous, isotropic thermoelastic solid with voids [10] can be written as:

where theviis the components of the velocity of the charges.

Now, we consider the charge density is function only in time, thus Eq. (14) will take the form

If we consider that, the velocity of the chargesviis proportional to the velocity of the particlesu˙i, we can set that

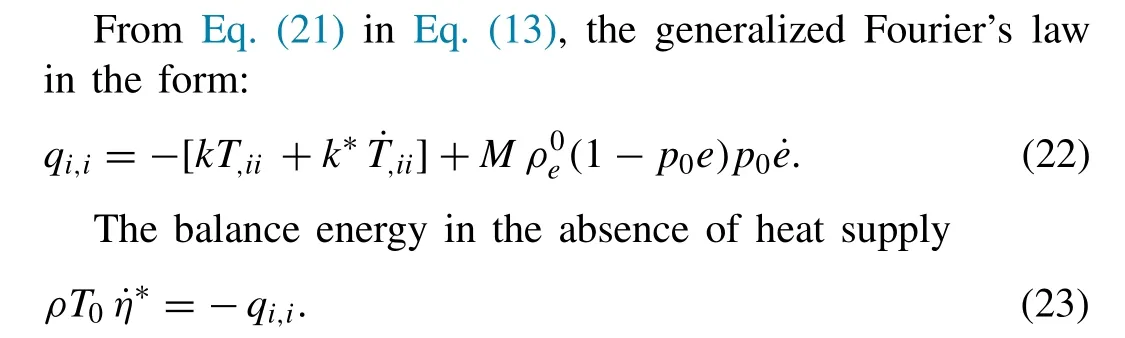
From Eqs. (9) and ( 22 ) into Eq. (23) , we get, the heat conduction equation in the context of Green–Naghdi(G-N)theory, in the form

Sincep0is small non-dimensional constant, we can approximate the above equation to the following form

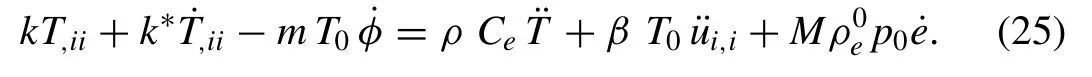
In the above equations a dot denotes differentiation with respect to time.

Hence, from Eqs. (6) and ( 10 ), we obtain the stress components in the form:

The equations of motion, taking into account the Lorentz force

The Lorentz force is given by

The current density vector J is parallel to electric intensity vector E , thus J = (J1,J2, 0) .

The Ohm’s law (5) after linearization gives

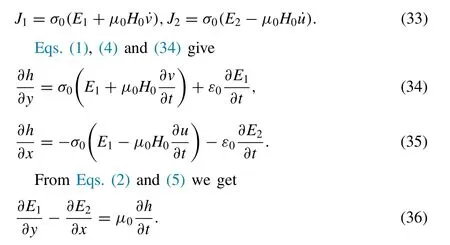
3.The solution of the problem

We define the dimensionless quantities

In terms of the non-dimensional quantities defined in Eq. (44) , the above governing equations reduce to (dropping the dashed for convenience)

Differentiating Eq. (45) with respect tox, and Eq. (46)with respect toy, and then sum, we obtain

Differentiating Eq. (49) with respect toy, and Eq. (50) with respect tox, and then sum, we obtain

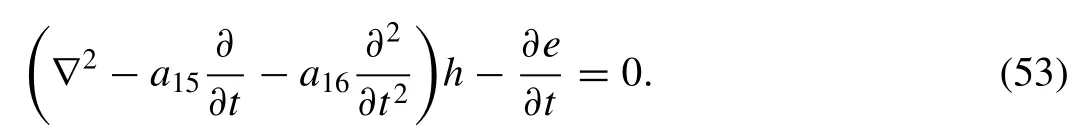
The solution of the considered physical variables can be decomposed in terms of normal mode analysis in the following form

The system of Eqs. (55) –( 58 ) has a nontrivial solution if the determinant of coefficient of ( φ∗,e∗,T∗,h∗) vanishes.After solving these equations we obtain a biquadratic equation of the form

4.Boundary conditions

In order to determine the constantsR1,R2,R3andR4,we need to consider the following boundary conditions at the surfacesy= 0,

4.1. The normal stress condition (mechanically stressed by constant force), so that

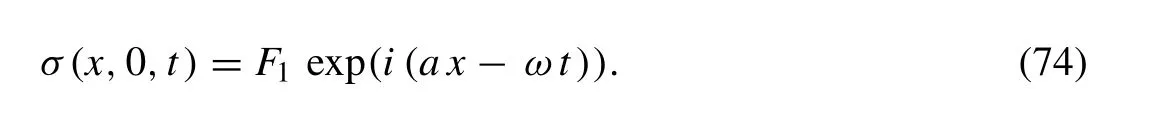
4.2. The tangential stress condition (mechanically stressed by constant force), so that

whereF1andF2are the magnitudes of force and for an inclined loadF0, per unit length, we haveF1=F0cos (θ) ,F2=F0sin (θ) .

4.3. The thermal boundary condition

We will consider the bounding plane of the medium is thermally shocked by the function

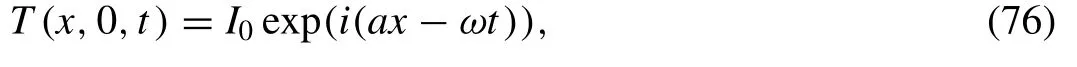
whereI0is constant.

4.4. The electromagnetic boundary condition

The transverse components of the magnetic field intensity are continuous across the surface of the half space,h(x, 0,t) =h∗, whereh∗is the magnetic intensity in free space. We will consider the free space bounding the medium has no any magnetic or electrical field, which mean that

Using the required expressions of the variables into the above boundary conditions along with non-dimensional quantitiesand applying normal mode analysis, we obtain the following system of equations (after suppressing the primes)

They may be written in the matrix form

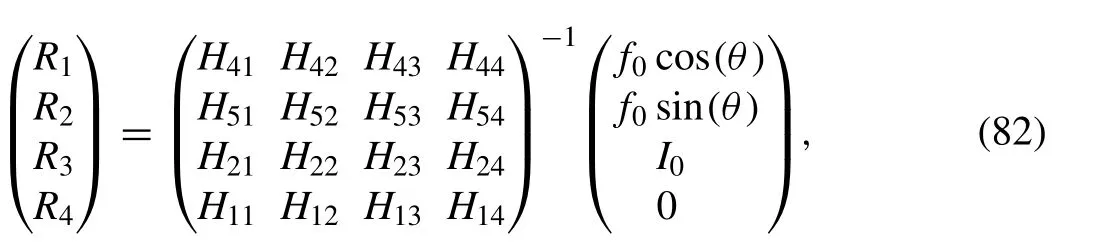
which gives values of the four constantsRn(n= 1 , 2, 3 , 4) .Therefore, the physical quantities of the medium will be fully determined.

Fig. 2. The induced magnetic field h distribution at H 0 = 10 5 and θ= 0.

Fig. 3. The strain e distribution at H 0 = 10 5 and θ= 0.

5.Numerical results and discussion

For numerical computations, following Dhaliwal and Singh[32] magnesium material was chosen for purposes of numerical evaluations. All the units of parameters used in the calculation are given in SI units. The constants were taken as

Fig. 5. The stress σ distribution at H 0 = 10 5 and θ= 0.

Fig. 6. The tangential stress σ xy distribution at H 0 = 10 5 and θ= 0.

The voids parameters are

Since, we have exp (ωt) = [ cos ( χ1t) +isin ( χ1t)] exp ( χ0t)and for small values of time we can take ω = χ0(real).

The comparisons have established for two cases in the context of two theories namely: G-N theory of type II and G-N theory of type III.

Case 1: Different values of Thomson parameterM0[M0=0, 0. 2and0. 5at: θ= 0].

Case 2: Different values of inclination θ [ θ= 0,45and90at:M0= 0].

Case 1: In the Figs. 2 –7 , the computations were carried out forM0= 0. 0, 0. 2and 0.5 at θ= 0,x= 0. 2,H0= 105andt= 0. 1 . The induced magnetic fieldh, the straine, the temperatureT, the stresses σ , σxyand the change in the volume fraction field φdistributions are represented graphically in two dimensional graphs at diffrents position ofywhere the solid lines represent results for the G-N theory of type II atM0= 0, the small dashes line represent results for the G-N theory of type III atM0= 0, the small dashes line with star represent results for the G-N theory of type II atM0= 0. 2,the small dashes line with plus represent results for the G-N theory of type III atM0= 0. 2, the large dashes line represent results for the G-N theory of type II atM0= 0. 5 , while the large dashes line with dot represent results for the G-N theory of type III atM0= 0. 5 .

Fig. 7. The change in the volume fraction field φ distribution at H 0 = 10 5 and θ= 0.

Fig. 8. The induced magnetic field h distribution at H 0 = 10 5 and M 0 = 0.

Fig. 9. The strain e distribution at H 0 = 10 5 and M 0 = 0.

Fig. 2 depicts that the distribution of the induced magnetic fieldhdecreases with the increase in value of Thomson parameter in the range 0 ≤y≤ 0.8, then converges to 0.

Fig. 3 expresses that the distribution of the straineincreases with the increase in value of Thomson parameter in the range 0 ≤y≤ 1.5, then converges to 0. Fig. 4 shows that the Thomson parameter has a decreasing effect, where, the value of the temperatureTis decreases when the Thomson parameterM0increases. In Fig. 5 , the effect of parameterM0exists, since, the value of the stress σincreases when the parameterM0increases. Fig. 6 explains that the distribution of the tangential stress component σxydecreases with the increase in value of Thomson parameter in the range 0 ≤y≤ 0.8, then converges to 0. In Fig. 7 , the value of the change in the volume fraction field φincreases when the parameterM0increases. It is explained that all the curves converge to 0, and the Thomson parameterM0has a significant role for the distributions of all physical quantities.

Fig. 10. The temperature T distribution at H 0 = 10 5 and M 0 = 0.

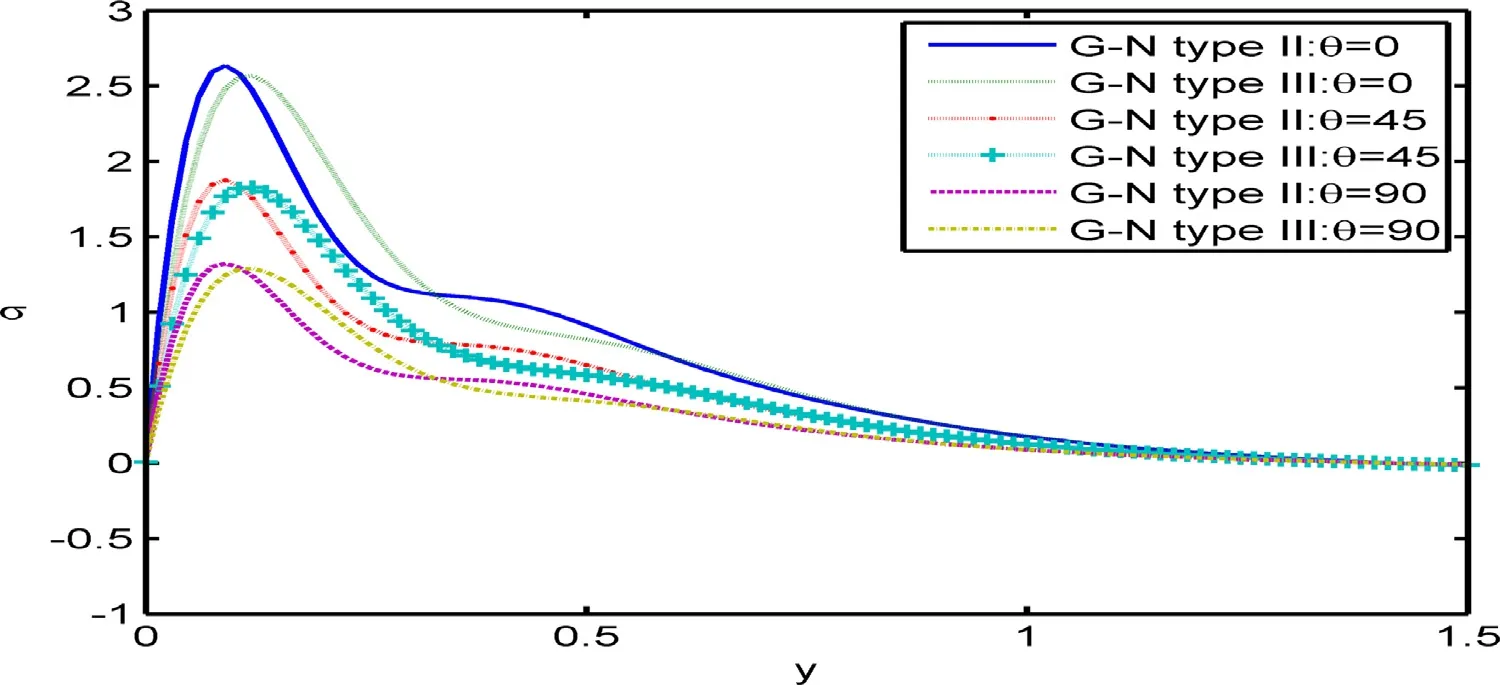
Fig. 11. The stress σ distribution at H 0 = 10 5 and θ= 0.

Fig. 12. The tangential stress σxy distribution at H 0 = 10 5 and θ= 0.

Fig. 13. The change in the volume fraction field φ distribution at H 0 = 10 5 and θ= 0.

Fig. 14. 3D Curve distribution of the induced magnetic field h versus the distances at: M 0 = 0and θ= 0.

Fig. 15. 3D Curve distribution of the tangential stress σxy versus the distances at: M 0 = 0and θ= 0.

Case 2: Figs. 8 –13 give a comparison of the results obtained for the induced magnetic fieldh, the straine, the temperatureT, the stresses σ , σxyand the change in the volume fraction field φagainst theydirection for different values of the angle of inclination θ(θ= 0°, 45°, 90°) atM0= 0. We can note that the angle of inclination θhas significant effects on all the studied fields. Fig. 8 shows that the distribution of the induced magnetic fieldhdecreases with the increase in value of θin the range 0 ≤y≤ 0.7, then converges to 0.Fig. 9 explains that the distribution of the strainedecreases with the increase in value of θin the range 0 ≤y≤ 1, then converges to0. Fig. 10 shows that the angle of inclination θ has large effects on the value of the temperatureTwhich means thatTdecreases with θFig. 11 depicts that the distribution of the normal stress σdecreases when the value of θ in the range 0 ≤y≤ 1.2, then converges to 0. Fig. 12 explains that the distribution of the tangential stress component σxyincreases with the increase in value of θin the range 0 ≤y≤ 1,then converges to 0. In Fig. 13 , the value of the change in the volume fraction field φ decreases when the value of θ increases.

Figs. 14 and 15 are giving 3D surface curves for the physical quantities i.e., the induced magnetic fieldhand the tangential stress field σxyfor generalized electro-magnetothermoelasticity with voids under Thomson effect and inclined loud effect. These figures are very important to study the dependence of these physical quantities on the vertical component of distance.

6.Conclusions

Analysis of induced magnetic field, the strain, temperature distribution, normal stress, tangential shear stress and change in the volume fraction field due to mechanical load and Thomson effect in a semi-infinite generalized electromagneto-thermoelastic medium with voids is an interesting problem of mechanics. The generalized theory of thermoelasticity in the context Green–Naghdi of type II and III is used to solve this problem. A normal mode technique has been used which is applicable to a wide range of problems of thermoelasticity. This method gives exact solutions without any assumed restrictions on the actual physical quantities that appear in the governing equations of the problem considered.The effects of the Thomson parameter and angle of inclination on the field variables are investigated. The results concluded from the above analysis can be summarized as follows:

•The field equations of the theory of homogeneous and isotropic generalized electro-magneto-thermoelasticity with voids under Thomson effect and angle of inclination effect are derived.

•Analytical solutions based upon normal mode analysis for thermoelastic problem in solids have been developed and utilized.

•The effect of Thomson parameter on all the studied fields is very much significant.

•Significant difference in values of the studied fields is noticed for different values of the angle of inclination.

•The deformation of a body depends on the nature of the applied forces and Thomson effect as well as the type of boundary conditions.

•The value of all physical quantities converges to zero with increase in distanceyand all functions are continuous.