Oblique closed form solutions of some important fractional evolution equations via the modified Kudryashov method arising in physical problems
F. Ferdous , M.G. Hafez
Department of Mathematics, Chittagong University of Engineering and Technology, Chittagong, 4349, Bangladesh
Abstract The paper deals with the obliquely propagating wave solutions of fractional nonlinear evolution equations (NLEEs) arising in science and engineering. The conformable time fractional (2 + 1)-dimensional extended Zakharov-Kuzetsov equation (EZKE), coupled space-time fractional (2 + 1)-dimensional dispersive long wave equation (DLWE) and space-time fractional (2 + 1)-dimensional Ablowitz-Kaup-Newell-Segur (AKNS) equation are considered to investigate such physical phenomena. The modified Kudryashov method along with the properties of conformable and modified Riemann-Liouville derivatives is employed to construct the oblique wave solutions of the considered equations.The obtained results may be useful for better understanding the nature of internal oblique propagating wave dynamics in ocean engineering.
Keywords: Fractional nonlinear evolution equations; Conformable derivative; Modified kudryashov method; Oblique wave solutions.
1.Introduction
It is well established that solitary waves on water has been an interesting topic. For instance, the model may be used to understand the run-up of ocean waves such as tsunami waves on dykes and dams [1] . Zabusky and Kruskal [2] have provided the idea of a soliton for the Korteweg-de Vries (KdV)equation arising in water wave dynamics. Zhang and Yishen Li [3] have reported the bidirectional solitons on water. Subsequently, many researchers [4–10] have derived various types of nonlinear evolution equations (NLEEs) form model equations for better understanding the nature of wave dynamics in different environments. One can be studied the solitary waves not only on water but also on plasmas, optical fibers,etc. by evaluating the analytical solutions of NLEEs through the mathematical techniques [11–31] , such as the classical Kudryashov method [17] , the ansatz method [18] , improved tan ( φ ( η)/2)-expansion method [19] , the unified method[24–26] and its generalized form [27–29] , modified Kudryashov method [14,16,30,31] and so on. However, most of real world physical scenarios become non-conservative. In such situations, fractional NLEEs are considered for understanding the physical issues arising in water wave theory,fluid dynamics, plasma physics, optical fiber, quantum field theory and so on. There are still several types of physical issues challenges stay to determine analytical solutions of fractional NLEEs. In most of the studies, researcher scholars[11–31] have only focused the wave solutions to the fractional NLEEs by ignoring obliqueness. Hosseini and Ansari[14] have reported the analytical solutions of nonlinear conformable time-fractional Boussinesq equations using the modified Kudryashov method (MKM). Rezazadeh et al. [16] have reported that fractional temporal evolution of optical solitons with quadratic–cubic nonlinearity that comes with a few perturbation terms via MKM. They have mentioned that the re-sults are applicable to mitigate Internet bottleneck that is a growing problem in telecommunications industry.
It is well known that the wave may be inclined to the flow direction by depending on the shape of the object and the speed of the flow. One can be considered oblique wave propagation in any varied instances when a wave is inclined to the flow direction. For instance, a real sea state is more realistically described by composing of a large number of components of differing periods, heights and directions (known as the directional spectrum). In such situations,the directional spectrum should be taken into account for determining an inshore sea state. Very recently, Ferdous et al.[32] have reported the oblique propagating wave solutions of a NLEE via the generalized exp(- φ ( ξ))-expansion method due to the importance of oblique wave solutions in physical instances. However, no work has been reported the oblique propagating wave solutions of fractional NLEEs via modified Kudryashov method (MKM) for better understanding the internal wave generations in science and engineering, especially in ocean engineering. Hence, this work is carried out to evaluate the obliquely propagating wave solutions of some fractional NLEEs, such as the conformable time fractional (2 + 1)-dimensional extended Zakharov-Kuzetsov equation (EZKE)[32,33] , coupled space-time fractional (2 + 1)-dimensional dispersive long wave equation (DLWE) [34–36] , and Spacetime fractional (2 + 1)-dimensional Ablowitz-Kaup-Newell-Segur (AKNS) equation [37] using MKM. Thus, the paper is organized as follows: In Section 2 , the MKM is described for investigating the oblique traveling wave solutions of fractional NLEEs. In Section 3 , the MKM is employed to construct the exact solutions of conformable time fractional EZKE , Spacetime fractional (2 + 1)-dimensional AKNS equation and coupled space-time fractional (2 + 1)-dimensional DLWE with graphical representation. Finally, the conclusions are drawn in Section 4 .
2.Description of MKM
The following fractional NLEEs are considered to describe the modified Kudryashov method (MKM):

where Fis a polynomial ofV(x,y,t) with various fractional partial derivatives and λis a fractional parameter. Eq. (1) can be easily converted to following nonlinear ordinary differential equation (ODE) of integer order by considering the following transformationsV(x,y,t) =U(ξ) with

wherecis a constant and taking the properties of confirmable[38,39] or of modified Riemann-Liouville [40,41] derivates into account:
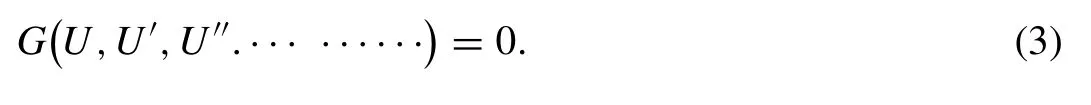
where prime denotes the derivatives with respect to introducing variable ξ. Now, the MKM allows us to write the analytical solution of Eq. (3) as

whereaj(j= 0, 1 , 2, ······,N) are constants which will be calculated later andY( ξ) satisfies the following subsidiary equation:

It is noted that Eq. (5) yields the solution

wheredis an arbitrary constant. The other parameterNas considered in Eq. (4) can be determined by employing homogeneous balance technique in Eq. (2) . Using Eq. (4) in Eq. (3) with the help of Eq. (5) , one can be derived a system of algebraic equations by equating like power ofY( ξ). Simplifying the resulting algebraic equations, the values ofajandcare obtained in terms of the physical parameters. Hence, one can be determined the oblique analytical solutions of fractional NLEEs by combining Eqs. (2) , (4) and (6) . It is to be noted that the MKM is in good agreement with some existing methods [17,24–29] for onlya=e. Otherwise, it will be provided a new type of oblique wave solution to NLEEs.
3.Oblique wave solutions of fractional NLEEs via MKM
This section shows the effectiveness of MKM for demonstrating obliquely propagating wave solutions of some fractional model equations.
3.1. Conformable time fractional (2 + 1)-dimensional EZKE
The following conformable time fractional (2 + 1)-dimensional EZKE are considered for investigating the obliquely propagating internal wave generations not only in water but also in plasmas:

where ρ,σ and μ are all constants. Eq. (7) is an important one for studying numerous physical issues of nonlinear waves in shallow as well as stratified internal waves on water, in plasmas and so on [42,43] .
By use of the variable transform

where cos2θ+ sin2θ= 1 and the properties of conformable time fractional derivates, Eq. (8) can be converted to
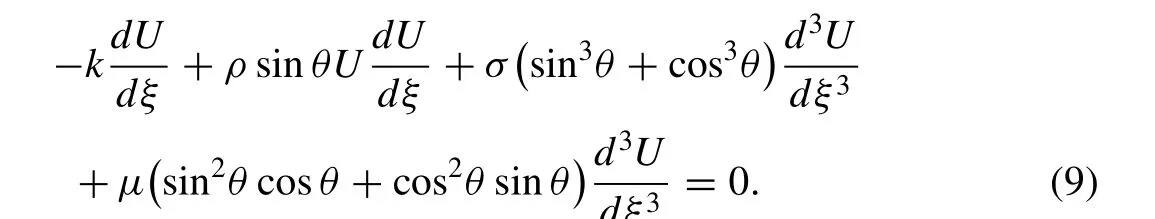
Integrating Eq. (9) with regards to ξ, considering the localized perturbation conditions into account, yields

The solutions of Eq. (10) via the MKM can be written as

Substituting Eq. (11) together with Eq. (5) into Eq. (10) ,the following nonlinear algebraic equations are obtained:

Simplifying the above algebraic equations with aid of manipulation computational software, the values ofa0,a1,a2andkare defined as
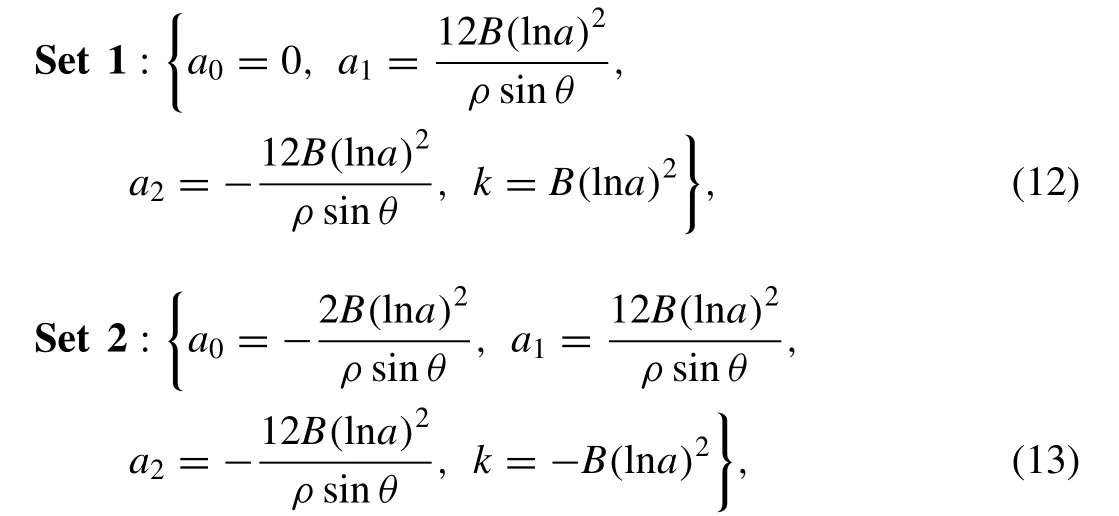
whereB= ( cos θ+ sin θ)[ σ + ( μ − σ ) cos θsin θ] .
Now, combining Eqs. (6) , (8) , (11) , (12) and (13) , the oblique propagating wave solutions of time fractional (2 + 1)-dimensional EZKE are defined as follows:

Wherek=B( lna)2andB= ( cos θ+ sin θ)[ σ + ( μ − σ )cos θsin θ] .
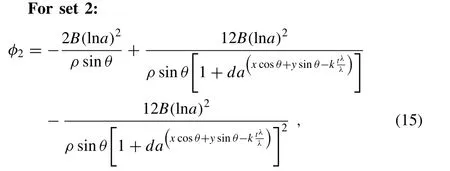
wherek= −B( lna)2andB= ( cos θ+ sin θ)[ σ + ( μ − σ )cos θsin θ] .
The obtained oblique exact solutions of conformable time fractional (2 + 1)-dimensional EZKE are demonstrated by Figs. (1) and (2) , respectively taking the constant values of parameters. It is found the amplitude of the rarefactive wave are decreasing, but smoothly increasing with the increase of obliqueness and fractionality, respectively.
3.2. Space-time fractional (2 + 1)-dimensional ablowitz-kaup-newell-segur (AKNS) equation
The space-time fractional (2 + 1)-dimensional Ablowitz-Kaup-Newell-Segur (AKNS) water wave equation for nonconservative system with a perturbation parameter δcan be written as

By considering the traveling variable wave transform
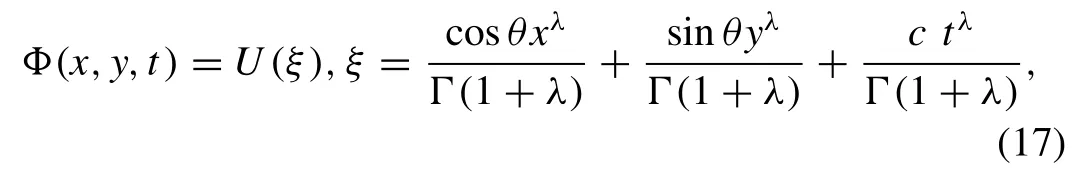
where cos2θ+ sin2θ= 1 and the properties of modified Riemann-Liouville derivates, Eq. (16) is reduced to

Integrating Eq. (18) with regards to ξtaking the localized perturbation conditions into account, one obtains

By employing the MKM, the solutions of Eq. (19) can be written as


Fig. 1. Exact solution φ [Eq. (14)] of EZKE ( 7 ) for (a) λ = 0. 5 , ϑ = π/ 2, a = 1 . 5 , ρ = −1 , μ = 0. 01 and σ = 0. 001 , (b) different values of a with λ = 0. 5 ,ϑ = π/ 2, ρ = −1 , μ = 0. 01 , σ = 0. 001 and t = 1 , (c) different values of λ with ϑ = π/ 3 , a = 2, ρ = −1 , μ = 0. 01 and σ = 0. 001 ,and (d) different values of obliqueness with λ = 0. 5 , a = 1 . 5 , ρ = −1 , μ = 0. 01 and σ = 0. 001 .
Now, substituting Eq. (20) along with Eq. (5) into Eq. (19) ,one can be evaluated the following nonlinear algebraic equations:
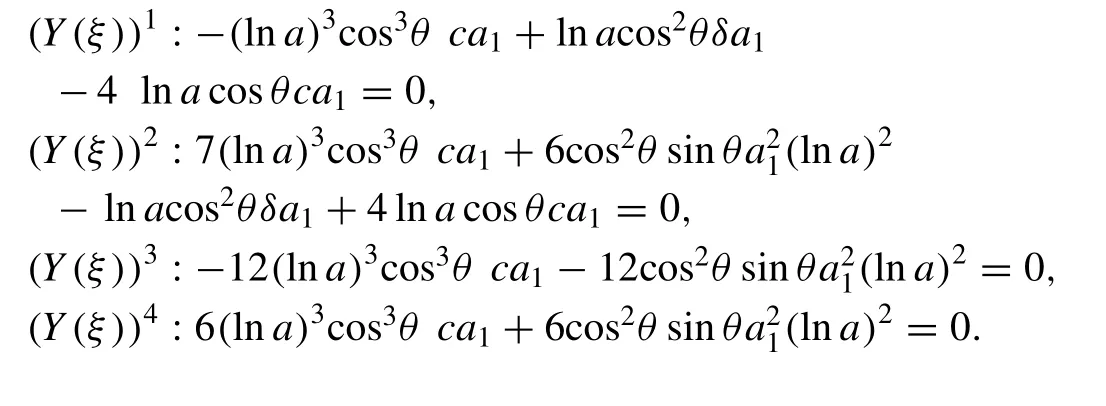
Solving the above algebraic equations, one can be obtained the following values of the considered parameters:
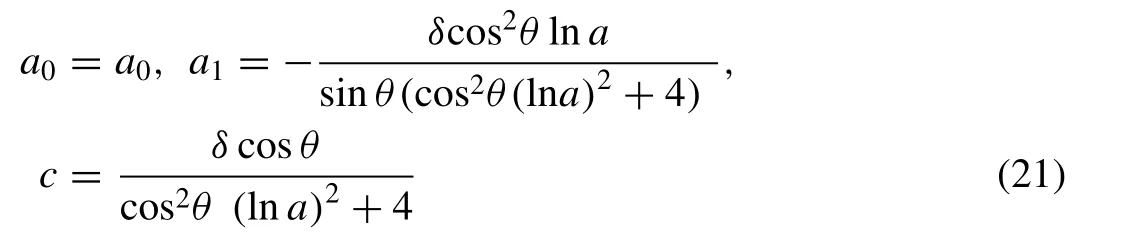
The following oblique propagating wave solution of Eq. (16) is obtained taking Eqs. (20) , (21) and (5) into account:

Fig. 2. Exact oblique solution φ [Eq. (15)] of EZKE ( 7 ) for (a) λ = 0. 5 , ϑ = π/ 2, a = 1 . 5 , ρ = −1 , μ = 0. 01 and σ = 0. 001 , and (b) different values of a with λ = 0. 5 , ϑ = π/ 2, ρ = −1 , μ = 0. 01 , σ = 0. 001 and t = 1 .

The influences of fractional parameter and obliqueness on the exact solution ( 22 ) are provided in Figs. 3 (a) and(b), respectively taking the remaining parameters constant.On the other hand, the obtained exact oblique solution Φ[Eq. (22)] of AKNS water wave Eq. (16) for λ= 0. 5 ,a= 1 . 5 ,ϑ = π/ 4, δ= 0. 01 ,a0= 0. 5 ,d= 0. 5 andt= 5 , and different values ofawith λ = 0. 5 , ϑ = π/ 4, δ= 0. 01 ,a0= 0. 5 ,d= 0. 5 andt= 5 are displayed in Figs. 4 (a) and (b), respectively. Further, the exact oblique solution Φ[Eq. (22)] of Eq. (16) for same typical values of Fig. 4 (a) and different values ofawith the same typical values of Fig. 4 (b) are displayed in Figs. 4 (c) and (d), respectively, except λ= 1 .
3.3. Space-time fractional coupled (2 + 1)-dimensional DLWE
It is found that Benney [44] was first reported that the resonance interactions of long-wave with short-wave for capillarygravity waves in deep water. In such situations, simple interaction equations may not be obtained due to deep water waves,where there is no wave in the long wavelength limit. But,simple interaction equations may be produced in a stable stratified for oblique propagation of long and short-waves [45] .There exist many nonlinear wave equations for describing internal bidirectional resonance phenomena in shallow water, in fluid mechanics etc. In this article, the following space-time fractional coupled (2 + 1)-dimensional DLWE are considered to evaluate internal oblique closed form solutions for understanding long wave interactions propagating toward each other in water wave dynamics:

Here φ1= φ1(x,y,t) indicates the horizontal velocity of water and φ2= φ2(x,y,t) indicates the deviation height from the equilibrium position of the liquid. It is mentioned that Eq. (23) is converted to space-time fractional variant Boussinesq equation takingy=xand φ2= φ1− 1 . In addition,Eq. (23) can be converted to couple dispersive long wave equation with integer order by inserting λ= 1 . Now, let us introduce the following traveling wave transform:

Eq. (23) can be converted, taking the properties of modified Riemann-Liouville derivates into account, to

Fig. 3. Effect of (a) λ with ϑ = π/ 4and (b) ϑ with λ = 0. 5 on the exact solution Φ [Eq. (21)] of AKNS water wave Eq. (16) . The remaining parameters are considered as a = 1 . 5 , δ= 0. 01 , a 0 = 0. 5 , d = 0. 5 , y = 1 and t = 5 .

According to the MKM, the analytical solutions of Eq. (24) can be written as

Inserting Eq. (25) along with Eq. (5) into Eq. (24) , one can be determined the following nonlinear algebraic equations taking the coefficients of ( Y( ξ) )jj= 0, 1 , 2 . . . ) are equal to zero into account:
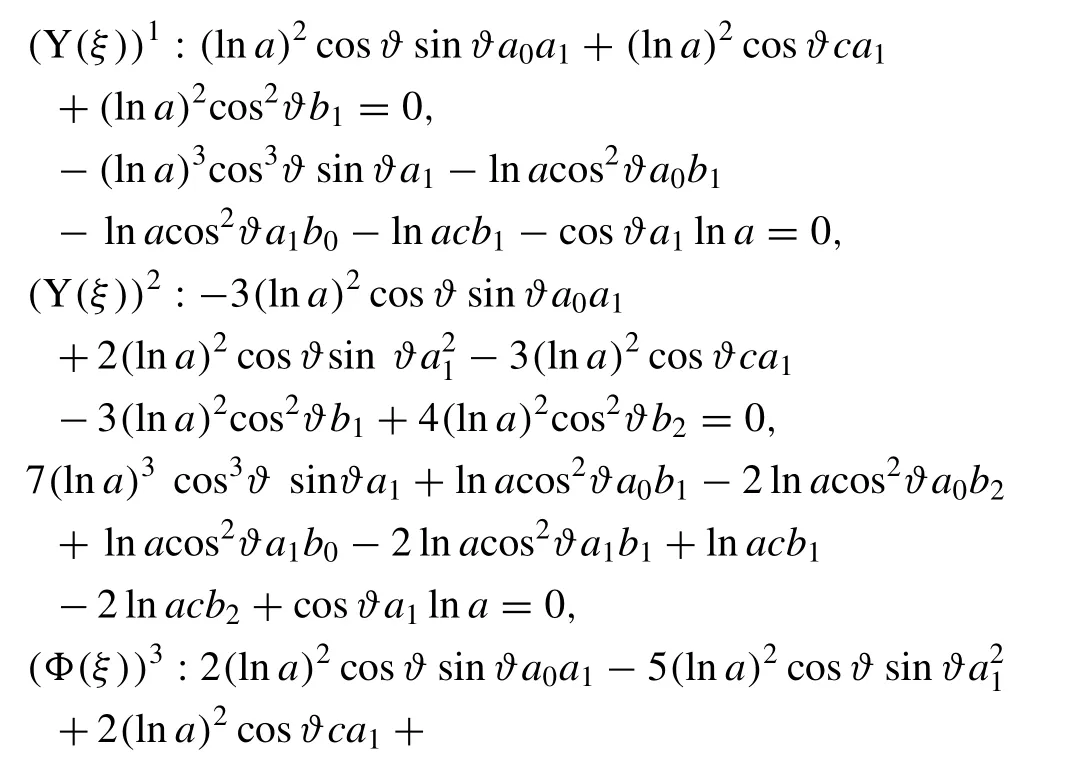
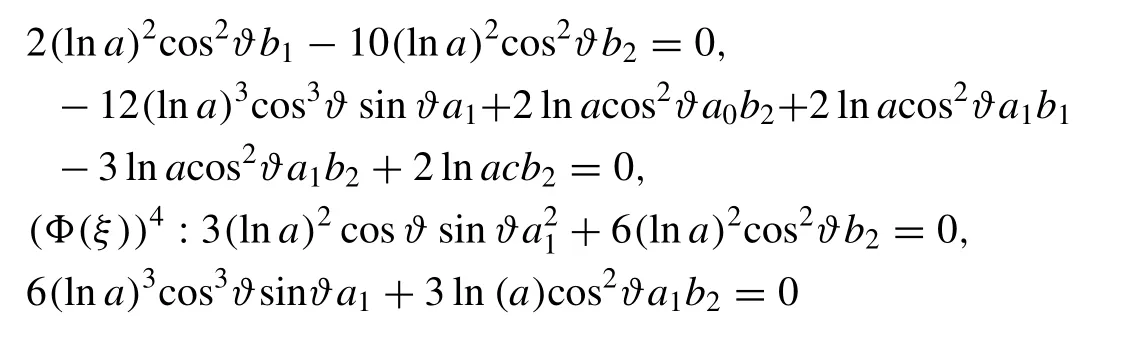
Simplifying the above algebraic equations with the aid of maple software, one can be evaluated the following values for


Fig. 4. Exact oblique solution Φ [Eq. (21)] of AKNS water wave Eq. (16) for (a) λ = 0. 5 , a = 1 . 5 , ϑ = π/ 4, δ= 0. 01 , a 0 = 0. 5 , d = 0. 5 and t = 5 , and(b) different values of a with the same typical values of (a). Exact oblique solution Φ[Eq. (22)] of AKNS water wave Eq. (16) for (c) same typical values of (a), and (d) different values of a with the same typical values of (b).
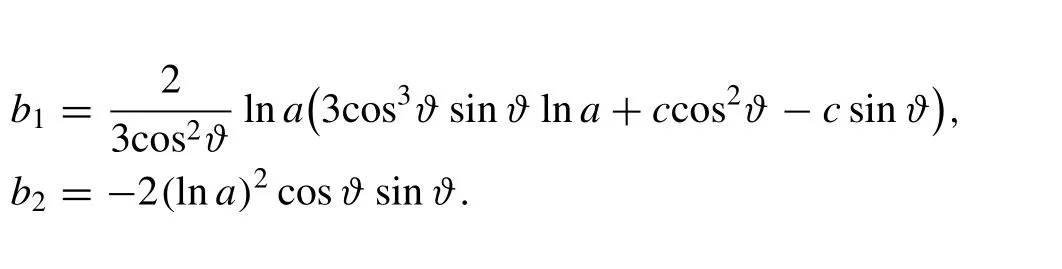
By combining Eqs. (24) , (25) and (6) along with the values ofa0,a1,b0,b1andb2, the following solutions, describing the oppositely propagating internal long waves, of space-time fractional (2 + 1)-dimensional DLWE are obtained:
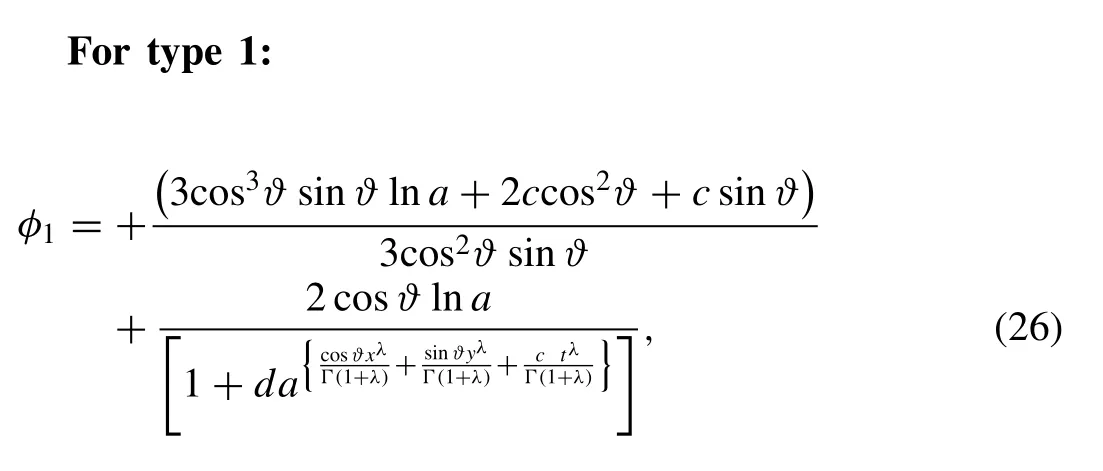

Fig. 5. Oblique interacting wave solutions of DLWE ( 23 ) taking φ1 [Eq. (26)] and φ2 [Eq. (27)] into account for (a) λ = 1 and λ = 0. 5 . The remaining parameters are considered as ϑ = π/ 4, t = 1 , a = 3 and c = 1 .


The oblique interacting wave solutions of Eq. (23) taking φ1[Eq. (26)] and φ2[Eq. (27)] into account for (a) λ = 1 and (b) λ= 0. 5 is displayed in Fig. 5 with constant values of ϑ = π/ 4,t= 1 ,a= 3 andc= 1 .
4.Conclusions
The conformable time fractional (2 + 1)-dimensional EZKE, coupled DLWE and AKNS equation have assumed for reporting higher order oblique propagating wave solutions in any varied instances. The MKM has been employed to obtain oblique exact solutions of the considered equations. It is found that the obliqueness and fractionality are significantly modified the nature of oblique propagating wave dynamics. The obtained results would be helpful in understanding the nature of internal oblique propagating wave dynamics not only in ocean engineering but also in any varied instances.
 Journal of Ocean Engineering and Science2018年3期
Journal of Ocean Engineering and Science2018年3期
- Journal of Ocean Engineering and Science的其它文章
- An integral panel method for the hydrodynamic analysis of hybrid contra-rotating shaft pod propulsors
- RANSE-based simulation and analysis of scale effects on open-water performance of the PPTC-II benchmark propeller
- Efficient three-dimensional high-resolution simulations of flow fields around cylinders
- On application of three-dimensional linearized potential-flow model for shallow-water planing
- Development and validation of a coastal ocean forecasting system for Puerto Rico and the U.S. virgin islands
- Numerical study of self-adjoint singularly perturbed two-point boundary value problems using collocation method with error estimation
