基于GPU加速策略的稀疏反演表面多次波压制方法

张文武， 刘玉敏， 杨建华， 张晟瑞， 王 程， 白玉胜， 石 颖

( 1. 东北石油大学 地球科学学院，黑龙江 大庆 163318； 2. 东北石油大学 电气信息工程学院，黑龙江 大庆 163318； 3. 大庆钻探工程公司 地球物理勘探一公司，黑龙江 大庆 163357； 4. 中国石油集团测井有限公司 生产测井中心，陕西 西安 710201 )

0 引言

常规的表面多次波压制方法有两种[1]：滤波法和基于波动方程的预测相减法。滤波法利用一次波与多次波的可分离性压制多次波[2-6]，对于复杂构造的地震数据，一次波和多次波的可分离性低，不能有效保护有效信号。基于波动方程的预测相减法以地震物理学为基础，包含多次波预测和自适应相减两部分，能够适应复杂地质构造[7-9]，但是自适应相减部分存在伤害有效信号的风险[10-13]。

稀疏反演法建立在与反馈迭代法相同的理论基础上，通过迭代反演方式估计震源子波和地下一次波脉冲响应，进而重构一次波和多次波[14]，省去自适应相减部分，可以更好地保护有效信号。Vanborselen R G等提出参数反演方法，在震源子波已知和能量最小的约束条件下估计一次波[15]；Biersteker J假设一次波能量最小，利用二维反褶积法估计缺失的浅层有效信号[16]；Amundsen L利用上、下行波场的多维除法估计一次波，虽然不需要已知震源子波信息，但需要直达波信息，特别是近偏移距的直达波信息[17]；Wang Y利用基于显式矩阵的反演方法估计有效波，可以消除由近偏移距缺失导致的压制效果不理想，但包括多次波预测和自适应相减两部分[18]；Berkhout A J在逆数据域估计一次波和多次波，省去自适应相减部分[19]，但大量的矩阵求逆运算存在反演风险[20]；Herrmann F J等在曲波域估计一次波，需要预测的多次波指导分离过程[21]。在SRME(Surface-Related Multiple Elimination)理论基础上，Groenestijn G J A V等提出基于稀疏反演估计一次波的方法(EPSI, Estimation of Primaries by Sparse Inversion)，可以避免对有效波的损伤[14,22]，但高计算成本是制约EPSI方法发展的主要因素。

基于CUDA架构的GPU加速技术在处理矩阵运算方面优势明显，广泛应用于地震数据处理方面[23-25]。为解决EPSI方法大量的矩阵运算，笔者在传统的GPU加速方法的基础上进行改进，实现所有频率成分的同步运算，并减少主机端和设备端的数据传输，相比传统GPU加速的EPSI方法和常规EPSI方法，计算效率更高。

1 EPSI方法原理

根据Rayleigh Ⅱ积分和数据矩阵的概念[9]，接收到的上行总波场的单频表达形式为

P=X0S+X0R-P,

(1)

式中：P为接收的上行总波场；X0为一次波脉冲响应；S为震源特性；R-为地表反射系数。对于海洋数据，R-=-1，X0和S的乘积为有效波P0(不在自由表面发生反射的波，包括一次波和层间多次波)。X0、R-和P三者的乘积为自由表面多次波M。不同于SRME方法，EPSI方法不引入自适应算子A，直接把X0和S作为未知量，通过不断迭代反演估计两者的值。尽管假设反射系数R-=-1，但式(1)的未知量(X0和S)多于已知量(P)，为欠定方程，有多解，需增加约束条件：(1)一次波脉冲响应X0在时间域是稀疏的；(2)忽略震源的方向特性。

式(1)可看作一个反演过程，通过依次求取X0和S，使接收的地震记录与估计的地震记录的残差能量最小。目标函数[26]可表示为

(2)

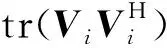
利用最速下降法，经过多次迭代得到X0和S。由于X0和S相互独立，整个过程可分为两部分：(1)固定S，更新X0；(2)固定X0，更新S。EPSI方法的全部过程为

(1)设X0和S的初值为0。

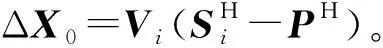
(3)对ΔX0进行稀疏约束：

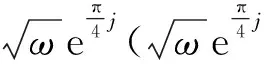
2)变换到时间域，采用合适的时窗(随迭代次数的增加而增大，可以加快收敛速度)，选取每道振幅的最大值。

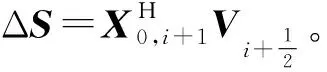
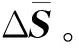
2 基于GPU加速策略的EPSI方法

EPSI方法存在大量矩阵运算，耗费大量时间。GPU加速技术在处理矩阵这类并行度高、密集型强的浮点方面运算优势明显，因此被广泛应用于地震数据处理[23-25]。将GPU加速策略应用于EPSI方法，可

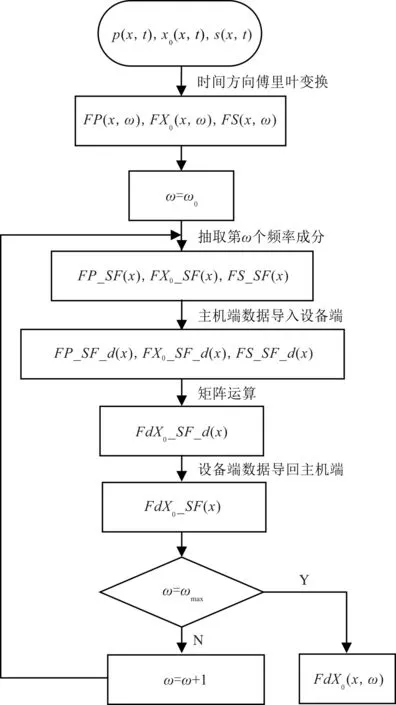
图1 传统GPU加速方法的计算流程Fig.1 Flow chart of traditional acceleration strategy

以提高计算效率，降低计算成本。

CUDA是NVIDIA推出的通用并行计算架构，作为一种运算平台，可以用C语言写出在显示芯片上执行的程序，不需要学习特定的显示芯片指令和特殊结构。GPU加速方法的过程为主机端(CPU及系统的内存)的数据导入设备端(GPU及其显示内存)，在设备端运行核函数[27]，将运行的结果导回主机端。

在传统的GPU加速方法基础上，提出一种新的GPU加速策略。

传统GPU加速方法的计算流程为：(1)将x-t域地震数据在时间方向进行傅里叶变换，得到x-ω域数据。(2)抽取单频成分数据导入设备端。(3)在设备端完成矩阵运算。(4)将运算结果导回到主机端。(5)进行下一频率成分数据的运算，重复步骤(2-4)，直至所有的频率成分计算结束。以求取一次波脉冲响应X0的搜索步长为例，传统GPU加速方法的计算流程见图1。其中，有_SF的表示抽取单频后的数据，有_d的表示设备端的数据，ω0表示选取的初始频率，ωmax表示截止频率。

EPSI方法的不同频率成分之间的矩阵运算相互独立、互不相关，因此在理论上可以同步进行。基于传统GPU加速策略的EPSI方法，没有实现不同频率成分矩阵运算的同步进行，除初始频率成分的计算外，其他频率成分的计算需要等待之前的所有频率成分的计算结束后才能进行，在很大程度上影响算法的计算效率。另外，得到的所有的中间结果需要导回主机端，若它们再次参与计算，仍然需要从主机端导入设备端，中间结果在主机端和设备端之间传导耗费大量的时间。

图2 新的GPU加速策略的计算流程Fig.2 Flow chart of new acceleration strategy

在对传统的GPU加速方法改进后，提出一种新的GPU加速策略，以求取一次波脉冲响应X0的搜索步长为例，计算流程见图2。该策略相比于传统GPU加速方法的优点：(1)所有频率成分整体导入的耗时较抽取单频导入耗时少。(2)可实现多个频率成分运算的同步进行。(3)得到的中间结果除部分必须导回主机端完成运算外，其他的中间结果直接存储于设备端，减少数据在主机端和设备端之间的传导。由于设备端的存储空间有限，当数据体较大、设备端的存储空间不能保存所有中间变量时，需引入多卡GPU的编程策略，处理大的数据体分块，每个卡完成部分数据的运算，减轻单卡的存储负担，提高新的GPU加速策略的适用性[26]。

3 数据测试

3.1 水平层状模型测试

实验模型为单层水平层状介质，正演得到的地震记录有200炮，每炮200道接收，空间方向采样间隔为10.0 m，时间方向1 000个采样点，采样间隔为4 ms，包含两阶多次波。采用EPSI方法，得到不同迭代次数估计的一次波单炮记录(见图3)。由图3可知，随迭代次数增加，一次波同相轴由浅到深被估计出来。抽取该单炮记录的某一道进行对比分析(见图4)，EPSI方法估计的一次波和多次波的曲线与真实的曲线几乎重合。

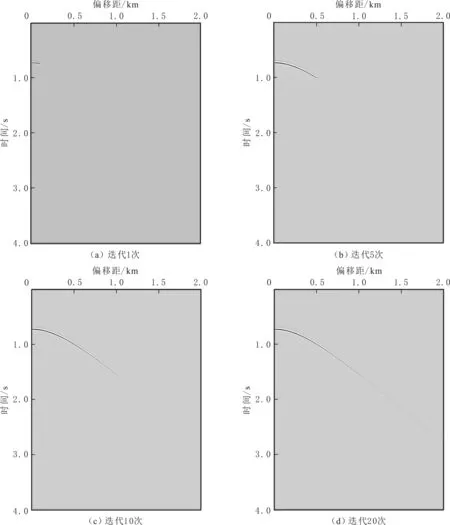
图3 水平层状模型不同迭代次数估计的一次波的单炮记录Fig.3 Single-shot record of estimated primary of horizontal layered by different iterations

3.2 SMAART模型测试

对构造相对复杂的SMAART模型进行测试。地震记录有200炮，每炮200道接收，空间方向采样间隔为22.9 m，时间方向626个采样点，采样间隔为8 ms。采用EPSI方法，得到不同迭代次数的单炮记录(见图5)。由图5可知，随迭代次数增加，一次波的同相轴由浅到深被估计出来，拟合残差逐渐减小。抽取该单炮记录的某一道进行分析(见图6)，EPSI方法估计的一次波和多次波的曲线与真实的曲线几乎重合。

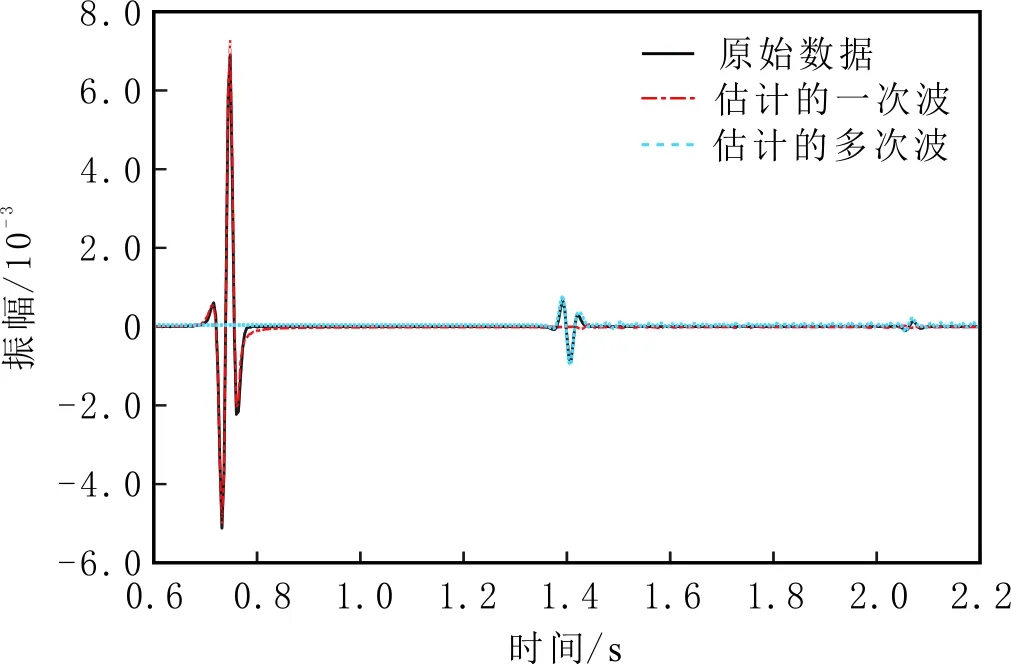
图4 水平层状模型单道记录Fig.4 Single-trace record of horizontal layer model

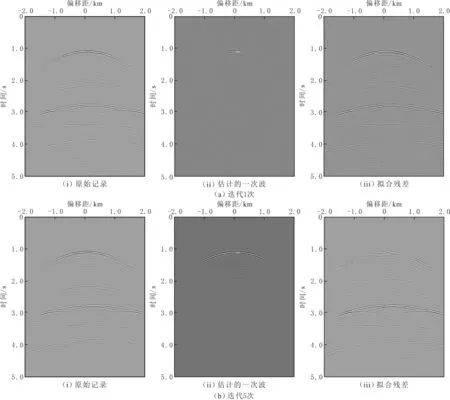
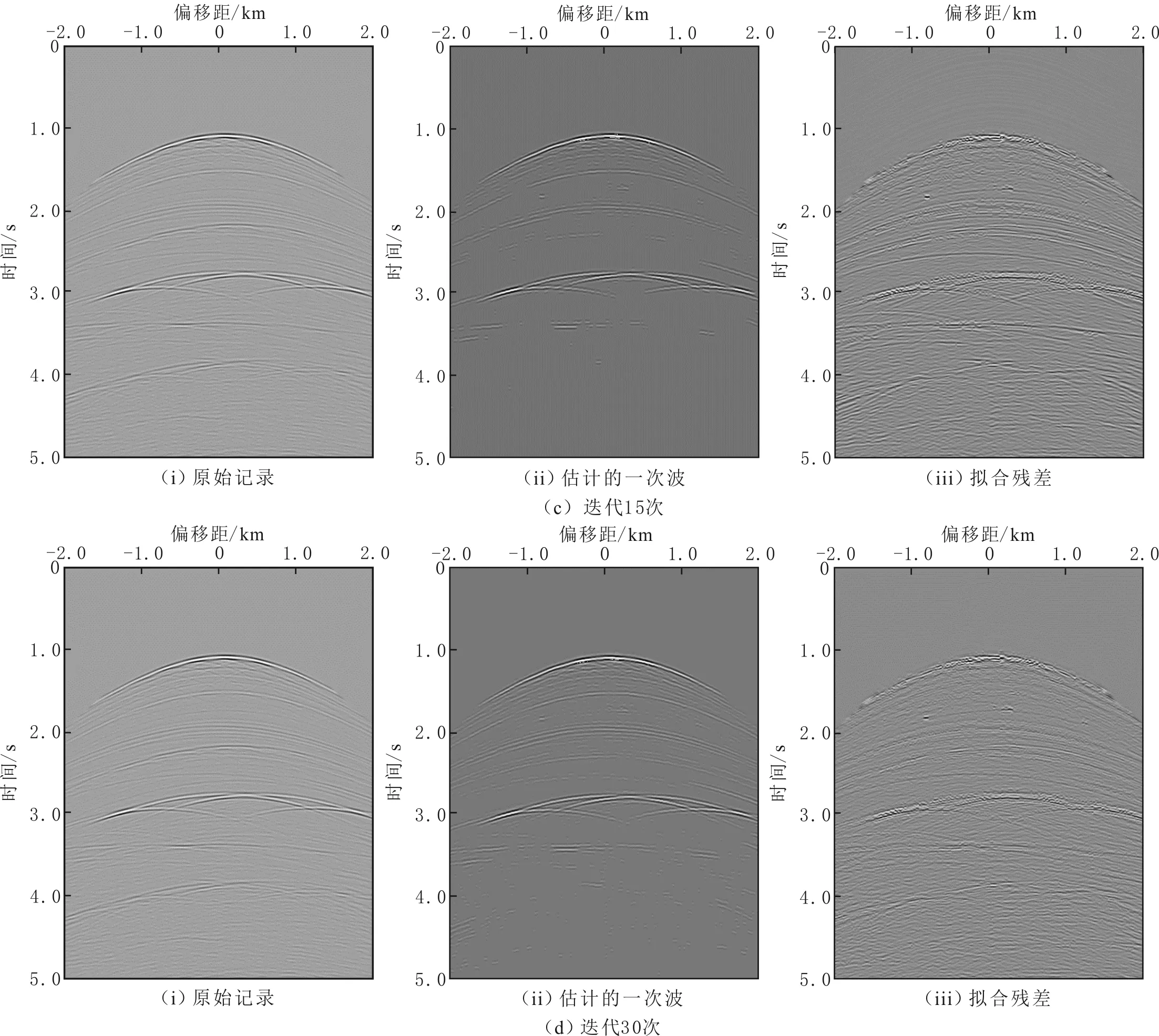
图5 SMAART模型不同迭代次数估计的一次波的单炮记录Fig.5 Single-shot record of SMAART model in different iterations

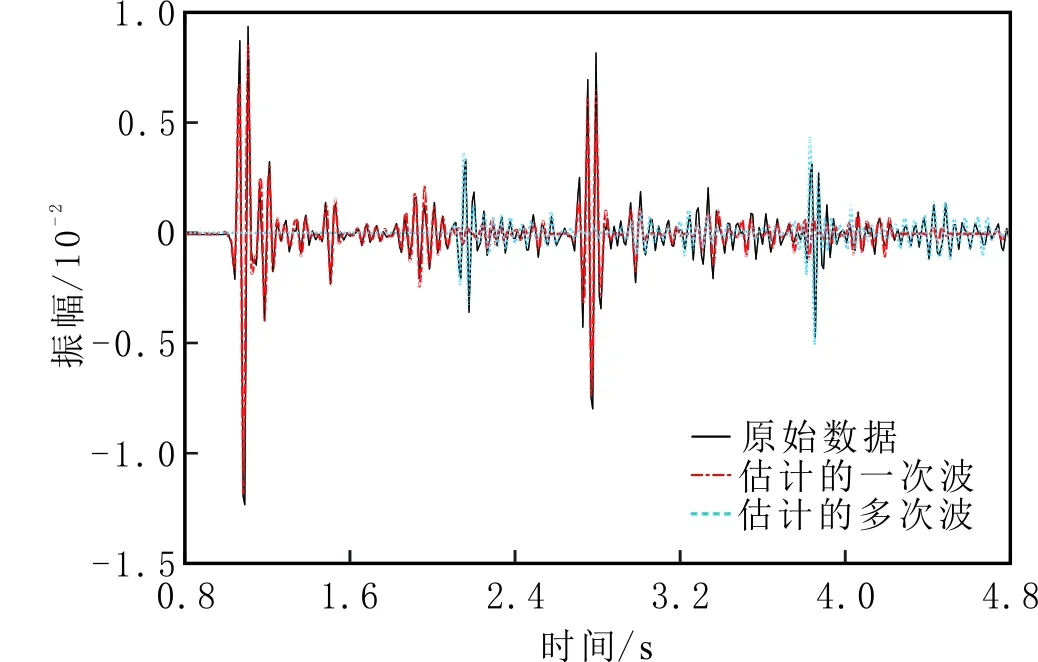
图6 SMAART模型单道记录Fig.6 Single-trace record of SMAART model

EPSI方法压制多次波前后的零偏移剖面的结果见图7，其中箭头标记处表明EPSI方法能够有效的压制多次波。EPSI方法与SRME方法压制多次波后的结果的局部放大(2.2～2.6 s)见图8。由图8可知，采用EPSI方法压制多次波后同相轴更加连续，可以更好地保护有效信号。

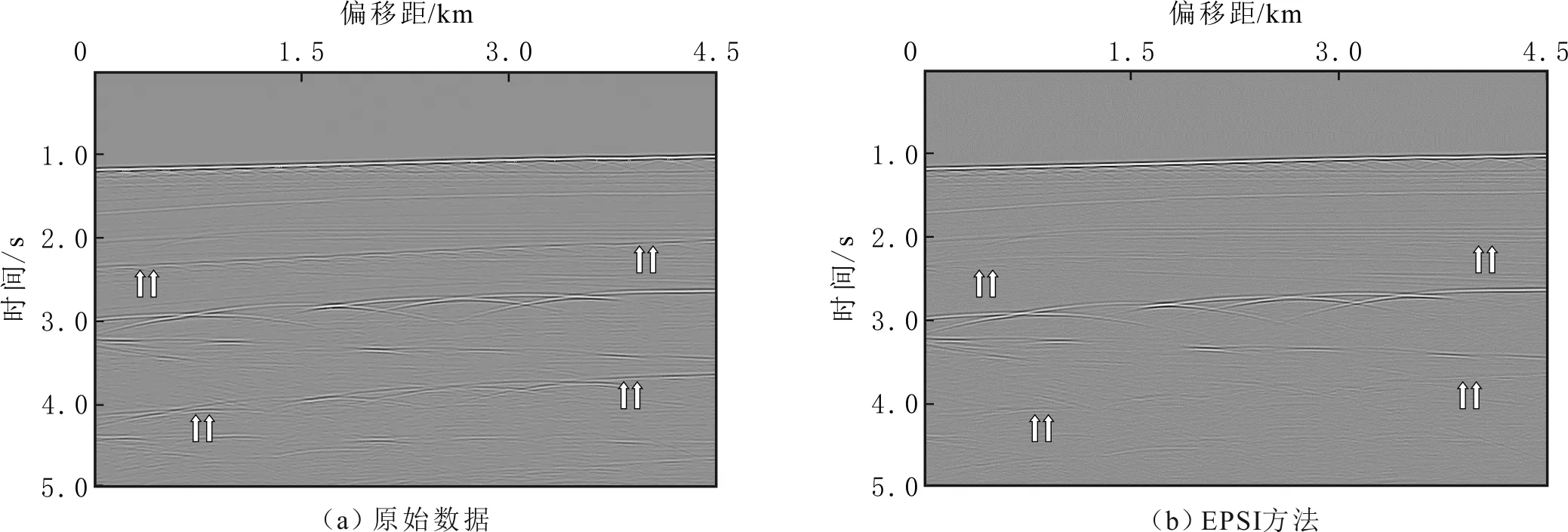
图7 EPSI方法压制多次波前后零偏移距剖面Fig.7 Zero-offset profiles before and after multiple suppression by the EPSI method

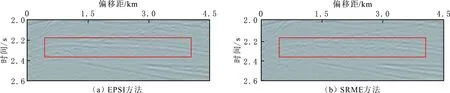
图8 EPSI和SRME方法压制多次波后的零偏移距剖面的局部放大Fig.8 Zoomed-in sections of zero Offset profile after multiple supression by EPSI and SRME methods

3.3 加速比测试

分别用常规EPSI方法、基于传统GPU加速的EPSI方法和基于新GPU加速策略的EPSI方法，处理SMAART模型的地震记录，迭代30次计算耗时见图9。其中：CPU表示常规EPSI方法；GPU_Global表示存储器为全局存储器的、基于传统GPU加速的EPSI方法；GPU_Share表示存储器为共享存储器的、基于传统GPU加速的EPSI方法；GPU_New表示基于新GPU加速策略的EPSI方法。由图9可知，基于新GPU加速策略的EPSI方法的计算效率较常规EPSI方法的计算效率提升11倍，较基于传统GPU加速的EPSI方法提升4倍；不同存储器类型的、基于传统GPU加速的EPSI方法的运行时间几乎相等。通常情况下，存储器为共享存储器的运算速度是存储器为全局存储器的运算速度的2倍，由于数据传输的时间远远大于在设备端计算的时间，因此两种方法总计算耗时相似。

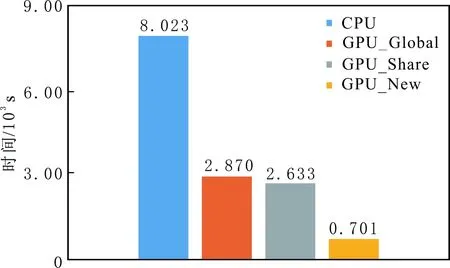
图9 不同方法的计算耗时Fig.9 Time cost of different methods

以SMAART模型为例，根据基于新GPU加速策略的EPSI方法和常规EPSI方法的运行结果，验证前者正确性。两种方法估计的一次波单炮记录见图10。由图10可知，两种方法估计一次波的同相轴形态和位置几乎一致。两种方法估计的一次波频谱见图11。由图11可知，两者频谱曲线几乎重合。两种方法估计的一次波单道见图12。由图12可知，两种方法的单道曲线形态几乎一致，表明新GPU加速策略的EPSI方法正确有效。

图10 两种方法估计的一次波单炮记录Fig.10 Single-shot record of estimated primary by two methods

图11 两种方法估计的一次波频谱Fig.11 Spectrum comparsion of the estimated primary by two methods

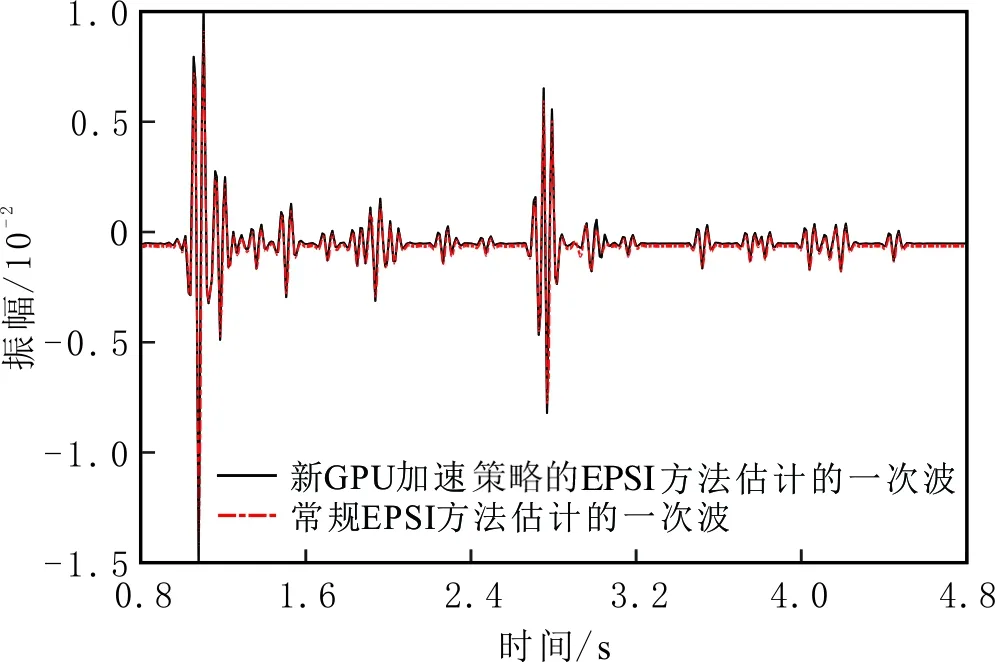
图12 两种方法估计的一次波单道记录Fig.12 Single-trace record of the estimated primary by two methods

4 结论

(1)基于新GPU加速策略的EPSI方法将所有频率成分整体导入设备端，并将中间结果存储于设备端，实现所有频率成分的同步运算，减少主机端和设备端的数据传输时间，相比于传统GPU加速的EPSI方法，计算效率更高。

(2)SMAART模型测试结果表明，基于新GPU加速策略的EPSI方法的计算结果正确有效，可以应用于地震资料的表面多次波的压制。