基于螺旋导引槽空心锭子的喷气涡流纺加捻腔流场模拟

闫琳琳， 邹专勇， 卫 国， 程隆棣

(1. 绍兴文理学院 浙江省清洁染整技术研究重点实验室， 浙江 绍兴 312000； 2. 东华大学 纺织面料技术教育部重点实验室， 上海 201620； 3. 百隆东方股份有限公司， 浙江 宁波 315206)

喷气涡流纺技术作为一种借助高速气流加捻成纱的新型纺纱技术，具有速度高、能耗低、毛羽少等显著优势，发展潜力巨大，但其成纱强力偏低的问题，严重限制了喷气涡流纺技术及其产品的发展[1-2]。加捻腔区域(由纤维导入元件、喷嘴和空心锭子组成)内流场的流动规律对喷气涡流纺的加捻成纱过程具有决定性的影响，但加捻腔区域复杂、结构精细和加工过程的封闭，为实验研究和在线检测加捻腔内流体规律带来了极大的困难。随着基于流体动力学的数值模拟方法在纺织加工领域的广泛应用，为研究喷气涡流纺加捻腔内气流流动规律和深入理解成纱机制提供了有效研究手段[3]。 国内外研究者借助数值计算方法，已掌握喷气涡流纺喷嘴内部的气流流动规律，且对喷气涡流纺的成纱机制、成纱结构和性能有了较为深入的理解[4-6]。也有大量针对喷嘴气压[7-9]、喷嘴结构参数[10-12]等对喷嘴内部气流流动规律影响的研究，进一步讨论了喷嘴内流场变化对喷气涡流纺成纱结构和性能的影响，并探索优化成纱工艺参数的方法[13]。然而，现有研究鲜有从成纱机制分析出发开展喷气涡流纺纱线强力提升的探索，Han等[14]尝试对空心锭子外表面进行刻槽处理，通过增加自由尾端纤维与空心锭子表面的摩擦实现纤维绕纱尾旋转的同时，产生自身的扭转现象，进而提高纤维间的抱合力和成纱强力，但对空心锭子外表面简单的刻槽处理，并不能达到显著提升喷气涡流纺成纱强力的效果。为此，本文提出一种带有螺旋导引槽的空心锭子的设计理念，并利用数值分析方法从理论上研究加捻腔区域和空心锭子外表面螺旋导引槽附近区域的流场特征，以阐明具有螺旋导引槽的空心锭子设计的科学性，并进一步分析其对喷气涡流纺成纱过程与性能的影响规律。

1 加捻腔三维流场区域模拟

1.1 计算流体动力学模型构建

基于螺旋导引槽的空心锭子结构如图1所示。

图中显示从空心锭子入口向下，在其外表面周向设计有螺旋角为θ的导引槽，且要求俯视图中螺旋导引槽的曲率半径rg为常数。螺旋角是指俯视图中，空心锭子中心点与相邻导引槽中心线结束点连线的夹角。本文选择8条螺旋导引槽，导引槽螺旋角为45°，曲率半径rg为2.5 mm，旋转方向与喷孔旋向相同，导引槽深度d(0.08 mm≤d≤0.4 mm)由上向下逐渐加深，导引槽宽度L(0.1 mm≤L≤0.5 mm)从上向下逐渐加宽，由此构建三维流场计算区域，如图2所示。

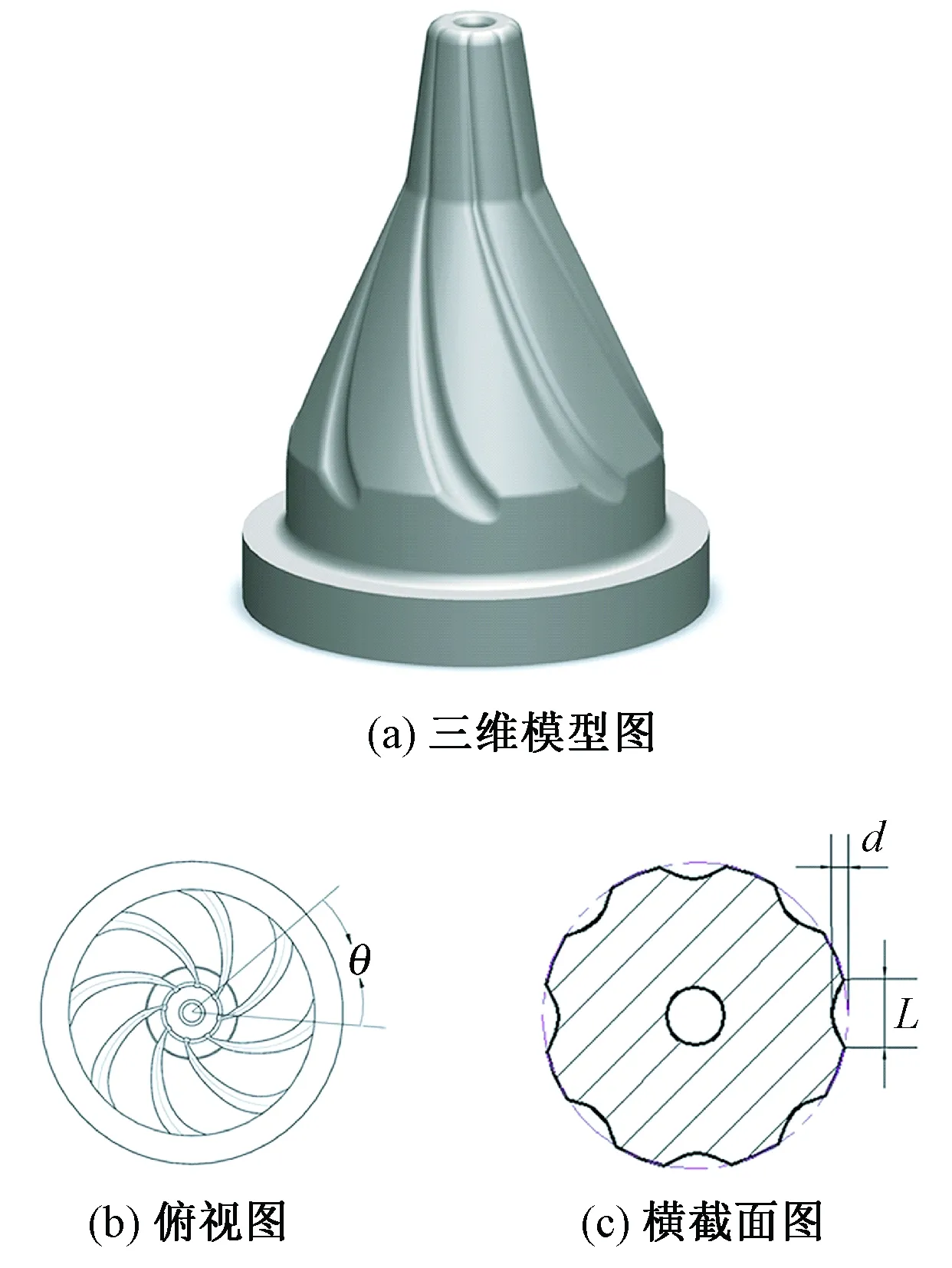
图1 带螺旋导引槽的空心锭子结构Fig.1 Structure of hollow spindle with spiral guiding grooves. (a) Three-dimensional model; (b) Top view; (c) Cross sectional view

图2 纱线加捻成形三维流体动力学计算区域Fig.2 Three dimensional flow field of yarn formation

喷气涡流纺的加捻腔是指喷嘴与空心锭子之间构成的加捻区域，压缩空气经喷孔释放后在此区域形成高速旋转气流，流场视为具有湍流特征的高速、黏性、可压缩流动，在不考虑纤维存在时可视为定常流动，因此，加捻腔流场数值计算采用的质量守恒、动量守恒和能量守恒控制方程分别如下：

(1)

(2)

(3)

式中：ρ为流体密度，kg/m3；t为时间，s；μi为流体沿i方向的速度分量，m/s；p为流体压力，Pa；πij为应力矢量；gi为沿i方向的体力分量，m/s2；Fi为由于阻力和能源而引起的其他能源项，Pa/m；h为焓，J/kg；km为分子传导率, W/(m·K)；kt为由于湍流传递而引起的传导率, W/(m·K)；sh为定义的体积源，W/m3；T为气体热力学温度，K。

为使上述方程封闭，补充如式(4)所示的理想气体状态方程：

p=ρRT

(4)

式中：R为摩尔气体常数，J/(mol·K)。

由于流动处于湍流状态，还需附加湍流输运方程，本文采用realizablek-ε模型，湍动能k(m2/s2)和湍流耗散率ε(%)分别对应的方程为：

Gκ+Gb-ρε-YM+Sκ

(5)

(6)

式中：Gκ为由于平均速度梯度引起k的产生项，无量纲单位；Gb为由于浮力引起的k的产生项，无量纲单位；YM为可压湍流中脉动扩张的贡献，无量纲单位；μ为分子黏性系数，Pa·s；μt为湍流黏性系数，Pa·s；S为广义源项；Sκ、Sε为用户定义的源项；ν为气体运动黏度系数，m2/s；经验常数：C2=1.9，σκ=1.0，σε=1.2，C1ε=1.44[15]。

1.2 计算流体动力学模型数值计算

1.2.1网格划分和边界设定

计算模型采用非结构四面体网格进行划分，为保证网格的高质量，对局部较精细部位进行精细划分，如图3所示。网格节点数为116 132个，网格单元数为584 051个。

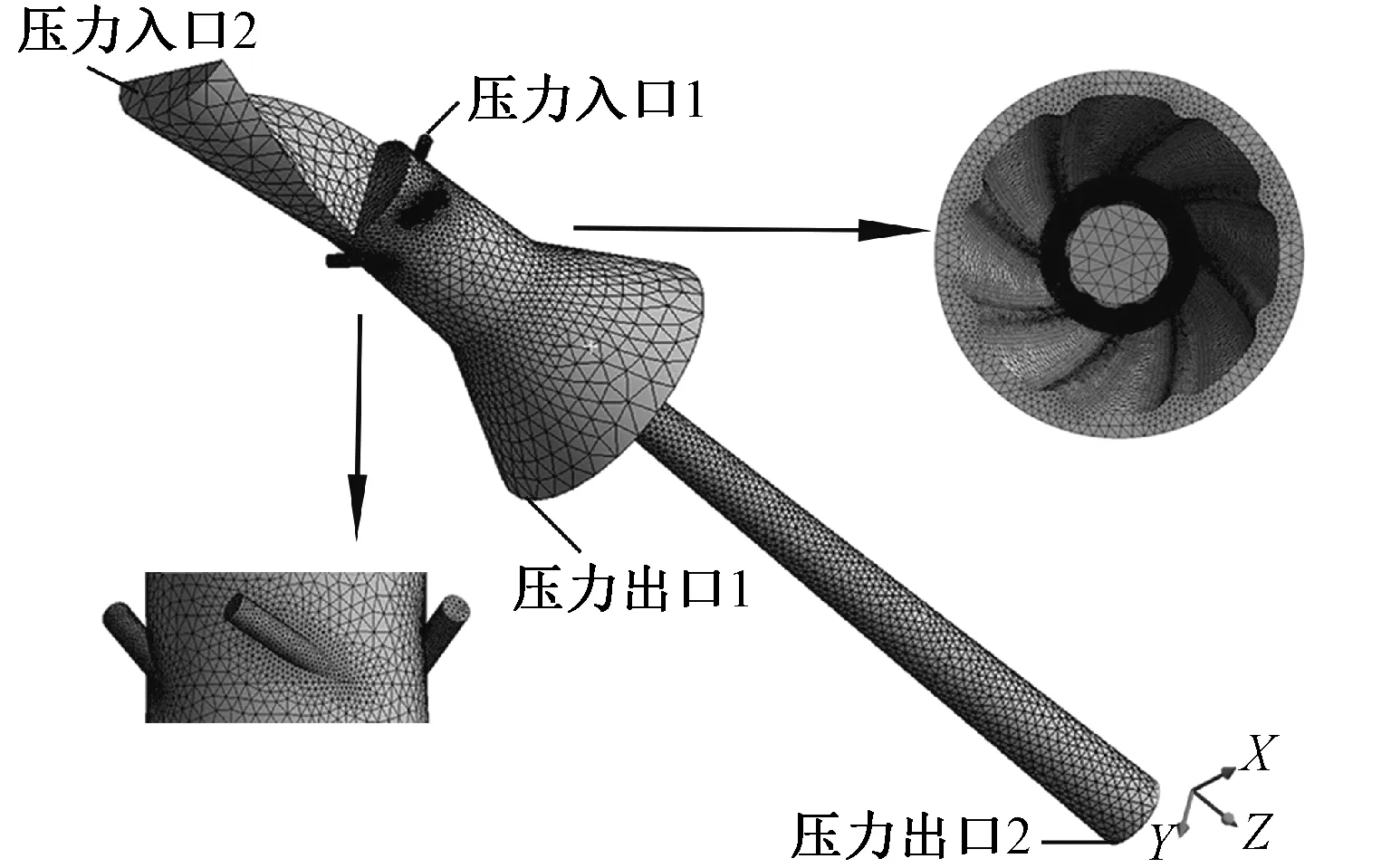
图3 三维计算区域网格划分示意图Fig.3 Grid diagram of 3-D computational domain

数值模拟计算时，4个喷孔进口处设为压力入口1，该处总压设为0.55 MPa，静压由式(7)计算得342 931.5 Pa；螺旋纤维进口处设为压力入口2，该处与大气相通，总压和静压均等于外界大气压。喷嘴内壁和空心锭子外壁形成的气流出口设置为压力出口1，为简化计算该处气压可视为等于外界大气压；导纱通道出口处设为压力出口2，由于与外界相连，该处气压等于外界大气压；其余部分设为无滑移绝热壁面。

(7)

式中：p0为气体总压，Pa；ps为静压，Pa；M为马赫数，取0.85；γ为气体绝热指数，取1.4。

1.2.2求解参数设置

近壁面采用标准壁面函数法，求解控制方程选用压力基耦合求解器，计算通量运用三阶MUSCL离散格式，计算采用并行计算，收敛精度为10-4。

2 结果与分析

2.1 计算流场区域的静压分布

2.1.1静压分布特征

加捻腔流场区域的静压分布如图4所示。其对应的4个代表性横截面位置(Z分别为0.05、1.60、4.47、10.05 mm)处的静压分布及其沿半径的分布规律如图5、6所示。

图4 计算流场区域静压分布Fig.4 Distribution map of static pressure in flow field

由图4、5可看出：喷孔入口处静压值最大，喷嘴入口和空心锭子入口平面之间的中心区域及空心锭子入口平面下部区域存在负压，前者有助于自由尾端纤维顺利吸入喷嘴，后者有助于浮游的纤维从加捻腔顺利排出，防止纤维堵塞加捻腔；由于空心锭子表面螺旋导引槽结构的存在，气流经槽体时会在槽内出现短暂的停滞，而槽体附近的气流由于碰撞到空心锭子外壁，能量损失，静压值减小，使得导引槽内部区域的静压相对导引槽附近区域高，这有利于将进入导引槽的自由尾端纤维更好地带离导引槽。

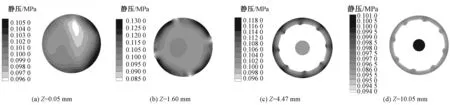
图5 不同Z值下XY截面静压分布Fig.5 Distribution of static pressure in different XY cross sections

图6 不同Z值下XY截面的静压沿半径分布Fig.6 Distribution law of static pressure along radius in different XY sections. (a)At two sections above inlet of hollow spindle; (b) At two sections below inlet of hollow spindle

由图6可看出：加捻腔中各横截面内静压沿半径的分布情况，流场静压整体呈中间低两边高的U形分布。在加捻腔喷嘴入口平面到空心锭子入口平面中心区域的静压值较小，处于负压状态；周边区域的静压值较大，且随着半径的增大静压值增大；这有利于纤维吸入纱尾，同时保证芯纤维的伸直平行。

2.1.2导引槽区域气流静压分布规律

为充分掌握导引槽区域流场的静压分布，选择Z=4.47 mm处XY截面其中1个螺旋导引槽中心线位置对应径向和该区域周向的静压进行分析，如图7所示。

注：A-1、A-2、A-3分别表示空心锭子导引槽内0.05 mm、锭子外表面0 mm和导引槽外0.05 mm圆弧位置。

由图7(a)可知，槽内静压沿着槽深度方向越来越大，且大于空心锭子外壁面处的静压，原因是气流经过槽体时在槽内出现短暂停滞造成，此外导引槽外静压沿着半径方向逐渐增加，这种现象也可从图5得到证实；前者有助于进入导引槽的自由尾端纤维顺利滑出导引槽，后者有助于自由尾端纤维贴服在空心锭子外表面；由图7(b)知，导引槽中心位置较槽两边的静压高，这也有助于自由尾端纤维顺利滑出导引槽。

2.2 计算流场区域的速度分布

2.2.1速度流动特征

加捻腔流场区域的速度矢量图和流线轨迹如图8所示。对应的加捻腔4个横截面位置处速度矢量如图9所示。

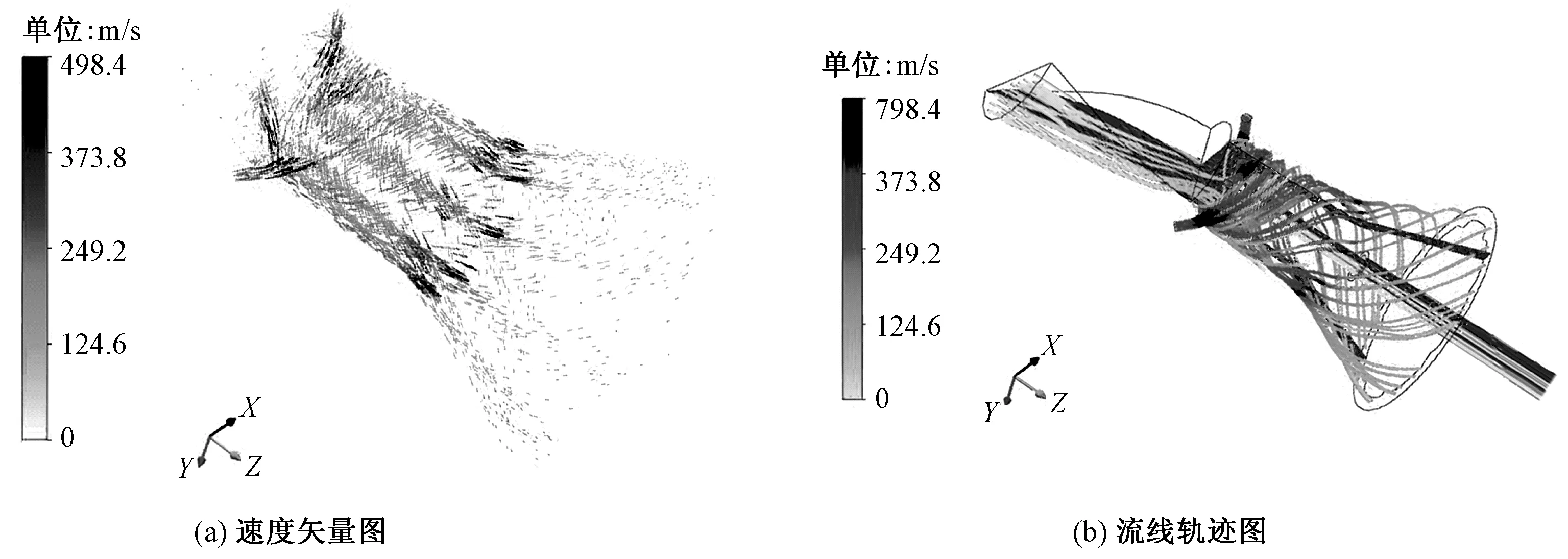
图8 计算流场区域的速度矢量图和流线轨迹图Fig.8 Diagram of velocity vector (a) and streamline (b) of flow field

图9 不同Z值下XY截面速度矢量图Fig.9 Velocity vector chart in different XY cross sections

由图8可看出：压缩空气在喷孔内获得加速，在喷孔出口处达到最大，经喷孔喷出后，进入到加捻腔内形成高速涡流，且气流速度迅速降低；大部分气流经空心锭子与喷嘴之间形成的环形区域排出，少部分从导纱通道排出，且速度很小。此外，空心锭子外表面的螺旋导引槽引导气流向空心锭子与喷嘴之间形成的环形区域流动，这有助于增强加捻腔中的气流流动特征，从而增强自由尾端纤维的加捻效应，最终提升喷气涡流纺的成纱强力。图9很好展示了加捻腔截面内的气流呈高速旋转的涡流状态特征，在喷孔出口处气流速度最大，远离喷孔出口的位置(Z=4.47 mm和Z=10.05 mm)，速度逐渐衰减的现象。

2.2.2加捻腔气流流动沿径向分布规律

根据旋转气流理论，气流场的流动特征决定了气流对纤维的作用力。加捻腔中气流速度可分解为切向、轴向和径向3个方向的速度分量；切向速度决定自由尾端纤维的旋转和加捻效果，促使喷气涡流纱外观形成包缠结构特征；轴向速度使自由尾端纤维倒伏在空心锭子外壁；径向速度有助于对自由尾端纤维束起到膨胀与松懈的作用，从而获得更多数量的包缠纤维。

加捻腔不同Z值时XY截面的气流速度分量沿半径方向的分布规律如图10、11所示。

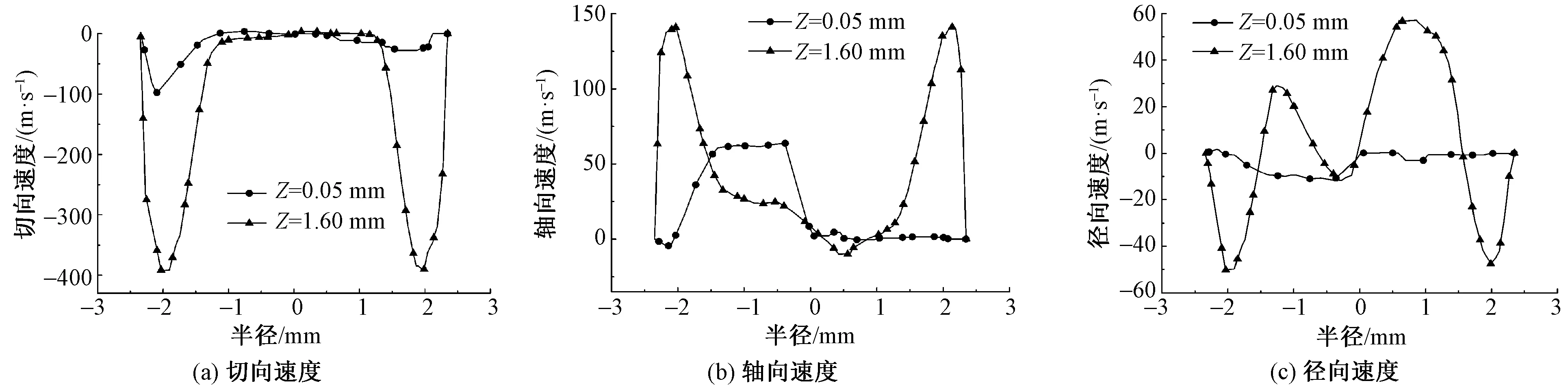
图10 空心锭子入口以上2个XY截面处的速度沿半径分布规律Fig.10 Velocity along radial direction in two XY cross sections above inlet of hollow spindle.

表明越靠近喷孔出口，获得的最大切向速度越大，喷嘴中心位置及近壁区切向速度较小；沿喷嘴半径方向，总体呈现先增加后减小的趋势。较大的切向速度将有助于增强了自由尾端纤维的旋转和加捻，使喷气涡流纱的包缠结构更加紧密；轴向速度和切向速度的变化规律整体相似，但相比切向速度较小，轴向速度易使自由尾端纤维倒伏在空心锭子外表面以更好受切向气流作用而包缠纱尾，但同时对进入纱尾的纤维头端有抽拔作用，是造成落纤与纱线条干恶化的原因之一；径向速度相对较小，且波动较大，尤其是喷孔出口区域，这有利于自由尾端纤维束的膨胀与松懈，促使产生更多的包缠纤维，从而增强纱线的包缠效果，提升纱线成纱强力。

2.2.3导引槽附近区域气流速度分布规律

为掌握导引槽附近区域的气流速度分布，提取Z=4.47 mm处XY截面其中1个螺旋导引槽中心线位置对应径向和该区域周向速度进行分析，结果如图12、13所示。

图12 Z=4.47 mm时XY截面导引槽中心线位置对应径向的速度分布。Fig.12 Velocity along radial direction of guide groove centerline in Z=4.47 mm XY section.

注：A-1、A-2、A-3分别表示空心锭子导引槽内0.05 mm、锭子外表面0 mm和导引槽外0.05 mm圆弧位置。

由图12可知，导引槽中心线对应径向的气流在切向、轴向、径向的速度分量随半径的增加，均呈先上升后下降的趋势；导引槽内部区域的气流速度均小于空心锭子近壁面流场区域的气流速度，这说明进入导引槽内部的纤维运动没有空心锭子外表面的纤维运动剧烈，这导致槽内与槽外纤维的运动速度存在差异，有助于包缠纤维位置的改变，实现纱线截面内纤维的内外转移。此外，由图13可知，导引槽区域周向的气流在切向、轴向、径向的速度分量大小均呈先增大后减小的趋势，导引槽中心线区域拥有较高的气流速度，可由图11得到证实，这有助于自由尾端纤维在气流惯性作用下顺利滑入导引槽，又在导引槽中心较高气流作用下将自由尾端纤维顺利带出导引槽，从而确保自由尾端纤维内外转移的持续性与纺纱的顺利进行，同时自由尾端纤维滑入与滑出导引槽过程中因速度差、摩擦作用等引起纤维绕自身轴线翻转，从而形成自捻效果，最终实现喷气涡流纺纱线强力的提升。而自由尾端纤维的自捻效应对喷气涡流纺纱线强力的增强机制已被文献[16]分析与验证。

3 结 论

对空心锭子进行螺旋导引槽的设计并未改变喷气涡流纺加捻腔旋转涡流的特征，仅影响导引槽附近区域的流场流动。空心锭子外表面的螺旋导引槽的存在可引导气流向空心锭子与喷嘴之间形成的环形区域运动，从而增强加捻腔气流的流动，增强自由尾端纤维的加捻作用，实现纱线强力提高；同时螺旋导引槽内外的气流速度差及摩擦效应会引起自由尾端纤维在纱线截面内产生内外转移与自捻现象，进一步提升喷气涡流纺纱线的强力。此外螺旋导引槽内短暂停滞的较高气压促使进入导引槽的自由纤维顺利滑入与滑出导引槽，确保纺纱的顺利进行。