基于统计和混沌优化BP神经网络融合模型的大坝变形预测分析

陈 婵，田 晔

（江西省安义县水务局，江西 安义330500）

0 引言

大坝原型监测数据的动态变化直接反映其运行性态，基于大坝原型监测数据，构建合理的大坝监测效应量模型并对大坝的监测效应量进行实时预测是大坝安全监控的重要内容，且监测效应量的准确预报对保障大坝的安全运行有着十分重要意义。工程实践表明，大坝监测效应量受到库水压力、温度、坝基、渗流、施工过程、时效等因素的影响，使得坝体、坝基以及近坝库岸构成了一个复杂开放的非线性动力系统[1]。使大坝监测效应量具有混沌动力学特性，其监测的数据序列为混沌时间序列。由于大坝变形监测量直观可靠、精度较高，可通过研究大坝变形的数据序列来反映大坝在环境与荷载互馈作用下变形性态的动态演变。

大坝变形监测的混沌时间序列数据有其特定非线性规律，解析方法一般很难表达这种特性，使得传统统计模型的拟合精度高但预测效果不佳。BP神经网络作为人工神经网络中最重要的网络之一，其特点是具有很强的自适应性和学习模仿能力，在工程中应用极为广泛。大量实践证明，基于误差反传递算法的BP神经网络有很强的映射能力，可有效剖析混沌时间序列的非线性特性。但传统的BP神经网络并未考虑到大坝的混沌动力学特性。因此，本文主要开展以下两方面的研究：①基于统计模型分离出变形监测数据序列中除了可确定成分与随机性成分外，对残差项数据序列进行混沌特性判别；②对于带有混沌特性残差数据序列建立混沌优化BP神经网络模型，从而对大坝变形性态进行预测分析。

1 变形监测数据的混沌特性识别

根据混沌理论，大坝变形监测数据是否具有混沌特性，首先要对数据序列进行相空间重构，然后可从数据的相空间中吸引子是否具有自相似结构的分数维几何体以及数据对于初始状态的条件是否十分敏感两个基本特征判别[2]。前者通常采用关联指数饱和法诊断是否存在分数维；后者采用最大的Lyapunov指数是否大于0进行判断。本文选取最大的Lyapunov指数来确定数据序列的混沌特性。

1.1 重构相空间

在大坝变形数据的时间序列分析中，影响因素复杂众多，其形成的动力学方程是非线性且混沌的。根据Takens定理，通过相空间重构能将混沌时间序列扩展到三维甚至更高维的相空间中，在拓扑变换的意义下恢复原系统的动力学特性，从而可以对系统的发展趋势做出预测[3]。目前，重构相空间通常采用坐标延迟法，把一维变形监测的时间数据序列嵌入到维相空间中[4]：

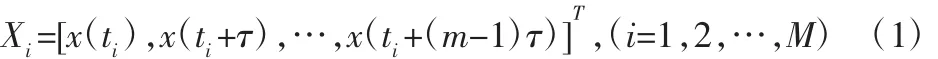
式中：τ=kΔt为时间延迟，k（k=1，2，…，n）为延迟参数，Δt为采样间隔时间；m为嵌入维数；Xi为m维相空间中的相点；M=n-（m-1）τ为相点个数。

由上分析可知，相空间重构质量的好坏取决于重构参数的合理确定，自相关法对延迟时间的确定，以及采用G-P算法确定嵌入维数是讨论的重点。

1.2 嵌入维数的计算

G-P算法最初是由Grassberger和Procaccia提出的，可用于时间序列数据的维数计算[4]。其主要计算步骤为：

1）利用自相关法确定延迟时间τ后，先假定一个值m0（通常比较小），构造一个重构的相空间；

2）通过此重构的相空间计算关联维数C（λ）：

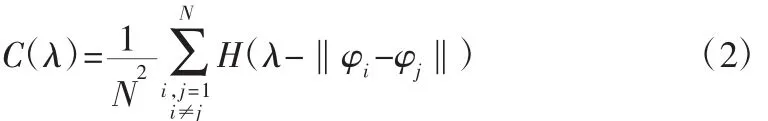
3）当处于某一特定范围时，混沌吸引子的维数与之间有如下对数线性关系：于是可得 m0的维数 d（m0）；

4）重复以上步骤，随着嵌入维数m的增大，在给定误差范围内，d（m）不再随m的增大而发生较大的变化时为止，此时的m即为所求的嵌入维数。

1.3 最大Lyapunov指数的估计

Lyapunov指数是刻画耗散体系相空间中相体积收缩过程中的几何特征变化的物理量。Lyapunov指数表示为初值不同的两条相邻轨迹在相空间中随时间推移按指数规律分离的平均发散速率，以定量描述混沌运动初值敏感程度[5]。Wolf[6]认为，对动力系统混沌运动进行判断时，可等价于计算最大Lyapunov指数；若最大Lyapunov指数大于0，表明系统对初值敏感，可判定其运动为混沌状态。

针对最大Lyapunov指数，可由Rosenstein等提出的算法进行计算，该算法对延迟时间、数据长度和噪声的变化等具有较好的鲁棒性[7]。其主要步骤如下：

1）根据延迟时间、嵌入维和式（1）重构相空间；

2）设为不同轨迹上相邻两点之间的距离，则：

式中，C为初始分岔。

找出相空间中一点 X（j）的邻近点 X（j^），则：

3）对相空间中的每一点X（j），计算出该邻近点对的第个离散时间步的距离：

4）lndj（i）-iΔt曲线的斜率便是λ1，即：

式中，〈·〉表示为对所有j求平均。于是，可得最大Lyapunov指数λ1。

2 统计模型与混沌优化BP神经网络融合预测模型

2.1 统计模型

目前，大坝效应量的安全监控模型通常基于坝工理论和数理统计方法采用统计模型、确定性模型和混合模型[8]。大坝监测效应量主要受到库水压力、温度与时效等因素的影响，且影响因素直接互馈作用明显，使得模型建立的精度不高。

通常，混凝土坝的变形按其成因主要由三部分构成：水压因子（δH）、温度因子（δT）和时效因子（δθ），即：

混凝土重力坝的统计模型可表示为：

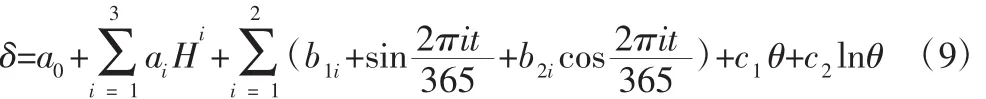
式中，a0为常数项；ai为水压因子回归系数；H为坝前水深；bi为温度因子回归系数，c1，c2为时效因子回归系数；θ=t/100，t为监测日到基准日的累积监测天数。

2.2 BP神经网络预测模型

BP神经网络主要由输入层、隐含层和输出层构成的一种多层前馈神经网络，该网络的主要特点是信号的正向传递和误差反向传播[9]。通过对神经网络的输入输出参数的学习，达到表达函数非线性映射关系的目的。

当采用BP神经网络来预测混沌时间序列时，若一个混沌时间序列的输入为Xi=[x（ti），x（ti+τ），…，x（ti+（m-1）τ）]T，输出为，可选择BP神经网络拓扑结构如图1所示。

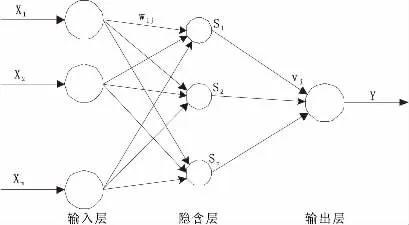
图1 BP神经网络拓扑结构图

BP神经网络隐含层各节点的输入为：

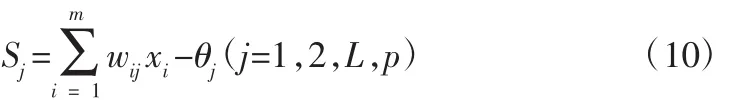
式中，wij为输入层至隐含层的连接权重；θj为隐含层节点的阈值。

BP神经网络隐含层的激励函数有多种表达形式，在此采用Sigmoid函数f（x）=1/（1+e-x），则隐含层节点的输出为：

同理，输出层节点的输入、输出分别为：

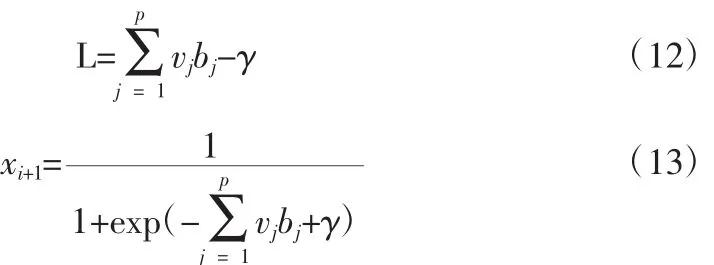
式中，vj为隐层至输出层的连接权值，γ为输出层的阈值。

通过BP神经网络训练求得连接权重wij、vj和阈值θj、γ，最终由式（13）获得模型的预测值。

2.3 统计模型与BP神经网络融合预测模型

统计模型基于坝工理论考虑了变形效应量的物理成因，BP神经网络只是对于非线性函数拟合提供一种智能算法，并未考虑大坝变形观测数据的混沌特性。因此，基于统计模型分离后的变形数据残差序列进行混沌特性识别，对带有混沌特性的数据序列来构建混沌优化BP神经网络融合模型进行大坝变形预测。其主要建模步骤如下：

step1：对变形数据进行统计建模，根据式（9）进行回归计算，可获得统计模型的拟合值、预测值和残差值；

step2：针对变形残差时间序列数据，采用G-P算法、自相关法计算得到的嵌入维数、延迟时间将一维变形时间序列重构为多维相空间，建立混沌优化BP神经网络预测模型；

step3：混沌优化BP神经网络创建并训练后，得到残差序列的预测值，并与统计模型预测值融合得到模型最终预测值。

3 工程实例

以某碾压混凝土重力坝的3#坝段测点水平位移的监测数据为分析对象，选取1010个大坝变形监测时间序列数据作为建模的样本数据，其中将前1000个数据作为训练集，剩下10个数据作为测试集，建立大坝变形统计模型与混沌优化BP融合预测模型，见图2。

图2 大坝测点水平位移方向实测过程线

3.1 模型计算

将训练集的变形监测数据用式（9）建立统计模型，并用统计模型预测测试集的数据，其结果见图3和图4。

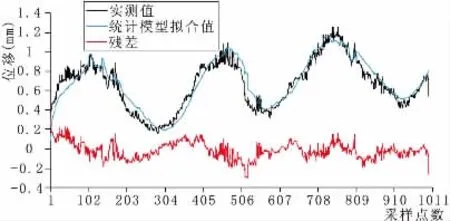
图3 训练集的实测、拟合及残差曲线

图4 测试集的实测与统计模型预测值

关于残差时间序列数据，根据自相关法确定延迟时间为τ=10，并采用G-P算法得到m=7，据此重构相空间。

由式（7）计算得到训练集数据的最大Lyapunov指数λ1=0.0182，可知该训练集的残差时间序列数据具有混沌特性，此时选取的测试集长度为10在允许最大预测时间为1/λ1≈55之内，可进行测试集数据趋势的预测。

3.2 预测结果及性能评价

由组合模型的建模步骤，在MATLAB中编制程序训练，得到BP神经网络的输出。则统计模型与混沌优化BP模型的预测值，具体结果见图5。

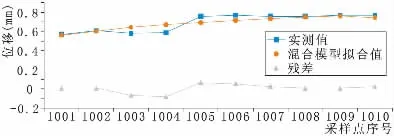
图5 测试集T的实测值、组合模型预测值和残差值

为对模型进行性能评价，选用δMAE，δMSE，R作为定量评价指标。

式中，yi为实测值；为预测值。

将统计模型与混沌优化BP神经网络融合建模与传统的统计模型进行比较，从表1可以看出，统计模型-混沌优化BP的预测精度优于传统统计模型的精度。

表1 两种预测模型的比较

4 结论

（1）根据混沌理论，将大坝的水平位移看成时间序列，进行相空间重构用Rosenstein算法计算得到了实测序列最大Lyapunov指数为正数，可判断系统存在混沌成分。

（2）基于统计模型的不足，通过对大坝变形监测数据统计模型的残差序列进行混沌特性分析，建立了统计模型与混沌优化BP神经网络变融合的预测模型。将该预测模型运用于具体工程实例，表明模型具有比较好的预测效果，可满足实际工程的需要，值得推广。