从一道高三题看向量解法

李国平

(陕西省西安市田家炳中学 710000)

高中数学中的向量知识是一个非常重要的内容.平面向量考题多与三角函数，复数，平面解析几何相结合，同学们又在选修2-1学习了空间向量，而空间向量是解决立体几何中垂直，平行，夹角，距离等问题的有效方法.教材在许多地方也都涉及到向量的应用，同时也是高考考查的热点，然而笔者从多年的教学实践中发现，学生对向量运用和掌握还不能做到得心应手.更有甚者对于使用向量见而生畏，退避三舍，对此笔者在教学中不断渗透向量思想，强化向量意识，强化向量这一工具对解题的影响，强调向量解题的多样性，灵活性，并经常进行一题多解.希望学生重视向量这一工具，强化应用意识.

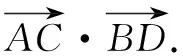
这是一道很平常的题目，但学生拿到之后无从下手，一脸茫然.既不能建系使用向量坐标进行运算，又不知道所求向量的夹角，该怎样做?

学生根据提示，利用向量的加法,减法模仿数量积运算法则，进而求解，尝试如下解法.

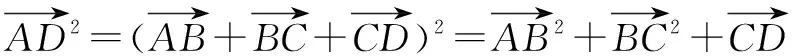
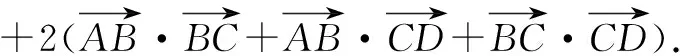
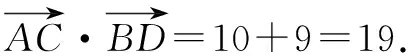
教师点评解法一不错，运用了转化和化归及整体代换思想，将未知问题转换并求解.这个解法虽然可以顺利解出答案,但过程还是比较繁琐.

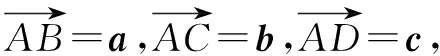
则|a|=2,|c|=7.

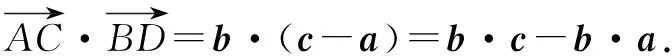
1-2得 -7=4-2a·b+2b·c-49,

∴b·c-a·b=19,

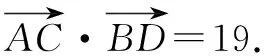
教师点评;解法二通过设定空间向量的一组基底将未知向量转化成已知向量，进而求解，但相对于解法一而言运算更简单，思路更清晰转化更巧妙.

再次引导：该题中我们遇到的关键向量是向量的夹角无一知晓，如果要想知道向量的夹角，除了利用数量积的定义外，还有什么办法可以求某两个边夹角的余弦值呢？(学生马上想到余弦定理)怎么用呢？所给的几条边的长度可以放在哪几个三角形中来使用？这时解法三应运而生.

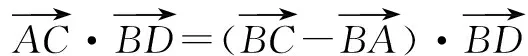
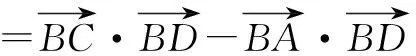
=3BDcos∠CBD-2BDcos∠ABD

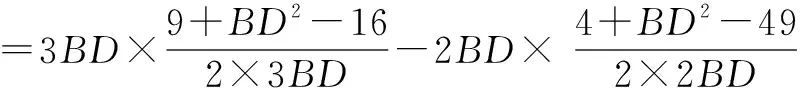
教师点评该解法是将未知向量转化成同起点出发的三个向量的数量积问题，利用余弦定理将未知夹角表示出来，并化简得出结果，同样体现转化和化归思想也是一个很不错的方法， 请大家在还可以继续探究来发现一些更好的做法，与其他同学沟通交流.

后记教学中笔者通过调查了解到许多学生拿到一道向量问题经常无从下手，不是不会做，而是缺乏将学过的向量公式和性质和遇到的问题有机结合在一起的能力.学生缺乏的是分析问题打开思路的方法，作为教师我们要通过设置合理的问题串来引导学生分析问题，抓住问题的实质，切不可直接将整个分析思路过程全盘托出，这样只会适得其反，适时的问题引导，恰当的思维提示，不断鼓励肯定，让学生通过自己的动手实践体会知识和方法生成的过程，遇到相关问题就会水到渠成，逐步达到老师“不教”的目的.通过引导，我们的数学课堂才能充满活力，课堂教学才会高效.