组合双向拍卖协同融合的网格资源分配机制研究

包宋建

(重庆文理学院 电子电气工程学院，重庆 402160)

1 概述

网格技术的发展，使得网格应用的范围从传统的高性能计算和数据密集型应用拓展到更广泛的领域，在计算网格发展的同时，也就出现了其他各种类型的网格，比如数据网格、信息网格等等，随着应用潜力的挖掘，还会出现更多类型的网格。之所以有如此众多的网格出现，其原因是网格技术提供各种资源的普遍共享和分布式协作。

资源种类繁多给网格中资源分配问题带来了极大的挑战，协同资源分配是极其有效的解决办法[1]。网格经济的出现为网格的商业化奠定了基础，采用基于拍卖的资源分配方法实现了同一种资源的高效分配，组合拍卖[2]实现了多种资源共同分配，体现了协同分配资源的思想。在此基础上，本文提出了一种在网格环境下基于组合双向拍卖协同融合的网格资源分配机制，设计了资源分配算法，并通过仿真验证了该算法的性能。

2 组合拍卖理论

组合拍卖(Combinatorial auctions)[3-4]是拍卖的一种，与传统拍卖不同，它是一种竞价人可以对多种商品的组合进行竞价的拍卖方式。组合拍卖适用于买方对商品价值衡量呈现非加性的情况，在分配多种商品时比传统拍卖具有更高的效率。在文献[5]中，作者将组合拍卖分成了一对多和多对一两种，根据每种商品交易的数量又有单单元和多单元组合拍卖之分。

2.1 一对多组合拍卖

一对多组合拍卖有单单元组合拍卖(Single-Unit Combinatorial Auction)和多单元组合拍卖(multi-unit combinatorial auction)[5-6]之分。

在SUCA模式中，仅仅只有一个卖方，他拥有m种待出售的商品，可用集合M={I1,I2,...,Im}表示，每种商品是不可分割的，且数量只有一个。有n个潜在的买方，每个买方对这m种商品的一种或多种感兴趣。B={b1,b2,...,bn}表示买方的竞标集合，买方j的竞标bj=，其中S为商品组合且S⊆M，pj,S是买方j购买该商品组合的竞标价格。

单单元组合拍卖中竞标获胜者决策过程可用模型M1[5]描述：

(1)

(2)

(3)

(4)

其中，xj,S为0-1变量，代表买方竞标获胜与否，获胜时xj,S=1，否则xj,S=0。δj,S=0表示服务组合S不包括商品i；δj,S=1表示商品i属于服务组合S。限制条件式(2)确保一种商品最多分给一个买方，限制条件式(3)保证同一个商品组合不会同时卖给多个买方。式(1)为目标函数，其目的是使卖方在出售商品时获得最大的经济利益。

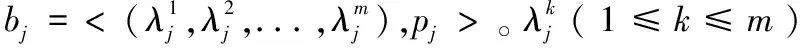
(5)

(6)

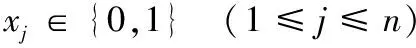
(7)

公式(6)限制了对第k种商品的竞标数量总和需少于提供的数量。

2.2 多对一组合拍卖

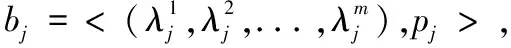
(8)

拍卖模型可用模型M3表示：

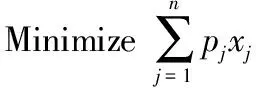
(9)

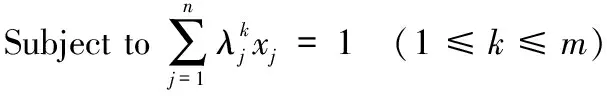
(10)

(11)

公式中变量xj代表竞标成功与否，成功为1，否则为0。限制条件(10)保证买方所有的商品需求都能满足，优化目标(9)使购买商品所花的费用最少。

3 多单元双向拍卖资源分配策略

3.1 系统结构模型

在基于经济机制的网格资源分配过程中，资源提供者首先发布资源的相关属性，比如计算能力、存储能力、在线时间等，而网格用户通过资源发现过程对资源进行筛选，寻找到满足自身任务需求的可用资源。在这种情况下，价格是决定资源分配过程的唯一因素[7-8]。在拍卖模型中，价格主要表现在三个方面，用户的竞标价格、资源的要价标价格以及用户和资源提供者的交易价格，在网格环境中，这些价格都具有动态变化性，因此，在拍卖系统结构中，价格存储功能对竞标者是必不可少的，一方面，可用以存储交易价格，为付费机制提供前提和保障；另一方面，可存储当前竞标价格，作为下一次竞标的参考值，从而实现竞标参与者的决策竞标。同时，文献[9]强调价格策略要体现用户和资源的共同利益，因此，在实现资源分配过程中拍卖商必须具有交易价格确定功能。论文对原有的双向拍卖模型进行了改进，加入了价格存储模块、交易者确定和交易价格确定功能模块，拍卖系统框图如图1所示。

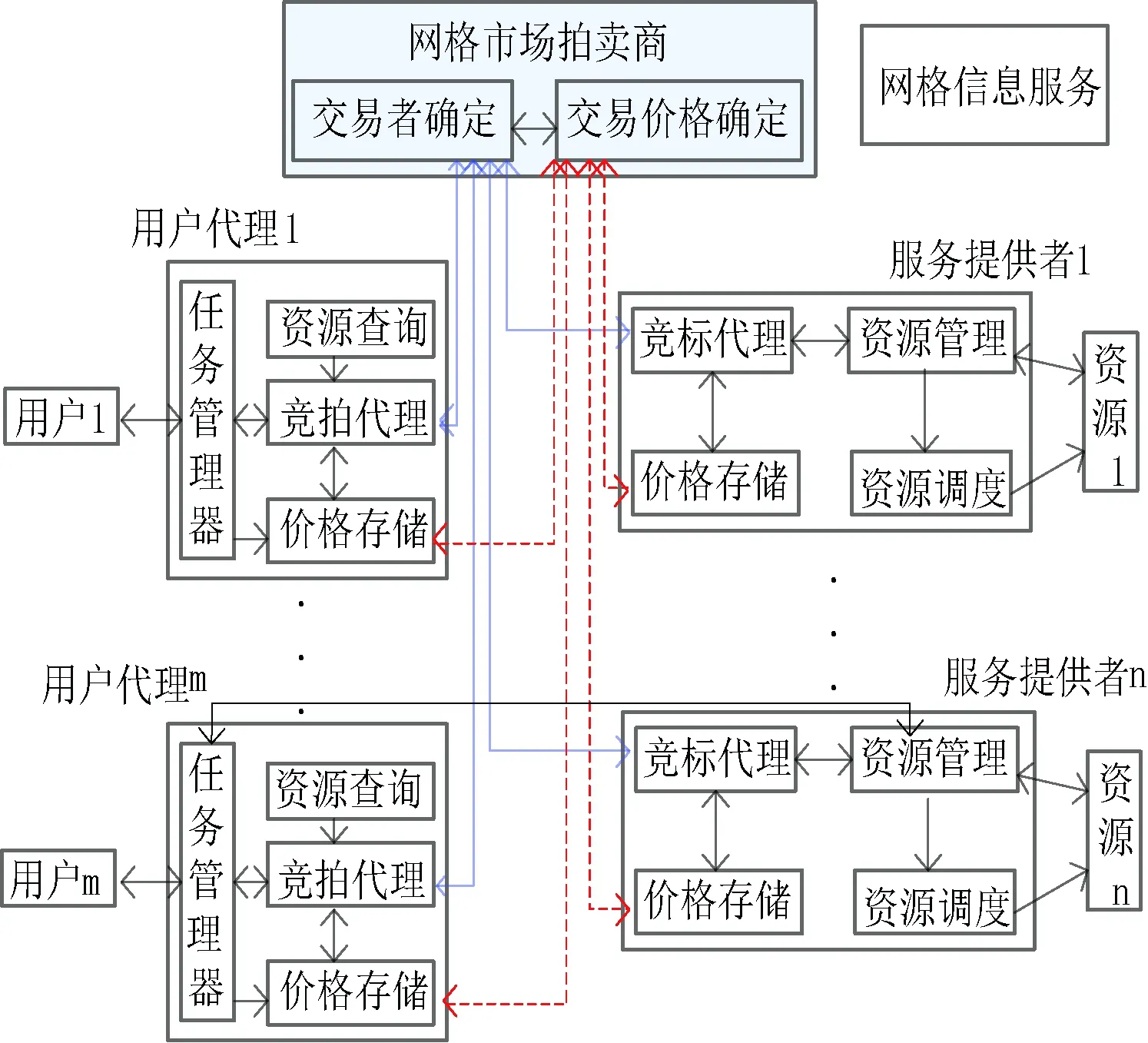
图1 双向拍卖系统组成结构

在该模型中，为降低用户和资源实体与拍卖系统交互的复杂性，双方各自都采用软件代理与系统进行信息交互，通过简单方便的接口为用户提供透明的资源视图。由图可知，系统中主要存在用户代理、服务提供者代理、网格信息服务中心、网格市场拍卖商四类实体。

4 组合双向拍卖协同融合的资源分配机制

4.1 问题描述

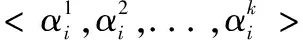
在这种情况下，如何同时兼顾用户和资源提供者共同利益，将这些资源分配给用户使用是一个值得研究的问题，借鉴双向拍卖机制和组合拍卖的思想，采用基于组合双向拍卖的资源协同分配方法来解决这个问题。该方法具有如下优点：

(1)最大化资源提供者的利润，能激发他们贡献闲散的资源，丰富网格中资源的种类和数量。

(2)最小化用户的费用，使其能享受网格带来的便利性和经济性。

4.2 资源分配优化模型

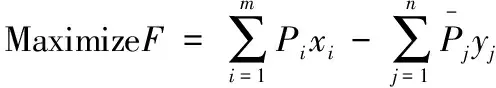
(12)

(13)

(14)

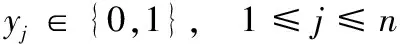
(15)

(16)

(17)

目标函数F使成功交易者竞标价格差最大，表示竞标价格高的用户和要价低的资源提供者成为竞标获胜者，限制条件保证成交的用户所需的各种资源数量都能由资源提供者提供。

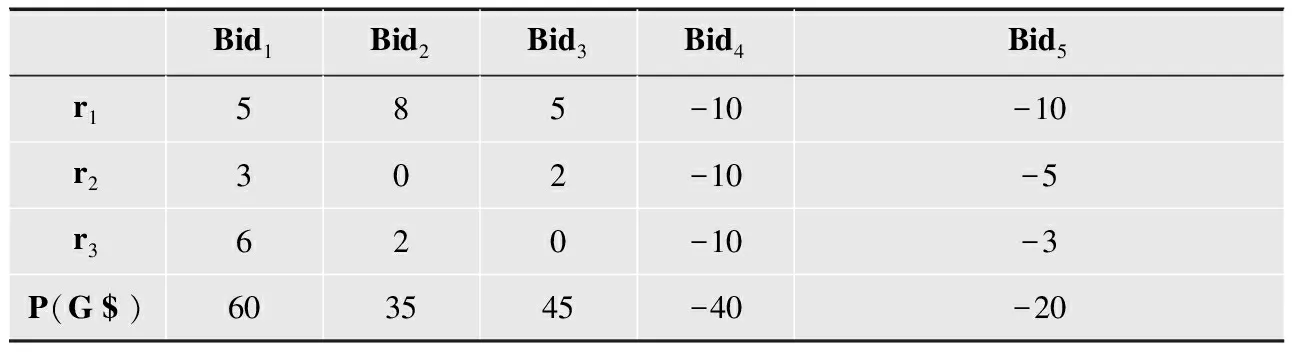
现举例说明上述模型，假设有3种资源，分别为r1,r2,r3，有5个竞标者，包括3个用户和2个资源提供者，他们的资源需求和价格如表1所示。

表11 竞标者竞标参数表

Bid1Bid2Bid3Bid4Bid5r1585-10-10r2302-10-5r3620-10-3P(G$)603545-40-20

则拍卖模型满足：

Maximize60y1+35y2+45y3-40y4-20y5

Subject to 5y1+8y2+5y3-10y4-10y5≤0

3y+2y3-10y4-5y5≤0

6y1+2y2-10y4-3y5≤0

y1,y2,y3,y4,y5∈{0,1}

求解交易者过程就是求解模型中的0-1变量组合的过程。

4.3 定价及资源分配算法

在基于组合双向拍卖的资源协同分配实施过程中，仍采用改进的双向拍卖结构框图，如图1所示。而资源分配及用户应用执行流程为：(1)构建竞标并提交给网格拍卖商，用户构建竞价标，资源提供者构建要价标。(2)确定交易者及交易价格。拍卖商接收到用户的竞价标和资源提供者的要价标后按照预先制定的拍卖准则进行资源分配，并将竞标结果返回给参与拍卖的资源消费者和资源提供者。(3)若竞标成功，用户方提交任务到资源上处理，资源方接收用户的任务进行处理。若竞标成功继续执行步骤(4)，否则转到第(6)步。(4)任务处理完成后，资源提供者将处理结果发送给相应的用户。(5)收到任务处理结果后，用户向资源提供者支付相应的费用。(6)竞标未成功的用户或资源提供者提高竞标价或降低要价重新组织竞标准备参加下一次竞标，即重复步骤(1)。

根据优化模型M4求解出0-1序列yj，确定出后期交易者。这里主要讨论定价及资源分配算法，其步骤详细介绍如下：

(1)首先计算每个交易者的平均报价mpj，见式(19)所示，并将交易者按照买方(UB)和卖方(GSP)进行分类，其中买方按照平均报价由高到低排列得到用户列表bl，卖方按照平均报价由低到高排列得到资源列表sl，然后再将sl按照资源种类进行分类，得到k个卖方列表sli，i∈{1,...,k}，且每个卖方列表对应一个数量列表qi，其中k为资源种类。

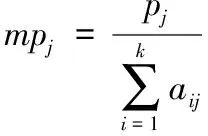
(19)

(2)产生平均交易价格矩阵mtp，其中mtp(s,t)表示bl中第s个买方与sl中第t个卖方进行交易时的平均交易价格，计算公式表示如式(20)。

(20)

(3)按照买方列表bl中的先后顺序进行资源分配及定价，直到所有买方交易者处理完毕为止，由此可以得到资源分配的具体情况以及相应的价格信息。算法伪代码表示如图2所示。

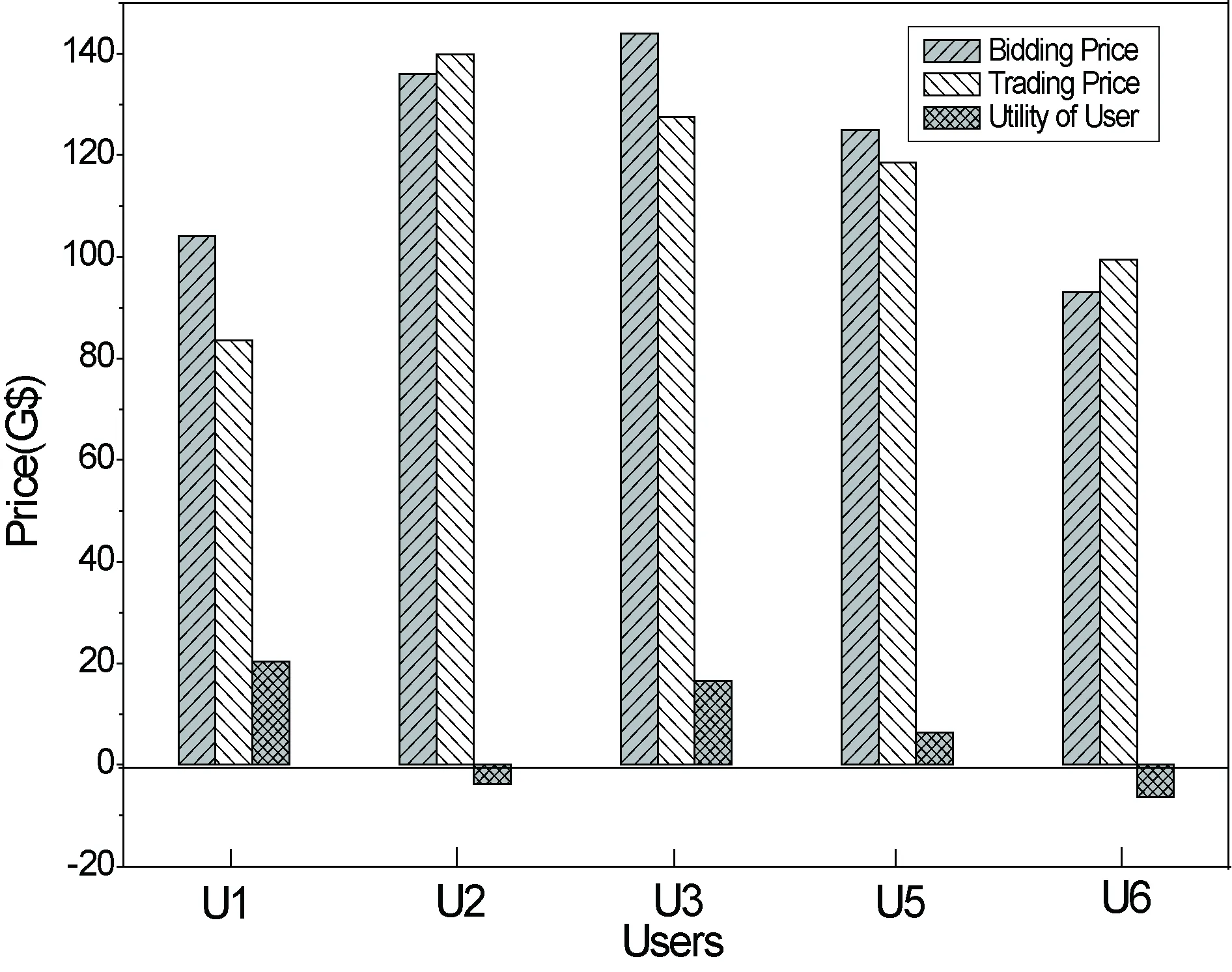
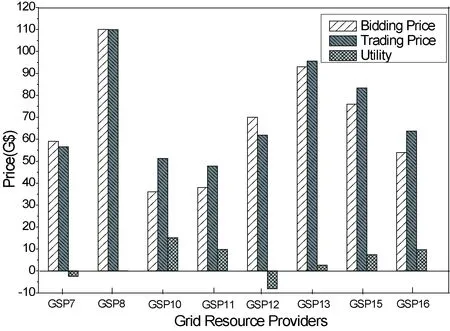
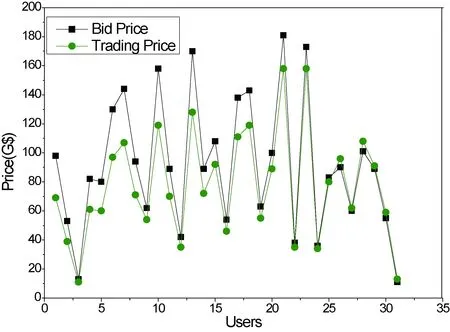
输入：B,bl,sl,sli,qi, 输出：tpi,alloci,0

(1) 初始化：s = 1, i =1, tpi = [0], alloci =[0];

(2) 查询资源种类数量矩阵qi(m)，根据平均交易价格矩阵mtp匹配用户需求

m <-qi中非零量的一个资源的位置

t <-卖方列表sl中销售者sli(m)的位置

If qi(m)≥atbl(s)

tpi (s,t) = tpi (s,t) + atbl(s) *mtp(s,t);

alloci (s,t) = alloci (s,t) + atbl(s);

qi (m) = qi (m) - atbl(s);

atbl(s) = 0;

goto step(3);

else

tpi (s,t) = tpi (s,t) + qi (m)*mtp(s,t);

alloci (s,t) = alloci (s,t) + qi (m);

atbl(s) = atbl(s) -qi (m);

qi (m) = 0;

repeat step(2);

(3) 将分配结果存储到alloci和价格信息tpi中，判断第s个用户需求是否满足

If 资源需求种类和数量都满足

Goto step(4)

Else

i = i + 1; Goto step(2);

(4) 判断是否所有用户需求都满足，分配结束与否

If bl列表已到底

Exit;

Else

s = s +1; i = 1;

更新tpi,alloci,qi;

Goto step(2);

图2 资源分配及定价算法

其中alloci，tpi分表表示第i种资源的分配矩阵和价格矩阵，均为g行h列，分别对应bl以及sl中买方和卖方的个数，alloci表示sl中第t个卖方提供给bl中第s个买方资源的数量，tpi(s,t)表示第t个卖方提供这些数量资源所收取的费用。定价结束后，得到tpb和tps两个矢量分别表示各个买方应支付以及各个卖方应收取的总价格，且有

(21)

(22)

(4)根据资源分配结果将专业分别传给相应的GSP，并按照(3)产生的价格信息进行收费。

5 仿真分析及性能评估

由于GridSim包中仅仅提供对计算资源、存储资源、网络带宽资源的模拟，因此，在未扩展其他资源建模能力时，本节仿真验证过程中只采用这3种资源，为方便描述，假设其代号分别为R1、R2,和R3。系统中设置16个拍卖参与者，其中6个网格用户和10个资源提供者，其参数设置如表2所示。

表12 参与者竞拍参数

网格用户序号服务提供者序号1 2 3 4 5 67 8 9 10 11 12 13 14 15 16R10 4 3 2 410-3-2 -1 -20-3-20-3R23 3 3 0 35 -2-2-3 -3 -2-1-30-3 -1R33 3 4 1 21 -2-3-1 00 -3-1-3-3 -1Price1041361443312593-59-110-80-36-38-70 -93 -71 -76-54

根据优化模型M4可确定竞拍结果，由仿真数据绘制表3与表4，分别代表资源提供者和用户的交易对象及价格。

表13 资源提供者定价结果

卖方交易者序号78101112131516要价59110363870937654交易价56.5109.551.247.861.994.683.463.7支付对象序号2,5,62,3,5,61,33 2,62,3,51,3,51,3,5

表14 交易用户定价结果

交易用户序号竞拍价交易价支付对象:序号(数量+种类,价格)110483.610(3R2,39.5)、 16(1R3,14.1)、15(2R3,30)2136139.813(2R1,3R2,67.2) 、8(2R1,27.4) 、7(1R3,14.2) 、12(1R3,14.3)3144127.610(1R1,11.7)、11(2R1,2R2,47.8)、16(1R2,12.6)、15(1R3,13.5)、13(1R3,13.8) 、8(2R3,28.2)5125118.616(3R1,37)、15(3R2,39.8) 、13(1R1,13.6) 、8(1R3,13.8)、7(1R3,14.3)6938(1R1,2R2,40.6)、7(2R2,28)、12(1R2,1R3,30.8)

由表3和表4可知，同一个资源提供者可以为不同的用户提供服务，比如序号为8的提供者能同时为用户2、3、5、6提供资源，同一种资源也可以提供给不同用户使用，比如提供者15的第3种资源可以分配给用户2个数量给用户1，分配1个资源给用户3。与此同时，用户完成任务所需要的资源种类及数量往往来自不同的提供者，比如表4中为用户3分配的资源来自多达6个提供者，这在一定程度上体现了多个提供者多种资源协同分配的思想。

根据分配及定价结果可分析拍卖策略对用户和资源提供者的效益。不考虑竞标者的竞标策略，假设其均按实际估计报价，对于用户，效益为竞标价与交易价之差，对于资源方，效益为交易价格与竞标要价之差。图3为用户效用估计图。

图3 用户效益分析图

由图可知，用户U1、U3、U5的竞标价格低于交易价格，效用为正，说明资源分配及定价算法能够减少这些用户的费用；同时，U2和U6虽然能够成功交易，但其效用为负值，在一定程度上对这些用户具有不利的一面。之所以会出现这种原因主要是因为算法中按照资源平均价格由高到底进行资源分配，用户U2和U6的单位资源竞标价格分别为13.6和13.3，这在所有成交者中是最低的，因此在分配资源时他们没有优选选择资源的权利，只有将所有竞标价格高的用户分配完毕后才能分配资源，而这些剩余资源往往要价比较高。这也说明了算法体现了交易用户的利益，竞标价格越高效用也越高，具有一定的风险补偿性。

图4 资源提供者效益分析图

图4为资源提供者效益分析图，与用户效益图类似，资源拥有者也有出现负效用的情况，这是由于资源提供者报价太高而没有被用户首先选择的原因造成的。同时，结合竞标参数表和图4可以分析出，资源平均报价越低的资源提供者具有的效益越高，这在一定程度上对资源方的低价出售的行为具有补偿性。

虽然资源分配算法会对用户方或资源拥有者带来负效益，但具有负效用的用户和资源提供者都是竞标价格低和报价高的竞标者，他们往往也是拍卖过程中的淘汰者，在拍卖结果返回时，他们可以根据自身效用情况决定是否进行交易。

为分析在资源分配过程中，交易者亏盈具体情况，进一步验证分配策略的性能，对100个竞标者进行分析，其中用户和资源提供者各占一半，资源种类仍选择3，竞标者参数随机产生。一般情况下，拍卖过程中要价比竞价低，这里，设用户竞标价格在0到200之间，资源提供者要价在0到80之间随机产生。网格中，用户往往需要处理大量任务，需要的资源量比单个资源提供者的数量要多，因此，用户对资源R1、R2和R3的需求量分别介于5到10，10到15，15到20之间；资源提供者对各种资源的提供数量分别介于3到6，6到9，9到12之间。各个竞标者的竞价要价及效益分析如图5和图6所示。

在此次模拟中，一共有31个用户和43个资源提供者进行交易，资源分配成功率为74%。由图可知，在大多数情况下，交易者的效益都为正，表明资源分配方法能够兼顾买卖双方的共同利益。在用户方，仅有6个用户的交易价格略高于竞标价格，而在资源方，几乎所有交易者都具有正效益。同时，也可以看出一般情况下，竞标价格高的参与者往往能获得更大的效用。

图5 用户效用

图6 资源效用

6 结论

首先分析了组合拍卖的基本原理，然后针对网格应用对多种资源协同分配的应用场景需求，将双向拍卖思想与组合拍卖相结合，提出了基于组合双向拍卖的网格资源分配机制，在双向拍卖系统结构模型基础上实现了模型优化，使系统中买卖方的总收益最大化，将交易者确定过程转化为0-1整数规划问题以便求解。同时，给出了相应的定价策略和资源分配策略，该算法考虑竞标者竞标价格形势，能同时兼顾用户和资源提供者的利益，具有补偿性质。最后，通过仿真验证了算法的相关性能，说明了该算法思想具有较高的效率，能提高用户和资源提供者的共同利益。