多个Marshall-Olkin Fréchet分布总体参数在序约束下的极大似然估计
赵春雪,李树有,宓 颖
(辽宁工业大学理学院,辽宁 锦州 121001)
1 预备知识

(1)
对应的概率密度函数为
(2)
设X1,X2,…,Xk是Marshall-Olkin Fréchet分布总体的一个样本.结合已知的概率密度函数(2),可以求得其似然函数为
(3)
因而其对数似然函数为

(4)
2 Marshall-Olkin Fréchet分布参数的极大似然估计
2.1 当已知β和δ时α的极大似然估计
考虑当参数β和δ已知而α未知时,α的极大似然估计.对公式(4)中的α求导得
(5)
令(5)式等于零,易知此方程为非线性方程,很难得到α的显示解.利用Newton迭代法[5],由下面迭代公式可以得到α的估计值:
(6)
文献[6]给出了喷气式飞机空调系统连续故障间隔时间.X代表飞机空调系统的连续故障间隔时间,分别为23,261,87,7,120,14,62,47,225,71,246,21,42,20,5,12,120,11,3,14,71,11,14,11,16,90,1,12,52,95.X服从Marshall-Olkin Fréchet分布.

2.2 当已知δ时α和β的极大似然估计
这里考虑参数δ已知而α和β未知时,α和β的极大似然估计.对公式(4)中的α和β分别求偏导,令其为零得到
(7)
令
则有:
(8)
(9)
(10)
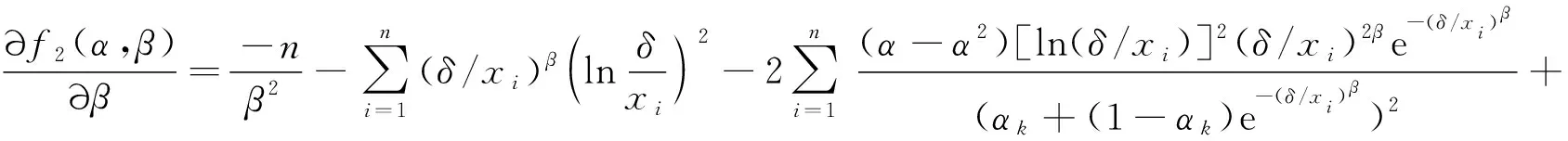
(11)
由Newton迭代法,得到迭代公式

2.3 α,β和δ的极大似然估计
考虑参数α,β和δ未知时,α,β和δ的极大似然估计.对公式(4)中的α,β和δ分别求偏导,并令其为零得
令
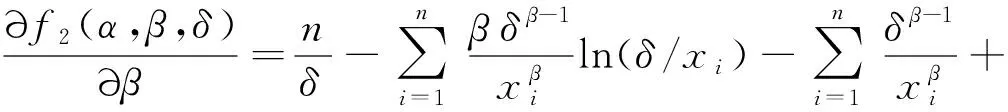
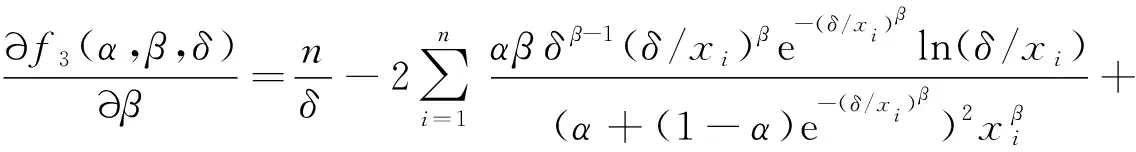
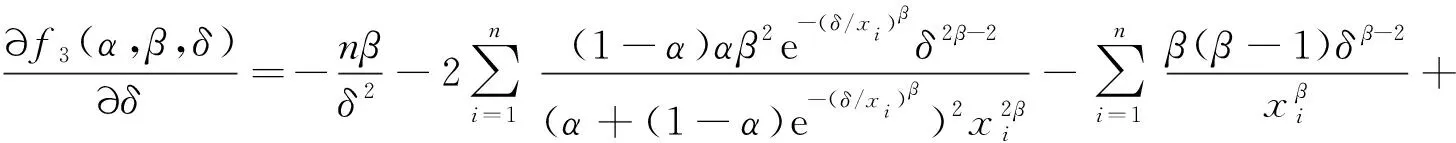
由Newton迭代法,得到迭代公式
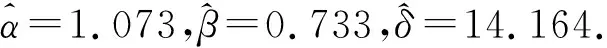
3 多个分布总体参数在序约束条件下的极大似然估计

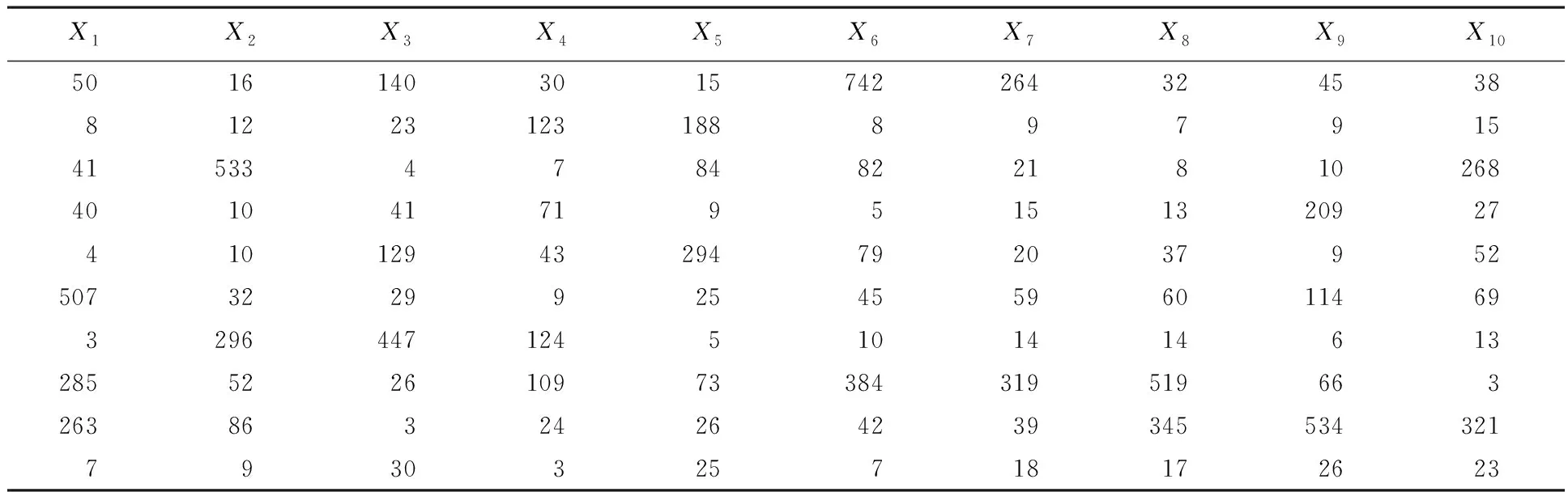
表1 利用MATLAB软件对参数已知的Marshall-Olkin Fréchet分布抽取的随机数
3.1 简单半序α1≤α2≤…≤α10
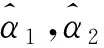
在简单半序约束的情况下可得X1的故障率最高,X5,…,X8的故障率相同,X10的故障率最低.即保证每一批次空调系统的故障率都不高于上一批次空调系统的故障率.
3.2 简单树半序:α1≤αi(i=2,…,9,10)

在简单树半序约束的情况下可得X10的失效率最低,X1的失效率最高.即保证后生产的空调系统的失效率不高于第一批生产的空调系统失效率.
3.3 简单环半序α1≤αi≤α10
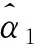
在简单树半序约束的情况下可得X10的失效率最低,X1的失效率最高.即保证最后一批生产的空调系统的失效率最低,第一批生产的空调系统失效率最高.
3.4 伞型半序α1≤α2≤…≤α5≥…≥α10
当空调系统的故障率达到一定程度时,生产者的关注度不仅限于故障率,还需要考虑成本与环保等其他因素.成本的降低有可能导致故障率的升高,因此需要寻找最优解从而达到利益的最大化.此时考虑伞型半序的约束情况.
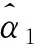
由伞型半序约束可得X1到X4的失效率逐渐降低,X5的失效率最低,继续降低成本或考虑其他因素会导致故障率的升高,从而X5可以达到利益的最大化.

