李color三系的导子、广义导子和拟导子
张 健,曹 燕
(哈尔滨理工大学理学院,黑龙江 哈尔滨 150080)
1 预备知识
文献[1]研究了李color代数的广义导子.文献[2-4]讨论了李三系的广义导子、Jordanθ-导子和广义Jordan导子.李超三系和李超代数的广义导子的结论在文献[5-6]中得以推广.文献[7]给出了李color三系的定义.李color三系是李三系和李三超系的推广,从而一个自然的问题被提出,即李三系上的一些结果能否推广到李color三系上.文献[8]研究了李color三系导子的一些结果,本文在其基础上给出了李color三系的导子、广义导子和拟导子的一些结果.
本文中F表示特征不为3的任意域.
定义1.1[1]设G是交换群,F是任意域.映射ε:G×G→F{0}称为G的斜对称双特征标(或交换因子),如果∀α,β,γ∈G,都有下列三个等式成立:
ε(α,β)ε(β,α)=1,
ε(α,β+γ)=ε(α,β)ε(α,γ),
ε(α+β,γ)=ε(α,γ)ε(β,γ).
在本节中,如果x,y,z是G-阶化向量空间中的齐次元,则以|x|,|y|,|z|∈G表示它们的次数.为方便起见,用ε(x,y)代表ε(|x|,|y|),用ε(x,y+z)代表ε(|x|,|y|+|z|),以此类推.此外,符号ε(x,y)若出现便意味着x,y是齐次元.
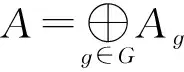
[Aɡ,Aɡ′]⊆Aɡ+ɡ′,∀ɡ,ɡ′∈G,
[x,y]=-ε(x,y)[y,x],∀x∈A|x|,y∈A|y|,
ε(z,x)[x,[y,z]]+ε(x,y)[y,[z,x]]+ε(y,z)[z,[x,y]]=0,∀x∈A|x|,y∈A|y|,z∈A|z|.
对任意x,y,当ε(x,y)=(-1)|x||y|时,李color代数成为李超代数;当ε(x,y)≡1时,李color代数成为李代数.因此,李color代数是一类包含李代数和李超代数的更广泛的代数结构.

(1) [x,y,z]=-ε(x,y)[y,x,z];
(2)ε(z,x)[x,y,z]+ε(x,y)[y,z,x]+ε(y,z)[z,x,y]=0;
(3) [u,v,[x,y,z]]=[[u,v,x],y,z]+ε(u+v,x)[x,[u,v,y],z]+ε(u+v,x+y)[x,y,[u,v,z]],∀x,y,z,u,v∈T.
则称T是color三系.
对任意x,y,当ε(x,y)=(-1)|x||y|时,李color三系成为李三超系;当ε(x,y)≡1时,李color三系成为李三系.因此,李color三系是一类包含李三系和李三超系的更广泛的代数结构.

Endθ(T)={D∈End(T)|D(Tμ)⊆Tθ+μ,∀μ∈G}.
[Dθ,Dμ]=DθDμ-ε(θ,μ)DμDθ,∀Dθ,Dμ∈End(T).
直接验证可知关于此方括号乘法,End(T)是一个李color代数.
定义1.4[7]设T是域F上的李color三系,D∈Endθ(T),其中θ∈G.如果
D([x,y,z])=[D(x),y,z]+ε(θ,x)[x,D(y),z]+ε(θ,x+y)[x,y,D(z)],
∀x,y,z∈T,则称D是T的次数为θ的导子.
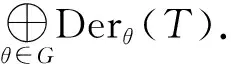

[D(x),y,z]+ε(θ,x)[x,D′(y),z]+ε(θ,x+y)[x,y,D″(z)]=D‴([x,y,z]),
∀x,y,z∈T,则称D是T的次数为θ的广义导子.若存在D′∈Endθ(T),满足
[D(x),y,z]+ε(θ,x)[x,D(y),z]+ε(θ,x+y)[x,y,D(z)]=D′([x,y,z]),∀x,y,z∈T,
则称D是T的次数为θ的拟导子.
令GDerθ(T)为T的所有次数为θ的广义导子的集合,QDerθ(T)为T的所有次数为θ的齐次拟导子的集合,这里θ∈G,定义


Cθ(T)={D∈Endθ(T)|[D(x),y,z]=ε(θ,x)[x,D(y),z]=
ε(θ,x+y)[x,y,D(z)]=D([x,y,z])},
∀x,y,z∈T.令
QCθ(T)={D∈Endθ(T)|[D(x),y,z]=ε(θ,x)[x,D(y),z]=ε(θ,x+y)[x,y,D(z)]},


2 主要结果
定理2.1设T是李color三系,则下面结论成立:
(1) [Der(T),C(T)]⊆C(T);
(2) [QDer(T),QC(T)]⊆QC(T);
(6) G中不存在这样的4-三角8-点v,使得v关联3个(3,3,8)-面和一个(3,4-,8)-面。
(3) C(T)⊆QDer(T).
证明(1) ∀Dθ∈Derθ(T),Dμ∈Cμ(T),∀x,y,z∈T,有
[DθDμ(x),y,z]=Dθ([Dμ(x),y,z])-ε(θ,μ+x)[Dμ(x),Dθ(y),z]-
ε(θ,μ+x+y)[Dμ(x),y,Dθ(z)]=
DθDμ([x,y,z])-ε(θ,μ+x)ε(μ,x)[x,DμDθ(y),z]-
ε(θ,μ+x+y)ε(μ,x+y)[x,y,DμDθ(z)].
且
ε(θ,μ)[DμDθ(x),y,z]=ε(θ,μ)Dμ(Dθ([x,y,z])-
ε(θ,x)[x,Dθ(y),z]-ε(θ,x+y)[x,y,Dθ(z)])=
ε(θ,μ)DμDθ([x,y,z])-ε(θ,x)ε(μ,x)ε(θ,μ)[x,DμDθ(y),z]-
ε(θ,x+y)ε(μ,x+y)ε(θ,μ)[x,y,DμDθ(z)].
故
[[Dθ,Dμ](x),y,z]=DθDμ([x,y,z])-
ε(θ,μ)DμDθ([x,y,z])=[Dθ,Dμ]([x,y,z]).
同理,
[[Dθ,Dμ](x),y,z]=ε(θ+μ,x)[x,[Dθ,Dμ](y),z]=
ε(θ+μ,x+y)[x,y,[Dθ,Dμ](z)].
因此[Dθ,Dμ]∈Cθ+μ(T),于是有[Der(T),C(T)]⊆C(T).
结论(2)的证明类似结论(1),此处略去.
(3) ∀Dθ∈Cθ(T),∀x,y,z∈T,有
Dθ([x,y,z])=[Dθ(x),y,z]=ε(θ,x)[x,Dθ(y),z]=ε(θ,x+y)[x,y,Dθ(z)].
定理2.2设T是李color三系,则QDer(T)+QC(T)=GDer(T).
证明易见QDer(T)+QC(T)⊆GDer(T).
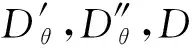
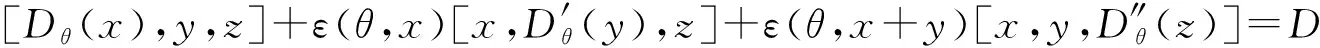
(1)
故

即
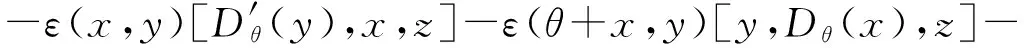
并且

整理得

(2)
将(1)与(2)式相加得
将(1)与(2)式相减得
同理有
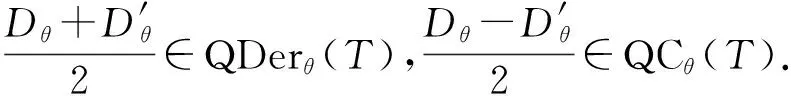
即GDer(T)⊆QDer(T)+QC(T).
定理2.3设T是李color三系,则[C(T),QC(T)]∈End(T,Z(T)).特别地,若Z(T)={0},则
[C(T),QC(T)]={0}.
证明∀Dθ∈Cθ(T),Dμ∈QCμ(T),∀x,y,z∈T,有
[[Dθ,Dμ](x),y,z]=[DθDμ(x),y,z]-ε(θ,μ)[DμDθ(x),y,z]=
Dθ([Dμ(x),y,z])-ε(θ,μ)ε(μ,θ+x)[Dθ(x),Dμ(y),z]=
Dθ([Dμ(x),y,z])-ε(μ,x)Dθ([x,Dμ(y),z])=
ε(μ,x)Dθ([x,Dμ(y),z])-ε(μ,x)Dθ([x,Dμ(y),z])=0.
因此[Dθ,Dμ](x)∈Z(T),[Dθ,Dμ]∈End(T,Z(T)).若Z(T)={0},易知[C(T),QC(T)]={0}.

