臭氧发生器开关电源移相控制策略研究

贺 俊， 王子豪

1.上海矩奉电机自动化有限公司 上海 200331 2.上海电机学院 电气学院 上海 201302

1 研究背景

臭氧因其独特的物理和化学性质，被广泛应用于生活的各个领域，被世人喻为绿色消毒产品。现阶段，相关臭氧产品已经从饮用水处理系统拓展到污水处理、污染气体处理、空气净化、空间杀菌及工业漂白等各个领域。

臭氧发生器电源的性能在很大程度上决定了设备的工作效率及可靠性。若开关电源采用传统的比例积分微分（PID）控制方法，则参数在整定时以对象特性为基础，较为依赖传递函数，而由于臭氧发生器负载属于非线性负载，因此难以对其准确进行数学建模。

相比于其它控制方法，模糊自整定PID控制方法可以根据控制量的变化误差及误差变化率，对控制参数进行自动调整，使控制系统品质保持在最佳范围内［1-3］。

笔者首先通过MATLAB软件进行建模仿真，证明控制算法及电路拓扑的可行性，以及使用模糊自整定PID移相控制策略的系统控制效果优越性，然后使用T MS320F28335型数字信号处理器（DSP）实现系统的控制算法［4］。

2 开关电源移相控制原理

在众多臭氧发生设备中，介质阻挡放电法是目前制备臭氧的主流方法。笔者设计的臭氧电源采用介质阻挡放电工作方式，以臭氧管作为负载，工作过程为：开关电源接入工频交流电，经过不可控整流电路及功率因数校正电路后，输出400 V直流电；再经过全桥逆变电路及变压器升压，输出峰值电压为2 k V、开关频率为12 k Hz的交流电，作用在臭氧管的负载上，串联谐振电感使负载工作在恒流谐振状态。

笔者主要研究开关电源的移相控制，其原理如图1所示。假设输入为经过功率因数校正的400 V直流电，负载部分为臭氧管负载的等效电路，具体理论数值可参考文献［5-6］。移相控制的原理为：通过控制对角开关（QA和QD、QB和QC）同时开通的时间，来调整负载电流的大小。控制对角开关同时开通时间的方法有很多，考虑到软开关的实现条件［7］，笔者选择固定占空比、错开移相角的方法，即QA和QD的开关占空比都为50%，但是开通的时间不一样，QD延时打开，最大延时量为QA波形的半个周期。

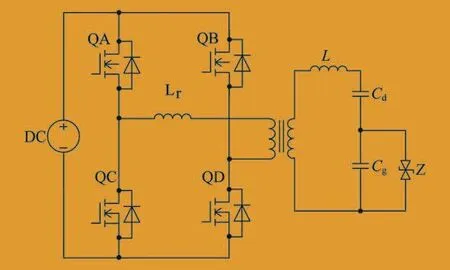
图1 电源移相控制原理

3 MATLAB仿真

笔者采用模糊自整定PID移相控制方法，即在PID控制的基础上进行实时参数优化。反馈控制系统原理如图2所示。

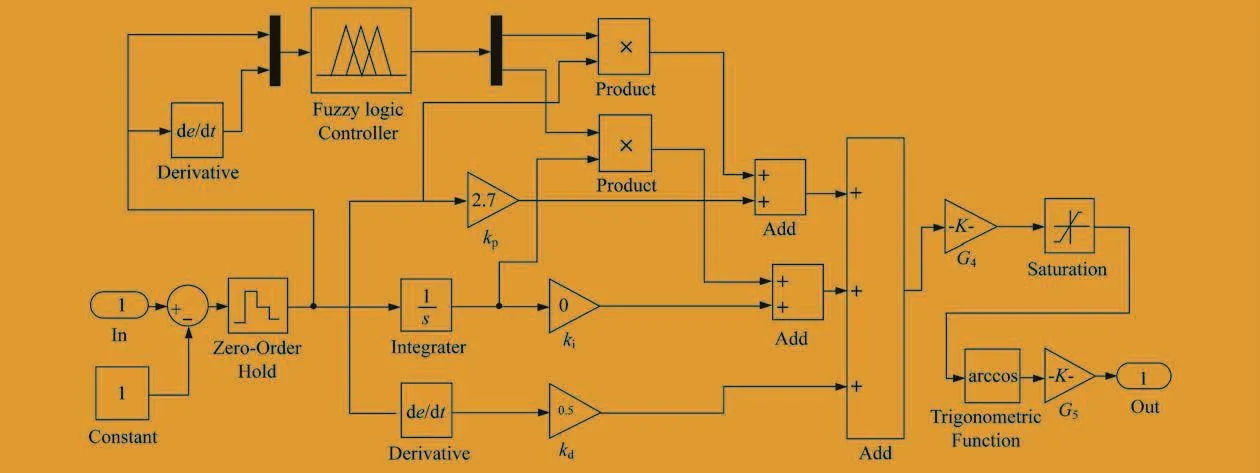
图2 反馈控制系统原理

传统的控制步骤为：测算出电流的有效值，输入反馈控制模块，与给定目标值比较，计算出误差e。为了模拟实际控制器控制效果，Zero-Order Hold模块使连续信号转换为离散数值，送入PID计算环节。一个闭环仿真周期设为0.1 ms，即电流的有效值每0.1 ms更新一次。kp、ki、kd为PID控制初始因数。误差e与移相角θ之间的传递函数为：

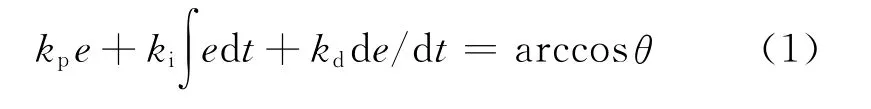
移相角θ与移相时间，也即开关延时t之间的关系为：

式中：T为一个开关周期。

传递函数arccos的自变量取值为［－1，1］，所以要对计算输出值进行线性缩小，限幅Saturation为［－1，1］，最终输出Out为超前桥臂与滞后桥臂之间的延时。

在实际臭氧发生器的工作过程中，臭氧管的负载会因工作时间的增加及温度的变化而受到干扰因素的影响，对象参数特性会发生改变。加入参数模糊自整定的方法，可以使控制系统品质指标保持在最佳范围内。通过对不同工作状态时误差e与误差变化率ec进行模糊推理，得出PID三个参数的校正。笔者仿真采用比例积分（PI）参数自整定，仅调整比例因数kp和积分因数ki，减小计算量，加快系统的响应速度，使系统更适合用于工业生产的实现和推广。

4 比例与积分因数整定原则

4.1 比例因数

由于定义误差为实际的电流值减去参考值，因此当误差e为负值时，系统的电流低于目标值。当e为正值时，系统处于超调状态。误差变化率ec为正值时，表示电流处于上升阶段。ec为负值时，电流处于下降阶段。将误差e和误差变化率ec的值分为7档——NB、NM、NS、Z、PS、PM、PB，依次代表负大、负中、负小、零、正小、正中、正大。

在闭环控制过程中，先设定一个初始比例因数kp0。当响应在上升过程中误差较大，即e为NB、NM时，比例因数的变化量Δkp取正值，增大比例因数以尽快消除误差，根据ec的大小调整不同大小的Δkp。与此相对应，当系统超调较大，即e为PB、PM时，Δkp取负值，减小比例因数使目标值尽快回落［8-9］。

当误差在零附近，即e为Z时，分三种情况：①ec为P时，电流仍然处于上升状态，此时Δkp取负值；②ec为N时，电流处在下降状态，Δkp取正值；③ec为Z时，说明实际的电流值和目标值很接近，并且较为稳定，所以要保持此时的比例因数不变，Δkp取Z。

还有四个状态，选择保持比例因数不变，分别是：①e为NS，ec为PS；②e为 NS，ec为PM；③e为PS，ec为NS；④e为PS，ec为NM。举例说明，当e为NS、ec为PS时，电流实际值小于目标值，但是电流仍然保持小步伐上升的状态，此时不用改变比例因数电流也可以较快达到稳态。这样设计可以减小控制系统的工作量，提高控制系统的稳定性。比例因数模糊规则表见表1。

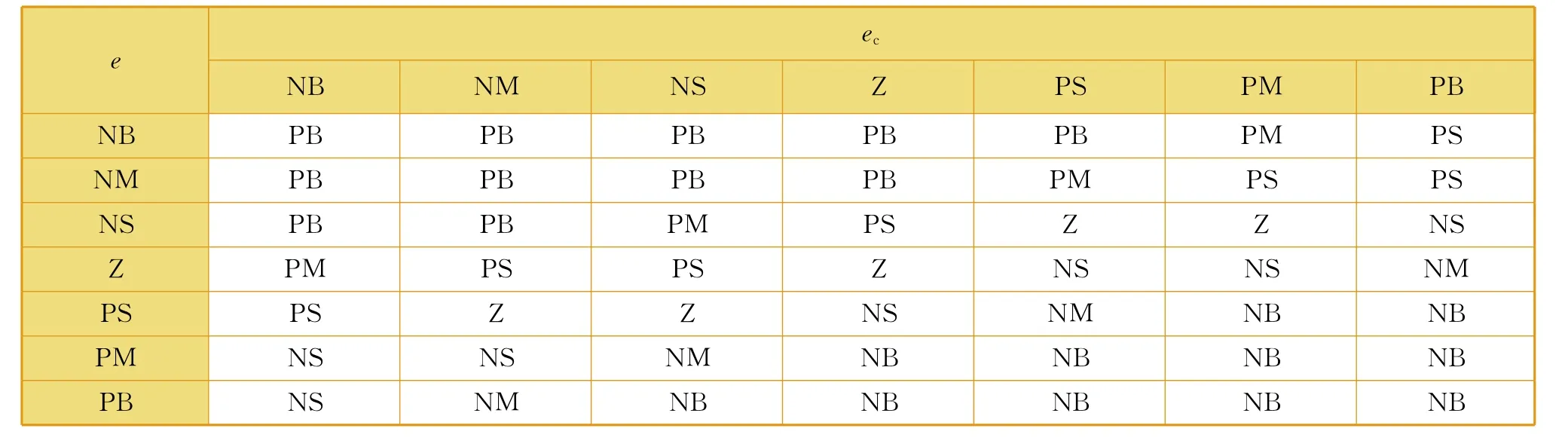
表1 比例因数模糊规则表

4.2 积分因数

积分因数的设定采用积分分离策略，在普通PID控制过程中引入积分环节的目的，主要是为了消除静差、提高控制精度。但是在系统启动和停止的过程中，短时间内会产生很大的偏差，造成PID运算的积分积累，导致控制量超过执行机构所允许的极限控制量，引起系统产生较大的超调，甚至引发系统较大的振荡。

积分分离策略是当电流值与目标值的误差较大时，取消积分作用，以免因为积分作用使系统稳定性降低。当被控电流值接近目标值时，引入积分控制。设置积分因数的初始值ki0＝0，误差e为Z、NS、PS时，积分因数取正值；否则，积分因数取零［9-10］。积分因数模糊规则表见表2。

在线性运算过程中，控制系统通过对模糊逻辑规则的处理、查表和运算，完成PID参数的在线校正。定义误差e、误差变化率ec的模糊集合均为｛N，Z，P｝，N、Z、P依次代表负、零、正，e的基本论域为［－1，1］，ec的基本论域为［－1，1.5］，kp、ki的模糊集合也是｛N，Z，P｝，kp的论域为［－3，3］，ki的论域为［－1，1］。

图3所示为电路启动到达稳态的过程中负载电流的有效值，虚线表示传统PID控制，kp、ki的初始值分别设为2.7和1。实线表示模糊自整定PID移相控制，kp、ki的初始值分别设为2.7和0，在工作过程中伴随模糊规则而变化。在传统PID控制时，启动过程中电流出现较大超调，在1 ms过后达到稳定，但是存在0.1 A左右的稳态误差。使用模糊自整定PID移相控制方法很好地解决了问题，启动时超调量小，电流很快接近目标值，达到稳态。

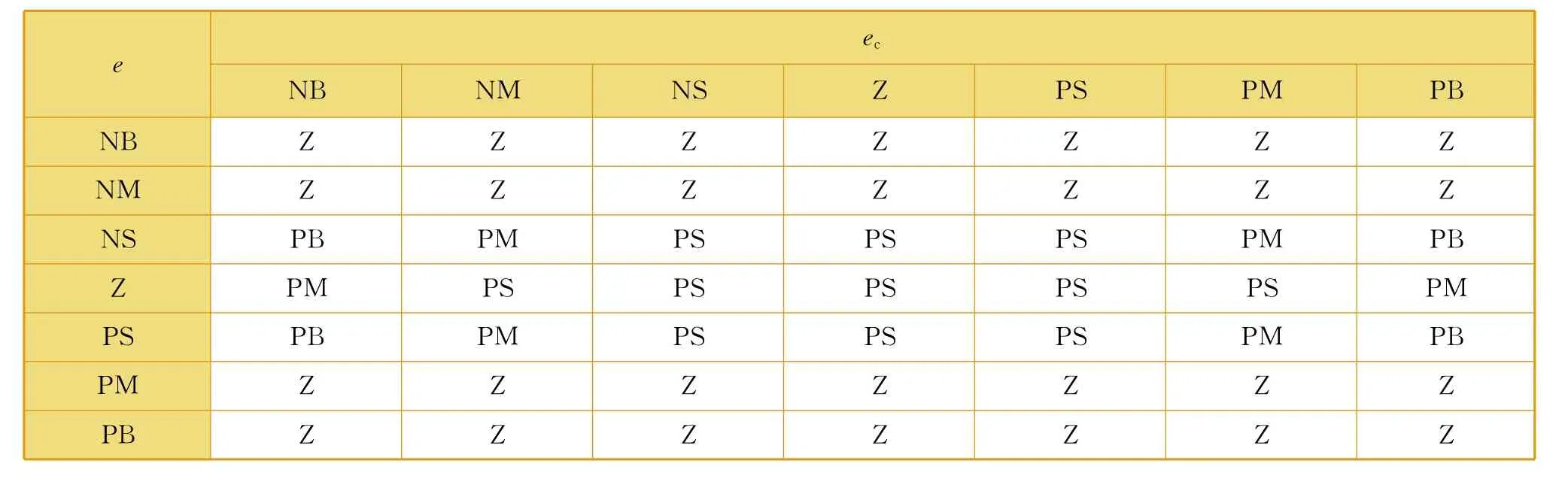
表2 积分因数模糊规则表

图3 启动过程电流有效值

5 基于DSP的控制策略软件编程

5.1 模糊控制查表法

智能控制的硬件实现一直是工业生产中棘手的问题，在很多情况下由于编程复杂、计算时间较长，控制效果达不到预期，使工业生产中简单的PI控制依然占据着主流。DSP和现场可编程门阵列等新一代控制器的迅速发展，大大提升了处理器的运算速度和指令处理速度，使智能控制可以更加广泛地应用于工业生产中。采用T MS320F28335型DSP芯片，作为本次试验的控制器，其系统时钟为150 MHz，采用哈佛结构，能够在一个周期内完成32×32位的乘法累加运算，优异的性能满足本次试验的需求。

模糊控制也是一种经典的智能控制方式，目前主流的实现方法为在线计算法和查表法。在线计算法的优点是程序所占的内存空间小，缺点是计算周期长。查表法恰好相反，不需要实时运算，但是需要较大的储存空间。DSP芯片上有256 KB×16位嵌入式闪存储存器，有充足的空间储存数据，适合使用查表法来实现控制。具体应用时，在MATLAB Si mulink中有系统测试界面，可以计算出模糊控制器一一对应的输入和输出关系，制作出表格。

模糊控制规则为：输入量为误差e和误差变化率ec，根据需求选择取值精度，对应输出值为kp、ki。使用if嵌套的方法对f uzzy（）函数编程：

首先对e进行判断，然后再对ec进行判断。函数返回值为kp、ki，为PID（）函数提供参数。本程序设计精度为0.1，有些工作环境中需要提高模糊精度，势必要增加程序的存储地址，在DSP的随机存储器中可能会无法运行，建议直接在闪存存储器中调试。

5.2 数模转换采样与中断函数

数模转换采样和中断实际是控制闭环周期，如前文所述，闭环周期为0.1 ms，即每0.1 ms进行一次电压采样，与参考值比较，得出e、ec，通过fuzzy（）函数更新kp、ki，代入PID（）函数，更新被控量移相角。

数模转换采用定时器触发，在CPU ti mer0中断里使能数模转换的软件触发位，触发位具体为Adc Regs.ADCTRL2.bit.SOC＿SEQ1＝1。在数模转换初始化函数void ADC＿config（void）中，配置数模转换的采样频率、采样通道数、中断入口、结果排序等。DSP芯片的采样模块有16个采样通道，为了提高采样精度，选择六通道顺序采样后累加求平均策略。

数模转换的原理是DSP可以测量出固定几个引脚上的输入电压，范围是0～3 V，所以负载的电流大小不可以直接测量，需要使用电流互感器将电流按比例缩小，经过二极管整流电路后接在电阻上，电阻两端的电压才可以直接输入数模转换引脚，如图4所示。

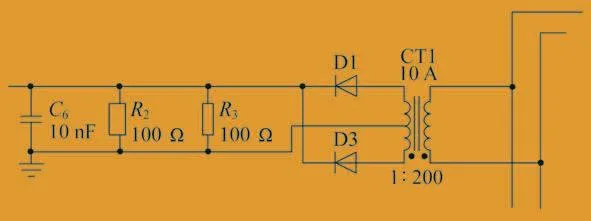
图4 数模转换采样原理

5.3 双桥臂脉宽调制波

本次试验需要用到4路脉宽调制波，即DSP芯片中两个EPWM模块。EPWM1模块输出超前桥臂的波形控制开关管A、C，EPWM2模块输出滞后桥臂的波形控制开关管B、D。系统时钟频率为150 MHz，脉宽调制波控制频率为12 k Hz，等于12 500个系统时钟。模块统一采用Up-Down计数模式，寄存器TBPRD的数值为6 250，移相角θ可通过6 250θ／π转换为时钟周期个数。

EPWM1和EPWM2模块波形分别如图5、图6所示。

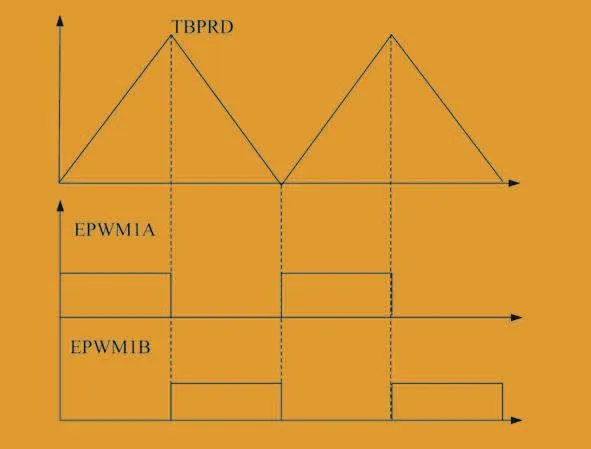
图5 EPWM1模块波形

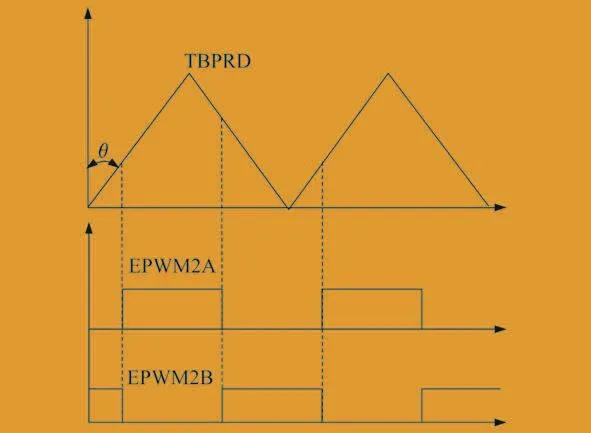
图6 EPWM2模块波形

具体编程如下：

EPwm1 Regs.AQCTLA.bit.PRD＝AQ＿SET；

EPwm1 Regs.AQCTLA.bit.ZRO＝AQ＿CLEAR；

EPwm1 Regs.AQCTLB.bit.PRD＝AQ＿CLEAR；

EPwm1 Regs.AQCTLB.bit.ZRO＝AQ＿SET；

EPwm2 Regs.CMPA.half.CMPA＝YIXIANG；

EPwm2 Regs.CMPB＝6250－YIXIANG；

EPwm2 Regs.AQCTLA.bit.CAU＝AQ＿SET；

EPwm2 Regs.AQCTLA.bit.CBD＝AQ＿CLEAR；

EPwm2 Regs.AQCTLB.bit.CAU＝AQ＿CLEAR；

EPwm2 Regs.AQCTLB.bit.CBD＝AQ＿SET；

EPWM1模块不需要设置比较寄存器数值，在数值寄存器值等于TBPRD和0时，动作模块触发。EPWM2模块CMPA数值为Uint16 YIXIANG，CMPB数值为6250-YIXIANG。

6 试验波形

根据前文的理论分析，笔者设计试制了一台功率为10 k W的臭氧发生器电源样机。

当臭氧发生器电源设备工作达到稳态时，负载两端的电流和电压波形如图7、图8所示。图7中横坐标每格代表30μs，图8中横坐标每格代表40μs。蓝色的电压波形基本呈正弦波形状，臭氧管负载与串联电感经过谐振后负载电压峰峰值稳定在8 k V左右。黄色的电流波形则因为臭氧管本身工作特性有非线性的放电过程，产生了一些形变，不过总体而言还是呈正弦波形周期变化，电流有效值接近0.78 A的目标值。

7 结束语

笔者基于臭氧发生器的开关电源控制策略，对传统PID控制进行优化，通过MATLAB软件仿真确认，模糊自整定PID移相控制更适合臭氧发生器开关电源工作。搭建试验样机实现了整个控制过程，证明笔者提出的控制策略可以在实际生产过程中应用。

图7 移相角90°时负载波形

图8 移相角50°时负载波形