块结构r-循环矩阵的性质及其算法研究
史雨梅, 秦 梅
(上海理工大学 理学院,上海 200093)
循环矩阵的概念于1885年由Muir S.T.首次提出,1950年之前该方面未引起数学研究者的足够重视,直到1950年之后,人们才对其行列式、逆等性质进行研究。近年来,循环矩阵以其良好的性质和特殊的结构,被广泛运用于科技工程及应用数学等领域,如石油勘测、信号处理、数字图像处理、计算机时序分析、优化设计等方向。循环矩阵理论已成为矩阵论的热门研究方向[1-3],并获得了飞速的发展。
由于特殊循环矩阵的性质和结构相对于循环矩阵更为良好,故引起我们的关注,并对其进行了推广和研究,例如其行列式、非奇异性、对角化、谱分解、高次幂的表达式、逆矩阵及广义逆的各种算法等。特殊循环矩阵在研究中所取得的成果对相关领域的发展将起到至关重要的作用。
随着对循环矩阵研究的深入,新的循环矩阵不断被提出[4-6],例如r-循环矩阵、首尾差r-循环矩阵、块循环矩阵等。本文在此基础上,给出了块首尾差r-循环矩阵的概念,研究了其线性运算、矩阵乘积、非奇异性、对角化等性质,并给出了三对角块r-循环线性系统求解的直接算法。
1 预备知识
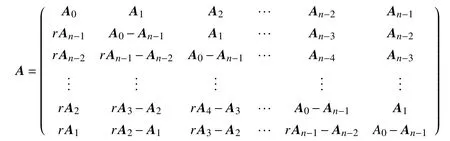
定义2[7]若矩阵和矩阵分 别是和阶的矩阵,则Kronecker积为一个的 矩阵,即


定义3[8]设矩阵,若矩阵的奇异值记作,则的 Schatten范数为

引理1[9]设,且,则有

引理 2[10]若分块多项式矩阵进行一系列的初等
行变换后化为
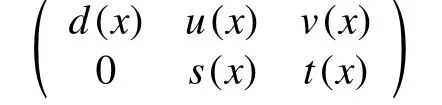
2 块首尾差r-循环矩阵的性质
为了研究方便,称如下形式的矩阵为基本块首尾差r-循环矩阵。
显然,它的特征多项式为
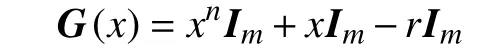
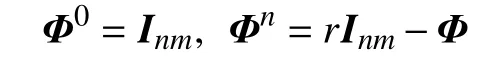
证明:必要性显(然。)
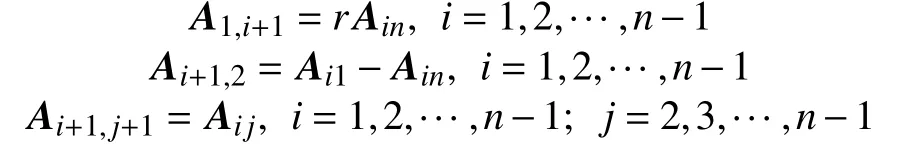
则可得

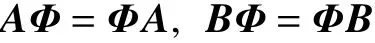
因此

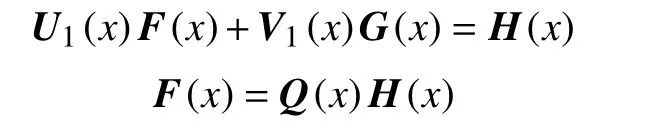

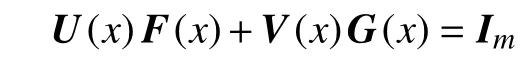

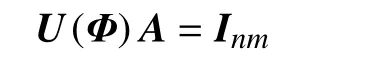
3 块首尾差r-循环矩阵的对角化

且
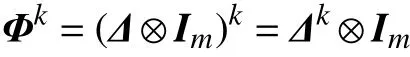
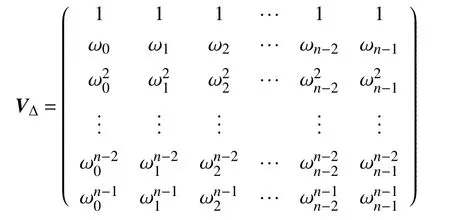
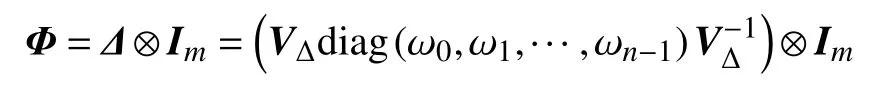
由Kronecker积性质可知
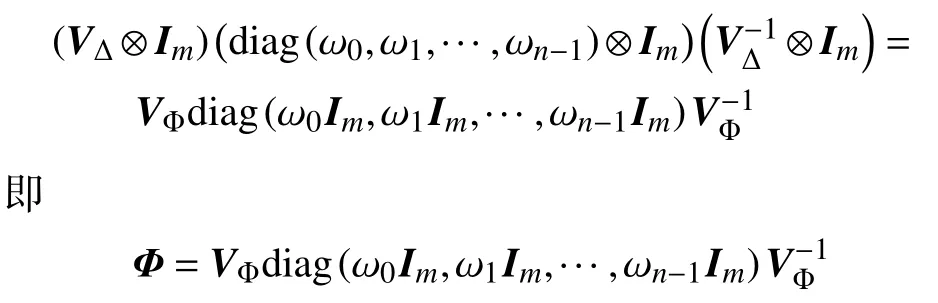
所以
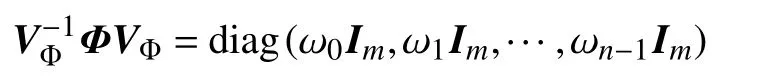
定理1得

所以


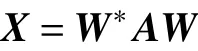
于是

因此
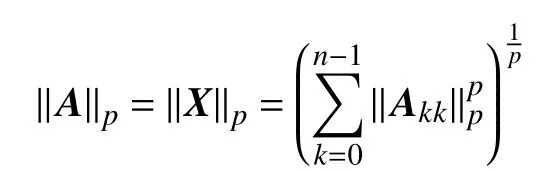

4 三对角块r-循环线性系统解的直接算法
在现代工程研究领域,常常会用到循环线性系统,通过已有的数学理论,下面将对如下具有块结构的Hermitian对称线性系统的解进行研究

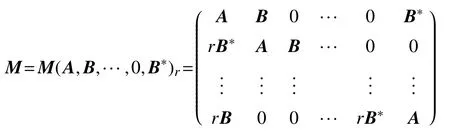
首先考虑方程

其中

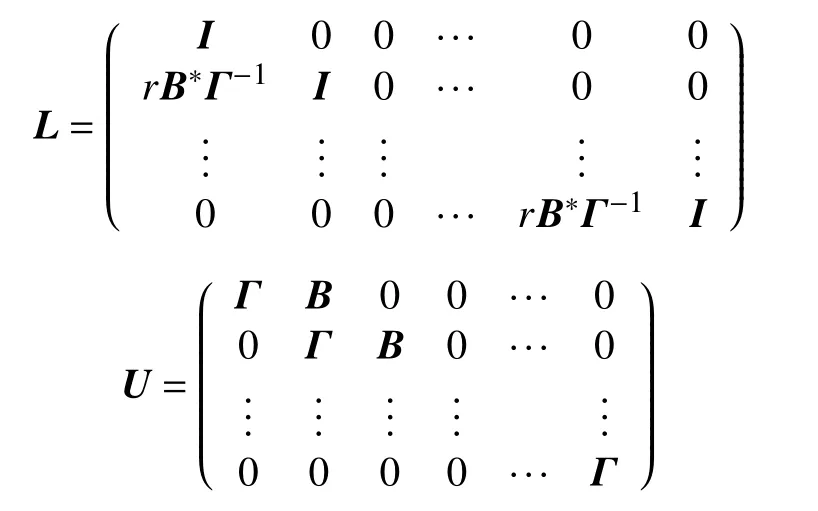

通过计算可得

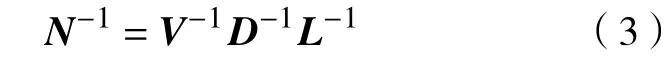

接着寻求如下线性系统的解

这里
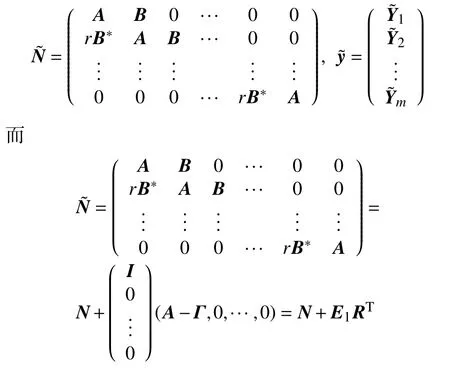
于是由Sherman-Morrison-Woodbury公式得
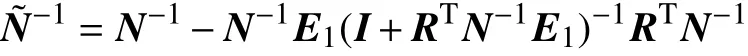
因此,可以得到式(4)的解为

而由式(3)可计算得到

因此,式(4)可写成

最后回归到线性系统(1),寻求该线性系统的解。式(1)的系数矩阵可以写为
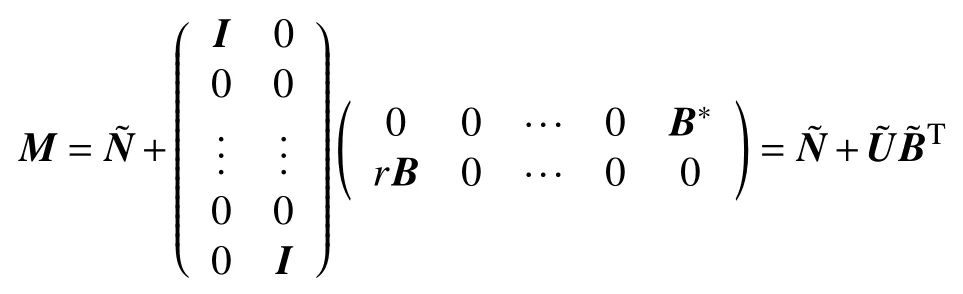
于是再由Sherman-Morrison-Woodbury公式得
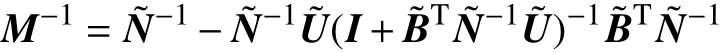
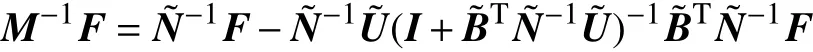
此时线性系统(1)的解为
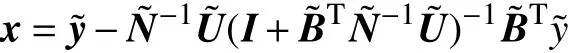
5 结 论
提出了块首尾差 循环矩阵的概念,并验证了其和、差及乘积仍是块首尾差循环矩阵,这说明了其有很强的保结构性。接着通过构造基本块首尾差循环矩阵研究了非奇异性,并通过运用Kronecker积的性质,研究了其对角化的性质。利用Sherman-Morrison-Woodbury公式,给出了三对角块循环线性系统求解的直接算法,这对其他领域的应用具有重要的意义.

