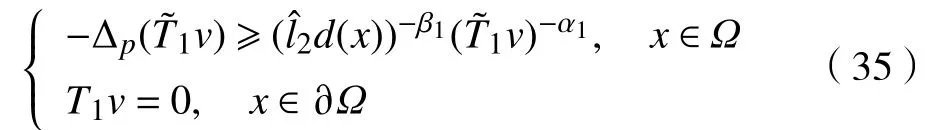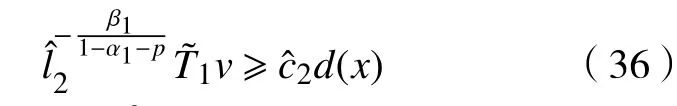一类奇异拟线性椭圆方程组正解的存在性

王雨婷， 贾 高

（上海理工大学 理学院，上海 200093）

1 问题的提出

现代任一学科的发展都必须保证自身的精确化，而建立数学模型是精确化的重要手段之一。在这些数学模型中，会有许多非线性的问题，如p-Laplacian算子在研究化学反应、假塑性流体、种群动力学及天体物理学等问题时就常常被用到。这些问题的解决对于科学技术的发展产生很大的推动作用，同时对数学学科自身的发展也有很大影响。

近些年来很多学者开始研究拟线性椭圆方程及方程组的问题。拟线性椭圆型问题来自于拟正则映射理论和广义反应扩散理论，以及非牛顿湍流等问题。因为，时p-Laplace算子不再是线性算子，所以，关于Laplace算子的线性理论不能直接用于p-Laplace算子。对于拟线性椭圆方程

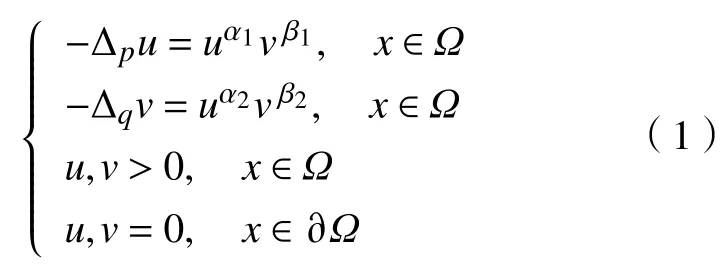
对正则情况（即所有指数都是正的）已经研究得很透彻了。如文献[3]研究了的情况，文献[4]利用上下解理论和Schaulder不动点定理研究了时方程组解的存在性等。

关于方程组（1）的奇异情况是最近开始被研究的。一部分工作致力于研究半线性情况，即。在这种情况下，方程组（1）可以看作是一类与椭圆方程组类似的Gierer-Meinhardt 方程组，是一种重要的生物化学模型，此时可以直接用上下解方法和拓扑度理论研究其解的存在性，如文献[5]。另一部分工作则致力于研究拟线性的情况，即，文献[6-7]分别用单调性方法和上下解理论研究了时方程组（1）解的存在性。而文献[8]研究了所有指数都是负数时方程组（1）解的存在性，这种情形与出现在天体物理学中的Lane-Emden方程有关，具有重要的应用背景。

现考虑奇异拟线性方程组

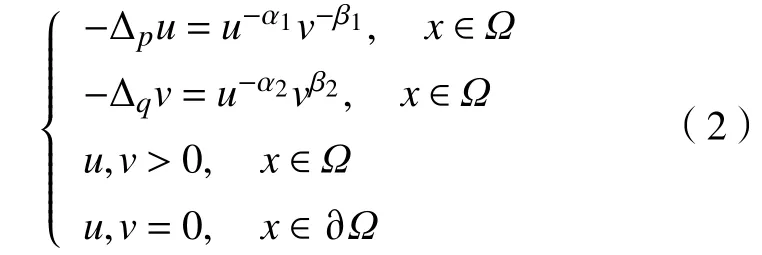
2 预备知识

现在考虑边值问题

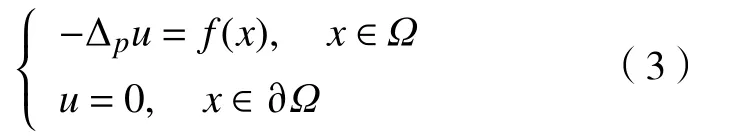
引理1[9]，对是的共轭指数，， 则即 方程（3）只。有一个弱解，即对，有

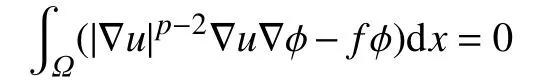
引理2[9]设是一个有界区域，那么，

引理3[9]设，，满足

引理4[10]若，是摄动函数，是区域的直径，，，那么，对于

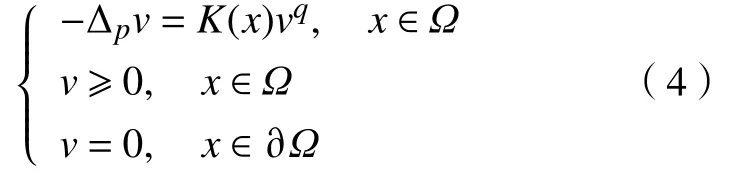
，且满足

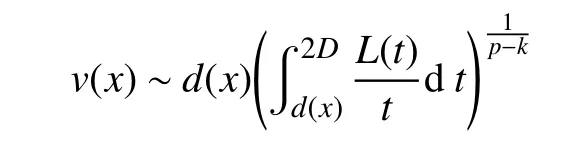
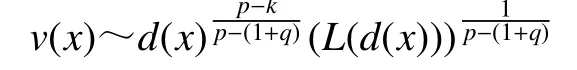
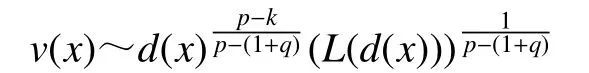
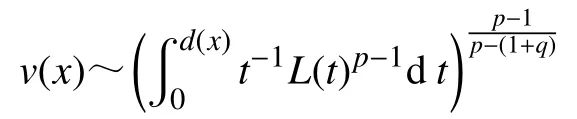
引理5[11]若是的弱解，，，

3 主要结果的证明

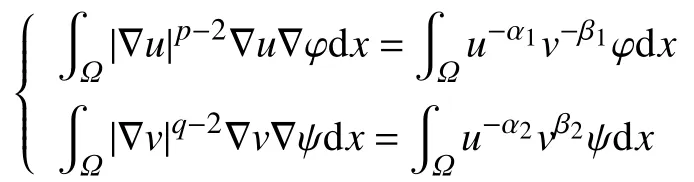
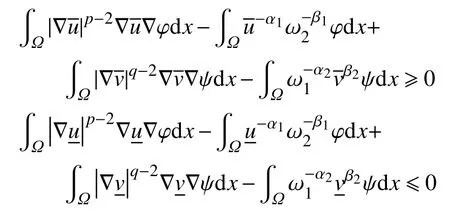
现证明定理1。分别对2种情况进行讨论。

对方程

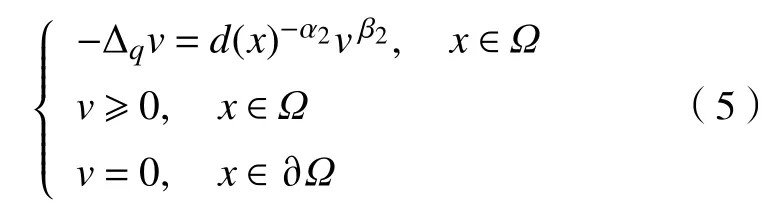
由引理4可得其上、下解满足

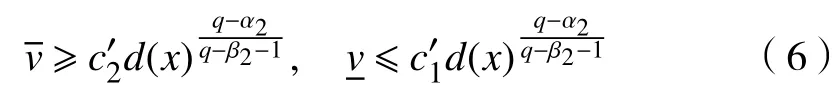
进一步，对方程

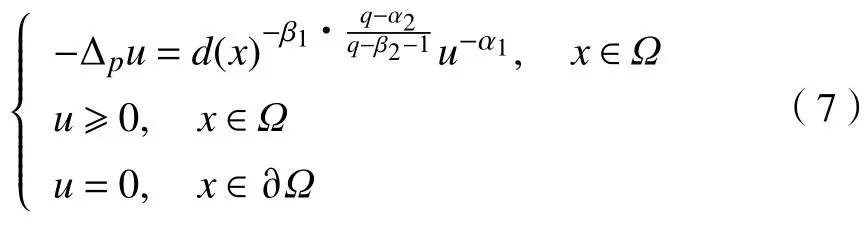
利用引理4可得式（7）的上、下解满足

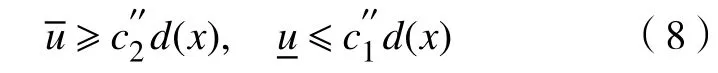
取

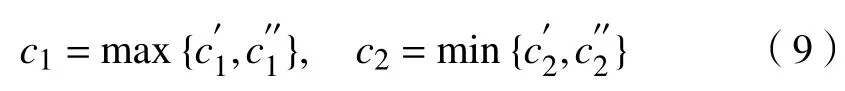
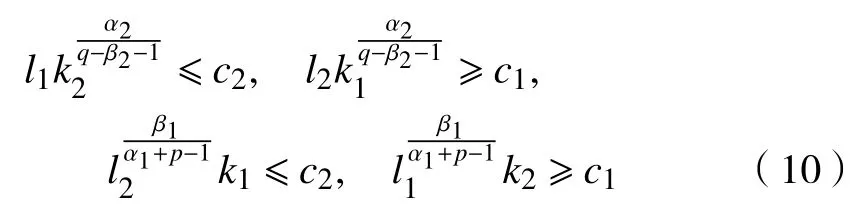
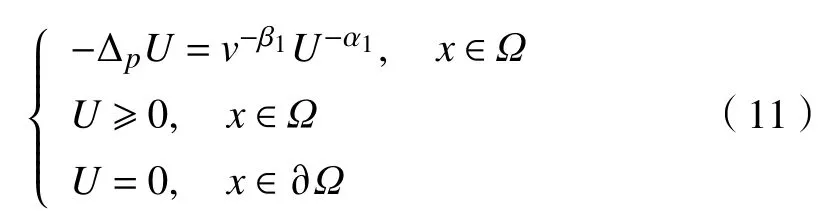
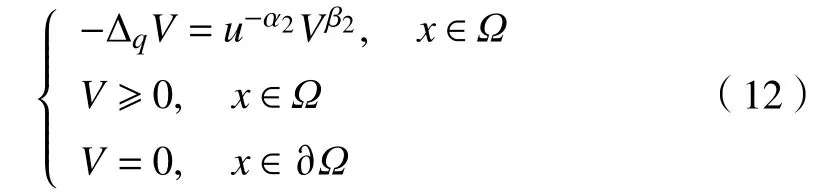
定义算子 如下：

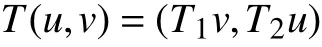
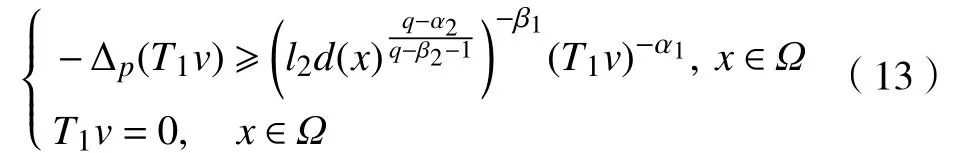
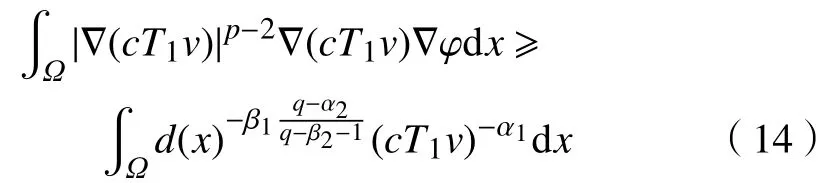
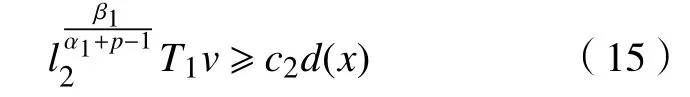
从而由式（10）可得

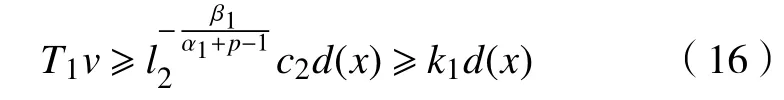
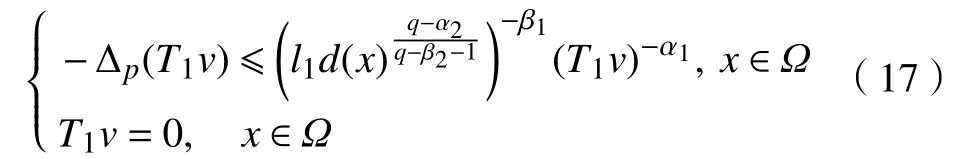
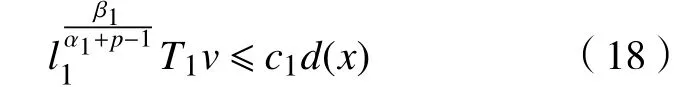
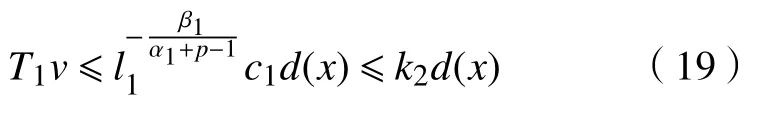
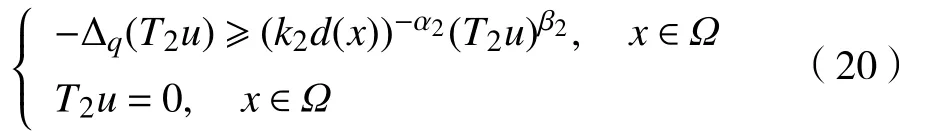
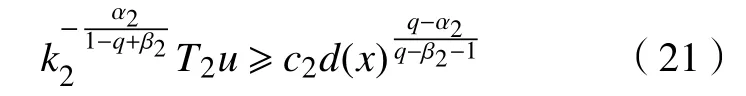
由式（10）就可以得到

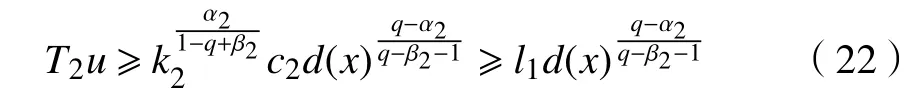
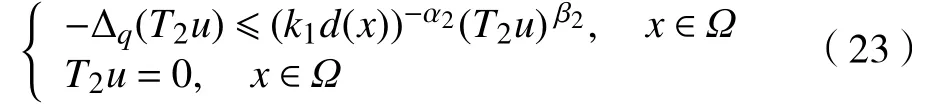
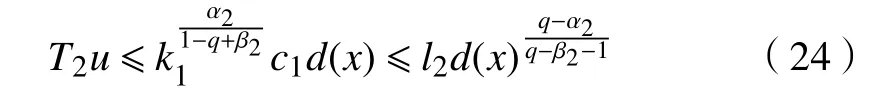
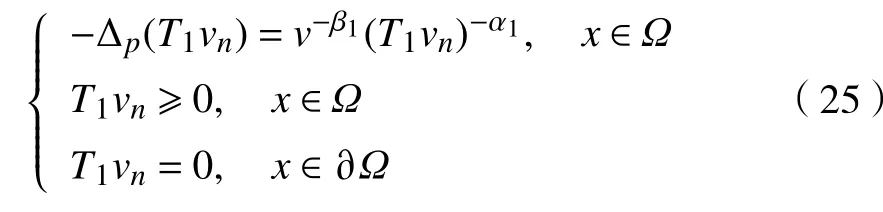
通过取极限可得

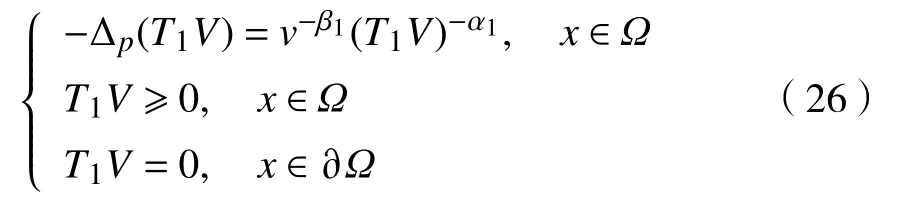
对方程

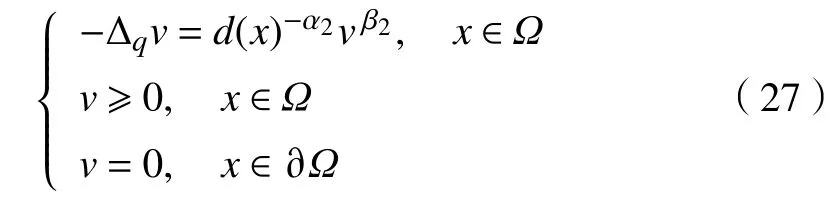
借助引理4可得式（27）的上、下解满足

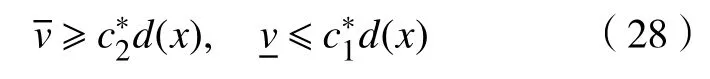
同样，对方程

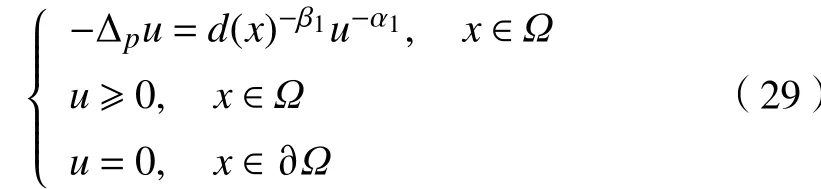
再利用引理4可以得到式（29）的上、下解满足

现选取

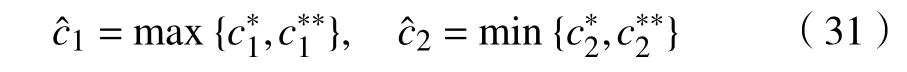
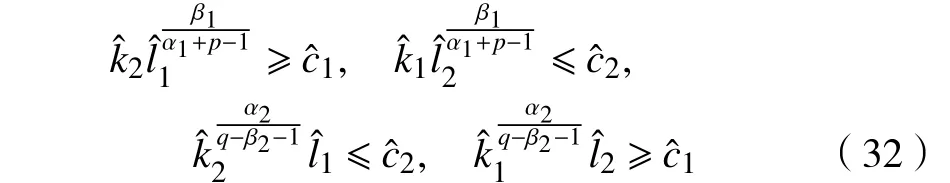
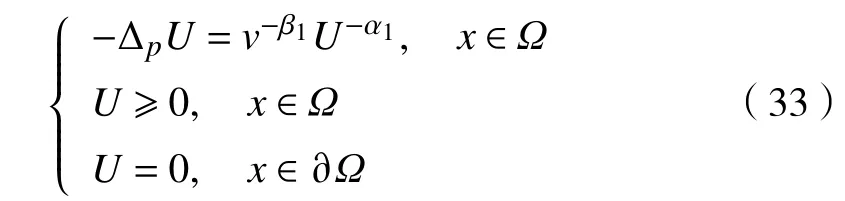
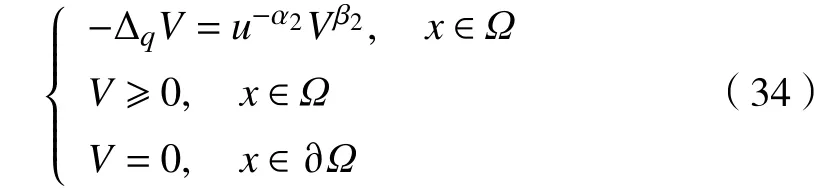
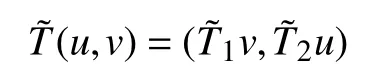
现借助Schauder不动点定理证明对于情况2方程组（2）存在正的弱解。首先要证明，然后再证明是全连续算子。