长大隧道进出口段典型沥青路面结构温度场研究

王 瑜，郭逸轩，王 睿

(1. 中交第一公路勘察设计研究院有限公司，西安 710068；2. 西安咸阳国际机场股份有限公司，咸阳 712000)

隧道内外环境因素的不同，导致洞口内外路面温度场存在差异，其中，进出口段路面温度场变化尤为复杂，在实际设计中未对其进行全面考量，极易导致该段路面过早出现病害，缩短其使用寿命，严重影响行车安全[1]。

目前，我国对公路隧道温度场的研究主要从提高围岩抗冻性的目的出发，采用实测数据拟合、理论分析法对围岩温度变化规律进行大量研究，而对寒区隧道进出口段路面温度场的研究却相对较少，部分仅进行了试探性研究。本文采用有限元法，通过研究隧道进出口段路面温度场变化特性，为青海玉树地区隧道进出口过渡段路面结构设计提供参考依据，研究结果具有重要的工程实用价值。

1 温度场计算模型及材料参数

1.1 计算模型

本文基于青海共玉公路通天河隧道工程实例，结合《公路隧道设计规范》相关规定，以设计速度v=100 km/h时的断面尺寸为标准，采用“四心圆”法及轴对称原理建立公路隧道进出口段三维模型，同时，采用可用于瞬态热分析的3D实体热单元SOLID70作为单元类型。隧道内各结构的热接触条件符合传热学中的第四类边界条件，即层间界面上的温度及热流密度是连续的[2]。三维计算模型如图1所示，具体尺寸及比例如下：

(1) 隧道径向上采用1∶1建模，初期支护厚度为18 cm，二次衬砌厚度为40 cm。

(2) 轴向采用1∶10的比例将模型纵向尺寸缩小，即有限元模型纵向长度为20 m(洞外、洞内路面实际长度均为100 m)。

(3) 确定围岩宽15 m，高20 m，路基厚度为3 m，在此围岩尺寸和路基深度条件下，有效缩短计算时间，提高工作效率。

图1 隧道进口段路面结构有限元模型

1.2 材料参数

材料的热物性决定了其热学参数随温度的变化而改变，本研究不考虑路面材料的感温性能，而将其三大热学参数视作常数。同时，围岩内部水分的存在，使围岩的感温性能更为敏感，本研究没有将水作为一种单独的材料类型，而是将其与围岩一起作为同一种材料进行考量[3]。通天河隧道进出口段铺筑路面对应的材料热学参数如表1～2所示。

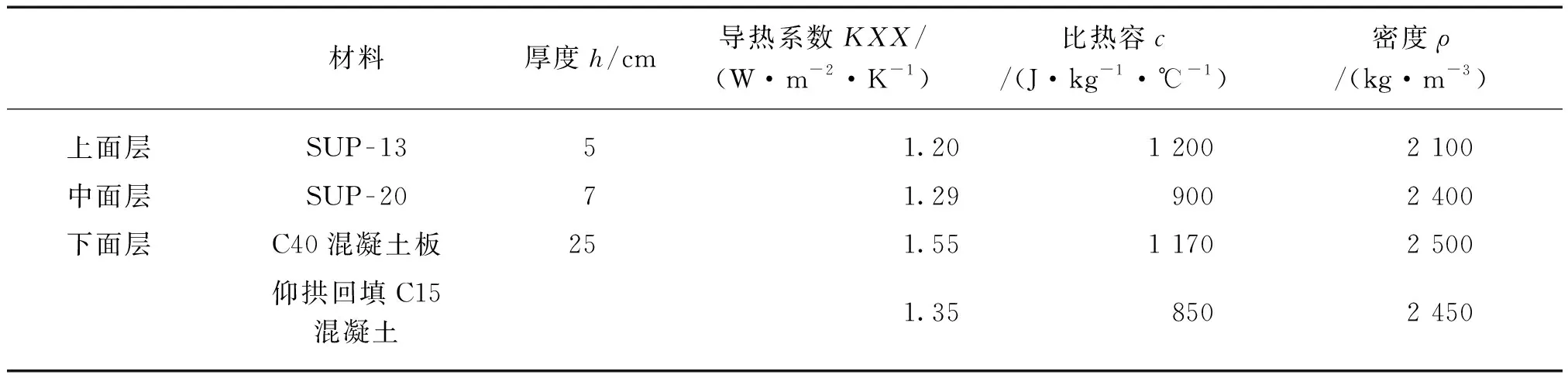
表1 隧道内复合式路面结构热学参数

表2 隧道外半刚性基层沥青路面结构热学参数

1.3 温度场边界条件

1.3.1 隧道外边界条件

根据传热学理论，本研究将隧道外界因素划分为两类边界条件，即热流密度边界条件(第二类边界条件)和对流换热边界条件(第三类边界条件)。热流密度可由路表的净辐射推算而得。

将对流换热边界条件中的空气温度和对流换热系数直接加载至路面实体单元上，热流密度加载至覆盖于路面实体单元上的SURF152表面效应单元。

(1) 热流密度边界条件

根据传热学理论及气象学理论，路表所获得的热流密度通常称之为路表净辐射值[4]，热流密度定义为单位面积截面内单位时间通过的热量(w/m2)。

路表净辐射值计算公式[5]为：

B=Q·ε·α-F

(1)

式中，B为路表净辐射值，正值为路表在热交换过程中的吸收热量，负值为路表的散失热量；Q为太阳短波辐射总量；ε为边坡系数，取为1；α为路表辐射吸收率，取0.87；F为路表有效辐射，即地面辐射与大气逆辐射的差值。

根据通天河隧道所在的玉树地区气象站提供的太阳辐射、地面辐射、大气逆辐射气象资料，由式(1)计算得出隧道洞外路表月平均净辐射值如表3所示，将其转换为热流密度如表4所示。

表3 洞外路表月平均净辐射值 (MJ·m-2)

表4 通天河隧道洞外路表热流密度 (W·m-2)

(2) 对流换热边界条件

根据传热学理论，影响该边界条件的因素主要有空气温度和对流换热系数。

① 洞外气温

根据玉树气象站提供的气象资料及洞口处实测数据，可得2017年通天河隧道洞外、洞口处的日平均气温，其年度变化趋势如图2所示。

图2 洞外、洞口平均气温年度变化曲线

采用正弦函数对洞口及洞外100 m的气温进行曲线拟合[1]，结果如下：

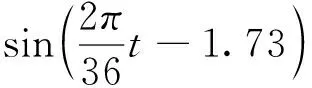
(2)

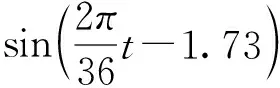
(3)

根据式(2)、(3)归纳得出隧道外空气温度沿纵向空间的年变化函数，为纵向坐标及时间的函数：

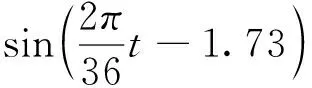
(4)

由式(4)可知，洞外100 m范围内的气温函数为高度非线性函数。

② 对流换热系数

根据Jurges-Nusselt公式计算对流换热系数[6-7]，此公式仅适用于外界风速v≤5.0 m/s的情况。

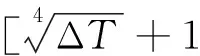
(5)

式中，ΔT为空气温度与地表温度的差值；v为空气流速(m/s)；h为对流换热系数(W/m2·K)。

结合玉树气象站提供的2017年地温及风速资料，根据式(5)计算得出洞外路表边界条件的对流换热系数，将其转换为国际制单位后如表5所示。

表5 洞外路表对流换热系数 (W·m-2·K-1)

1.3.2 隧道内边界条件

隧道内为封闭系统，其路面结构不受外界太阳辐射的影响，因此，隧道内路表温度场边界条件采用第三类边界条件，即对流换热边界条件。

(1) 洞内气温

基于通天河隧道试验路段的实测数据，采用与洞外气温相同的拟合方法，得出隧道洞口至洞内100 m的气温函数如下：

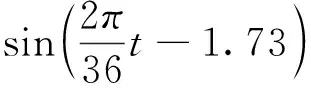
(6)

(2) 洞内对流换热系数

相关文献[1,6,8]表明，Jurges-Nusselt公式中影响对流换热系数的主要因素为外界风速，地气温差对计算结果的影响有限。实际测得洞内风速为3 m/s，计算得出洞内对流换热系数为19.82 W/m2·K。

2 路面温度场纵向变化特性

2.1 夏季阶段

隧道进出口段路面夏季最高温度纵向分布趋势如图3所示，由图可知，隧道洞外各结构层顶面的夏季最高温度均高于洞内各结构层顶面，这是由于洞外路面结构暴露于自然环境中，经受着太阳辐射，相比洞内路面结构吸收了更多的热量。

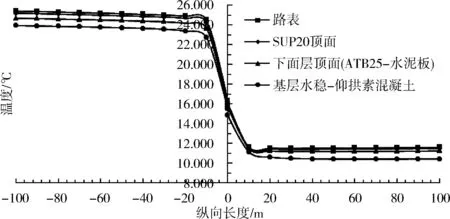
图3 进出口段路面夏季最高温度纵向分布趋势

隧道洞外20 m至洞内20 m范围内的同一结构层纵向温度差值最大，洞外及洞内20～100 m范围内各结构层顶面沿纵向最高温度分布基本趋于一条直线。洞外20 m处路表最高温度为24.9 ℃，10 m 处路表最高温度为24.5 ℃，在此纵向长度内路表最高温度呈现出小幅度的凸形趋势。路表最高温度自洞外10 m直线下降至洞内10 m，此处的路表最高温度为11.6 ℃，下降幅度达13.3 ℃，洞内10～20 m范围内路表最高温度呈现小幅凹形趋势，此后至洞内100 m处基本保持在11 ℃左右。因此，由洞内外不同自然环境导致的隧道进出口段路表最高温度纵向分布差异较大的长度范围为洞外20 m 至洞内20 m。

SUP20顶面、ATB25-水泥板顶面、基层水稳碎石-仰拱素混凝土顶面的纵向夏季最高温度分布趋势与路表状况一致，洞内外温度差异较大的纵向长度均为40 m，其洞外20 m与洞内20 m的最高温差分别为13.2 ℃、12.9 ℃、12.8 ℃，极值差随结构层深度的增加有所降低，但幅度甚小。

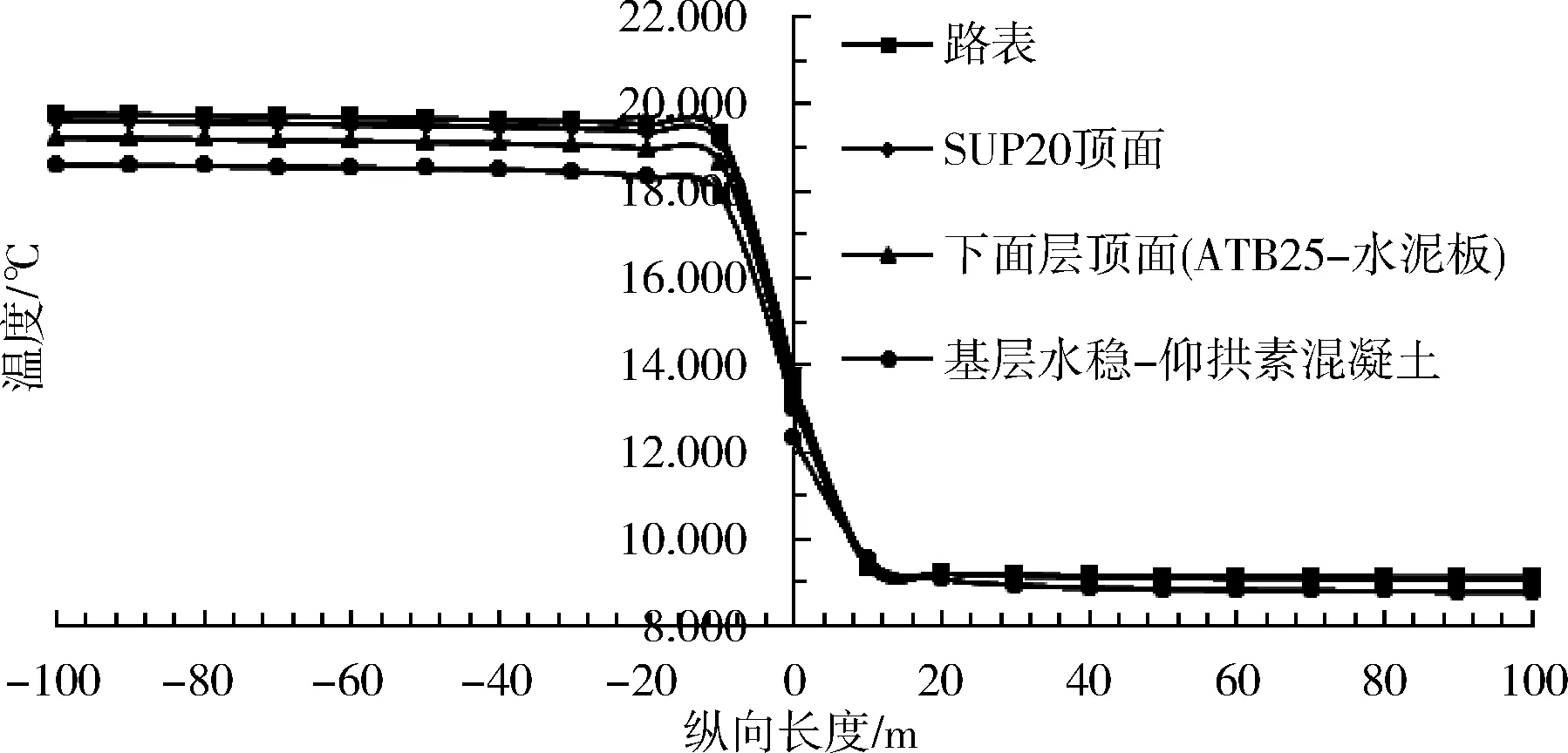
图4 进出口段路面夏季最低温度纵向分布趋势

图4为隧道进出口段路面夏季最低温度纵向分布趋势，由图可知，洞外路表的最低温度基本保持在19 ℃左右，相比最高温度降低了6 ℃，其他结构层顶面的温度极值差也基本保持在6 ℃左右；洞内路表的最低温度在9.0～9.3 ℃范围内变化，相比洞内路表最高温度降低幅度仅为2.5 ℃左右，小于洞外路表温度极值差。说明洞内路表温度在夏季阶段的变化幅度小于洞外路表，这与隧道洞内相对稳定的空气温度、风速有关。同时，洞内各结构层的最低温度纵向分布基本趋于一条直线，但洞外结构层顶面间的温差较明显，路表与下面层顶面的温差为0.4 ℃；洞内20 m处的路表最低温度为9.2 ℃，洞外20 m处的路表最低温度为19.5 ℃，温差可达10.3 ℃，此长度范围内的路表纵向最低温度分布变化最大。其他各结构层顶面的最低温度纵向分布与路表一致，仅纵向温差随着深度的增加呈现出减小的趋势。

综上所述，在夏季阶段，隧道洞外20 m至洞内20 m纵向空间内的路面温度变化较为剧烈，表现为急剧下降的趋势，且洞外温度高于洞内温度，而其他纵向空间范围内的路面结构层温度较为稳定，基本保持一条直线。

2.2 冬季阶段

隧道进出口段路面冬季最高和最低温度纵向分布趋势如图5～6所示，由图可知，其各结构层顶面的温度极值纵向分布与夏季有所差别。处于洞外的各结构层顶面温度极值自洞外100 m至洞口处逐渐上升；处于洞内的各结构层顶面温度自洞口至洞内100 m逐渐降低。

根据图5，路面结构的冬季最高温度随深度的增加而升高，路表最低，基层水稳碎石-仰拱素混凝土顶面最高。路面结构冬季最高温度峰值均出现在洞外10 m左右，路表、SUP20顶面、ATB25-水泥板顶面、基层水稳碎石-仰拱素混凝土顶面的最高温度分别为0.37 ℃、0.50 ℃、0.80 ℃、1.20 ℃。

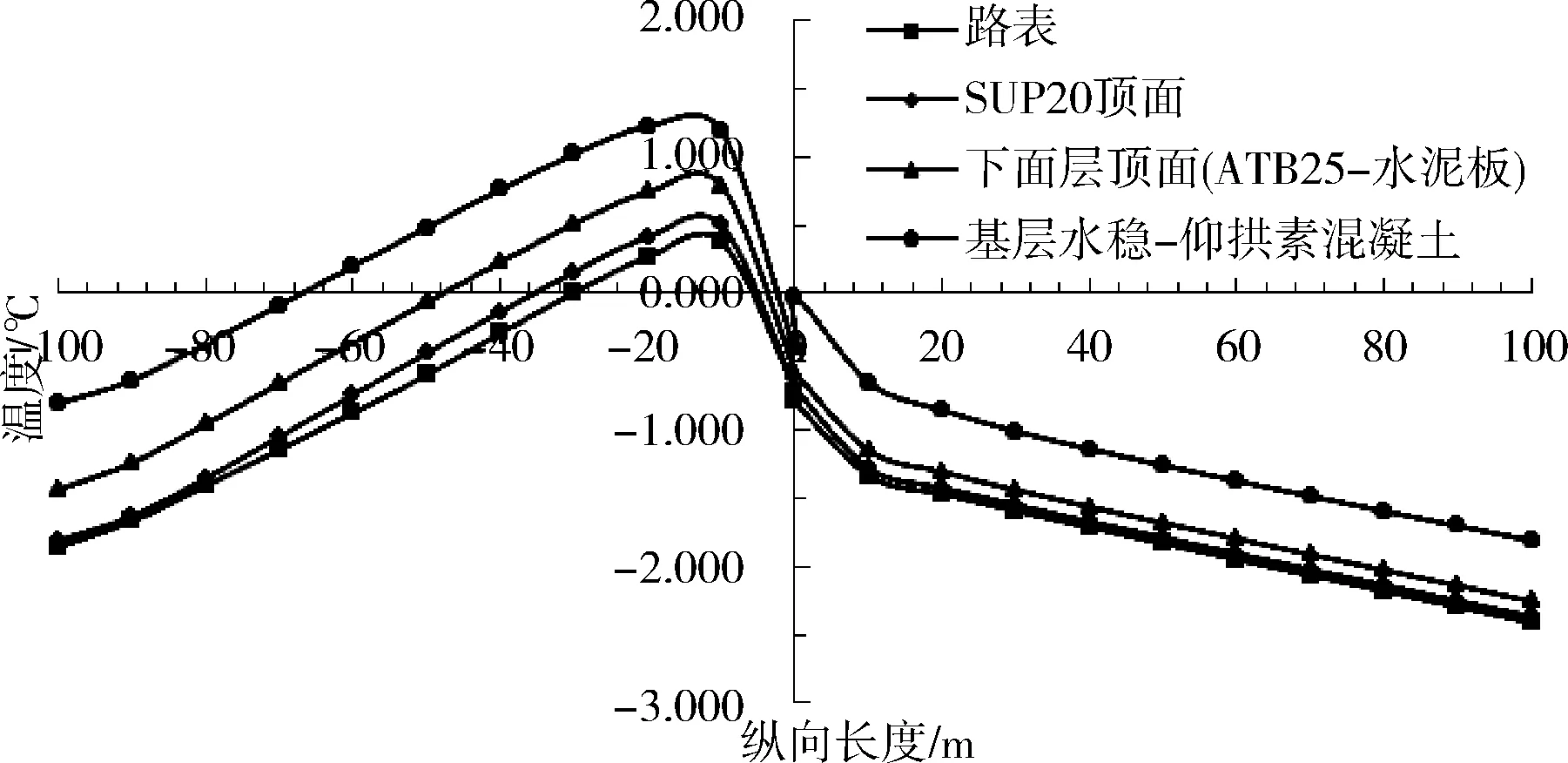
图5 进出口段路面冬季最高温度纵向分布趋势

同时，路面各结构层冬季最高温度纵向分布的正温段均处于洞外，其中路表正温段最短，为洞外30 m至洞口处，总长30 m；基层水稳碎石-仰拱素混凝土正温段最长，为洞外70 m至洞口处，总长为70 m；其他结构层正温段处于30～70 m之间。这是因为路基结构具有正积温效应，其路基底面常年保持恒定正温，使路基结构在冬季阶段能够吸收路基底面传来的热量，对路基结构起到保温的作用，而路表则直接暴露在自然环境中，受到了空气负温的影响，其负温段相比基层更长。处于洞内的路面结构温度均在负温以下，洞口至洞内100 m路面各结构层温度沿纵向逐渐减低，其中20 m范围内的下降趋势相比20～100 m段更快。

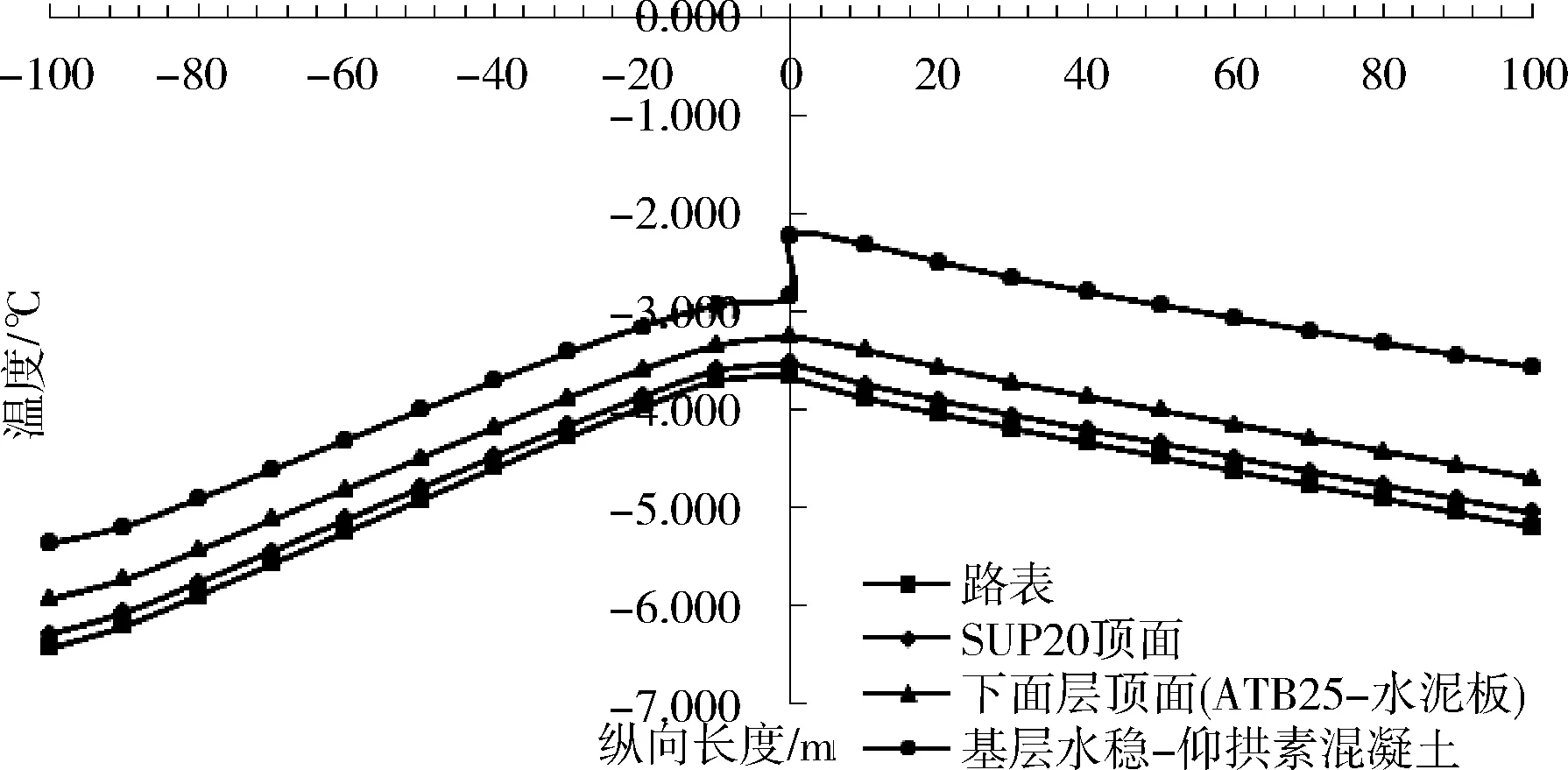
图6 进出口段路面冬季最低温度纵向分布趋势

根据图6，在冬季环境下，隧道进出口路面结构最低温度的纵向分布均为负温，且四条曲线均呈现出凸形变化规律，洞口处的结构层顶面冬季最低温度为最高值。仅有基层水稳-仰拱素混凝土顶面的温度在洞口有突变，此处的温度从-2.2 ℃降低至-2.8 ℃。其他结构层的凸形趋势较为平滑。以基层水稳碎石-仰拱素混凝土顶面的冬季最低温度纵向分布为例，可知洞外100 m至洞口范围内，其温度从-5.4 ℃平滑上升至-2.8 ℃，洞口处的顶面温度突变至-2.2 ℃，随后下降至洞内100 m处的-3.6 ℃。

3 路面温度梯度纵向变化特性

3.1 夏季阶段

隧道进出口段路面夏季最高温度梯度纵向分布趋势如图7所示，由图可知，各结构层顶面夏季最高温度梯度纵向分布在洞外20 m至洞内20 m的范围内变化较大，呈现出大幅度凸形趋势，此趋势随着结构深度的增加逐渐减弱，该纵向范围外温度梯度较为稳定，基本趋于一条直线，洞外路表温度梯度高于洞内。

图7 进出口段路面夏季最高温度梯度纵向分布趋势

洞外20～10 m范围内路表最高温度梯度上升缓慢，而10 m至洞口处急剧上升，差值可达10 ℃/m，其中洞外20 m处的路表最高温度梯度为6.7 ℃/m，洞外10 m为7.7 ℃/m，而在洞口处温度梯度剧增至18.0 ℃/m，为路表温度梯度最大值；洞内10 m处的路表最高温度梯度为1.6 ℃/m，与洞口的差值为16.4 ℃/m，其下降趋势远大于洞外10 m 的上升趋势，随后洞内路表温度梯度在洞内20 m处缓慢上升至2.6 ℃/m，此后温度梯度趋于稳定。SUP20顶面、ATB25-水泥板顶面夏季温度梯度最高值的纵向分布趋势与路表相似。

3.2 冬季阶段

隧道进出口段路面冬季最高温度梯度纵向分布趋势如图8所示，由图可知，冬季洞外路面各结构层顶面的温度梯度最高值在20～100 m范围内呈缓慢上升趋势，无突变现象；洞内各结构层顶面的温度梯度在20～100 m范围内较为稳定。其中，洞外20～10 m范围内，路表温度梯度从3.9 ℃/m下降至3.6 ℃/m，洞口处的路表温度梯度峰值相比洞外10 m处急速上升至7.1 ℃/m，洞内10 m处下降为4.5 ℃/m，在洞内20 m处路表的温度梯度为4.1 ℃/m，达到稳定值。

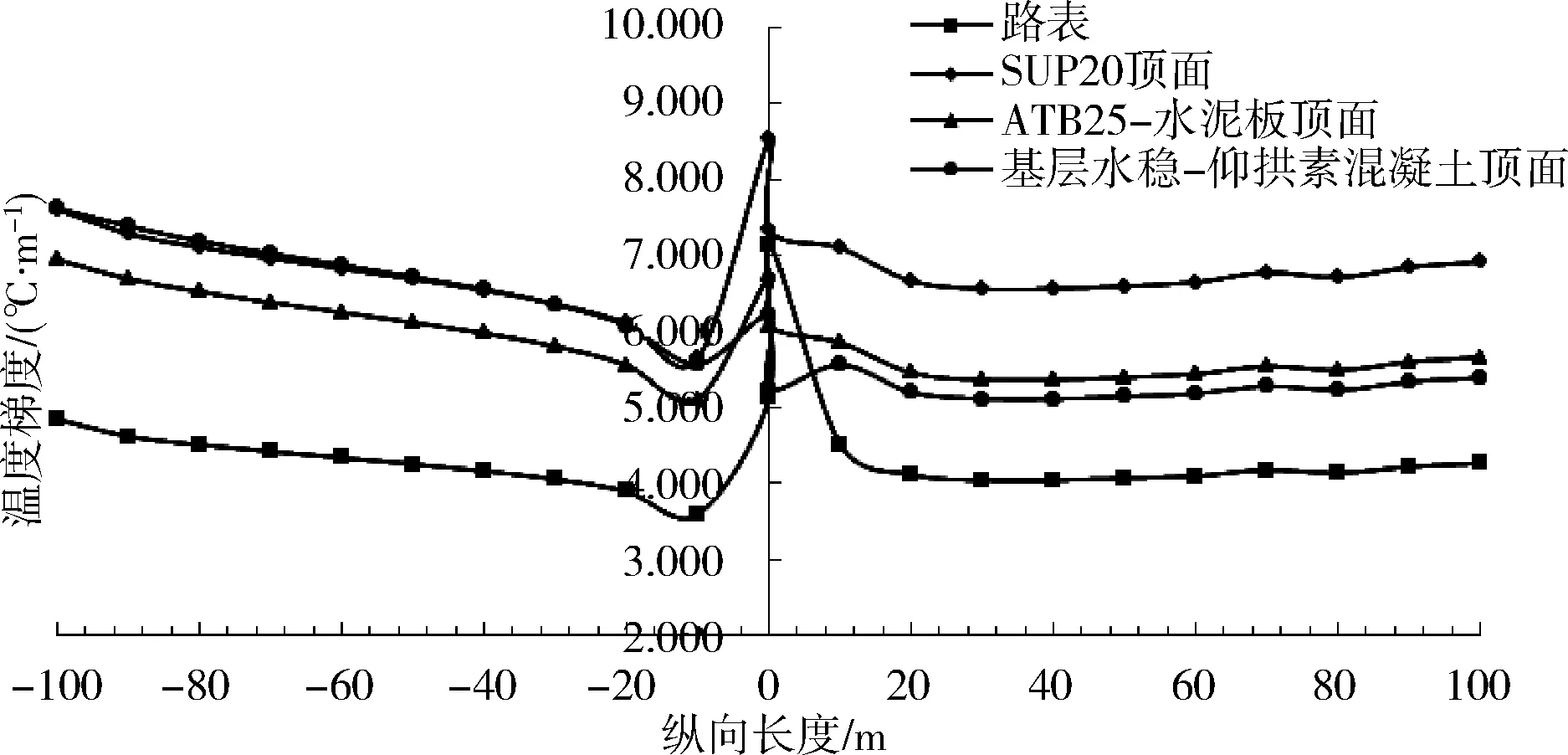
图8 进出口段路面冬季最高温度梯度纵向分布趋势

SUP20等结构层顶面的冬季温度梯度最高值纵向分布与路表一致，均在洞外20 m至洞内20 m范围内变化较大。洞口结构层顶面温度梯度峰值随着结构深度的递增而减小，其中，SUP20顶面、ATB25-水泥板顶面、基层水稳碎石-仰拱素混凝土顶面的冬季温度梯度峰值分别为7.3 ℃/m、6.1 ℃/m、5.3 ℃/m。

4 结语

(1) 本文结合青海玉树地区通天河隧道的实际工程情况及气象资料，建立了玉树地区公路隧道进出口段路面结构温度场计算模型，并确定了洞内外温度场边界条件。将洞外路面温度场归结为第二类边界条件及第三类边界条件，将洞内空气温度和风速归结为洞内路表的第三类边界条件。

(2) 在夏季阶段，隧道洞外20 m至洞内20 m纵向空间内的路面温度极值变化较为剧烈，表现为急剧下降的趋势，且洞外温度高于洞内温度。而其他纵向空间范围内的路面结构层温度较为稳定，基本保持一条直线。在冬季阶段，处于洞外的各结构层顶面温度极值自洞外100 m至洞口逐渐上升；处于洞内的各结构层顶面温度自洞口至洞内100 m逐渐降低。

(3) 隧道进出口段路面各结构层顶面夏冬两季最高温度梯度纵向分布在洞外20 m至洞内20 m的范围内变化较大，呈现凸形趋势，该纵向范围外温度梯度较为稳定，基本趋于一条直线，洞外路表温度梯度高于洞内。