卧式伺服缸新型结构控制系统的IMC-PID控制器设计

马丽楠，黄庆学，2，马强俊，张文泽，马立峰，韩贺永

(1.太原科技大学 重型机械装备协同创新中心，太原 030024；2.太原理工大学 机械工程学院，太原 030024)

由于在冶金等特殊生产线上，重载伺服缸需卧式铰接安装，旋转一定的角度输出曲线力，但由于缸筒自身重量的影响，会损坏密封结构，发生泄漏等现象，导致伺服缸输出力不足，不仅严重影响到伺服缸的使用寿命，更严重影响配套设备的生产效率[1-3]，因此，在卧式伺服液压缸端底设计了一个支撑小缸的新型结构以及配套的压力-位置双闭环独立PID控制系统。本文主要研究双闭环独立PID控制器参数整定多且复杂的问题，该控制系统需要同时整定6个参数，整定困难，易产生误差，难以实现符合工况所需的精确稳定控制。

针对PID参数整定困难问题，国内外学者取得了很多显著成就。SAMAKWONG et al[4]利用遗传算法对PID控制器的参数进行优化，来提高伺服系统的控制性能，其仿真实验证明了基于遗传算法的PID控制器具有良好的控制性能，能够提高控制系统的动态性能。SUNGTHONGA et al[5]针对热风机的温度控制，提出粒子群PID控制器设计，通过粒子群优化算法来优化PID参数，得到系统的最优性能，其仿真结果表明，经PSO优化的PID控制器相较于遗传算法、Z-N算法等有着较好的效果。TOMERA et al[6]通过将蚁群算法应用于船舶转向控制系统，对PID参数进行优化调整，其结果分析可以得到：该方法的控制效果良好，优于经典PID法、遗传算法等。

刘胜等[7]针对传统PID控制器参数整定过程繁琐问题，提出一种采用搜索者优先算法的PID自整定方法，通过将改进的PID自整定算法应用于直流调速系统，得出该优化算法的控制效果更好，适用性更强。孙航等[8]在大型光电经纬仪速度环通过利用模糊控制器对PID的比例和微分系数进行自动调整，从而实现PID参数自整定，其仿真结构表明：模糊PID具有参数自整定的能力，并且仿真结果优于传统PID.赵晓军等[9]针对利用传统的Z-N算法以及遗传算法等得到的PID参数，难以获得最优控制效果问题，提出基于果蝇优化算法的PID控制器设计，仿真结果表明：果蝇优化算法明显优于Z-N算法和遗传算法，具有收敛速度快，控制效果好等优点。

为了克服压力-位置双闭环独立PID控制系统的参数整定困难问题，本文基于上述国内外研究提出IMC-PID控制器设计。与传统PID控制器相比较，内模控制器具有结构简单，可调参数少且整定简单，鲁棒性强等优点，将内模控制与PID相结合，可以克服PID参数整定困难等较多问题，提高控制系统的动态特性，优化系统的控制性能[10-11]。

1 新型结构设计原理

针对卧式伺服缸缸筒自身重量所产生的不良影响而导致伺服缸使用寿命缩短以及降低配套设备的生产效率等问题，设计了卧式伺服缸端底连接一个支撑小缸的新型结构及其配套的压力-位置双闭环控制系统[12-13]。其原理如图1所示。

1—伺服缸；2—支撑小液压缸；3—比例换向阀；4—比例溢流阀；5—控制器；6—液压泵；7—联轴器；8—电动机；9—压力传感器；10—位移传感器图1 新型结构控制原理图Fig.1 Schematic diagram of new structure control

该控制系统是通过对小缸的压力与位移进行独立闭环控制，时刻跟踪给定信号，来平衡掉卧式伺服缸缸筒自身的重量，避免活塞杆与导向套之间的摩擦力过大，破坏密封结构，使卧式伺服缸的活塞杆全程悬浮于导向套中，近似无摩擦做功。

2 IMC-PID控制器设计

2.1 IMC-PID控制设计原理

图2所示为内模控制系统结构图，其中r(s)为系统输入，d(s)为系统扰动，y(s)为系统输出。Q(s)、G(s)、M(s)分别为内模控制器、被控对象、过程模型。

图2 内模控制系统结构图Fig.2 Internal model control system structure

通过内模控制原理分析，依据内模控制器设计过程，可知过程模型能够分解为：

M(s)=M+(s)M-(s) .

(1)

式中：M+(s)为非最小相位，不可逆部分，包含了系统的右半平面零点以及时滞环节，M-(s)为稳定的最小相位，可逆部分。

为了确保系统的稳定性和鲁棒性，需要在最小相位部分加上滤波器，为此，内模控制器Q(s)可由下式设计出：

(2)

其中，f(s)为低通滤波器。

低通滤波器通用形式为：

(3)

式中：β为滤波器参数，内模控制器中仅有的可调参数；γ为滤波器的阶次。

通过对内模PID控制器设计方法进行分析研究，可将内模控制系统结构图等效的转换为反馈控制系统结构图，如图3所示，其中Gc(s)为反馈控制器。

图3 内模控制等效反馈控制结构图Fig.3 Internal model control equivalent feedback control structure

依据内模PID控制器的设计方法，由图2所示的内模控制系统结构图可得内模控制器为：

(4)

由图3所示的反馈控制结构图可得：

(5)

2.2 双闭环控制系统的IMC-PID控制器设计

压力-位置双闭环控制系统具有一定耦合特性，通过解耦运算，分别得出[13]：

位置闭环控制系统的传递函数为：

X(s)=0.94×(1.38×10-10s5+6.49×10-8s4+
3.278 5×10-5s3+0.007 2s2+s)-1.

(6)

压力闭环控制系统的传递函数为：

(7)

由于高阶系统的控制器设计及仿真比较复杂，有时候甚至是不可实现的，因此，针对压力-位置双闭环控制系统的传递函数，运用次最优法模型降阶法进行降阶处理[14]。

降阶后的带有时间延迟的位置闭环控制系统传递函数：

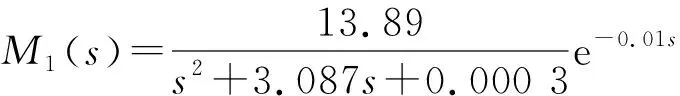
(8)

降阶后的带有时间延迟的压力闭环控制系统传递函数：

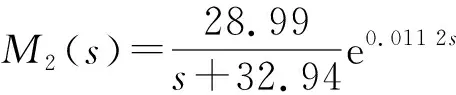
(9)

1) 针对降阶后的位置闭环控制系统传递函数进行内模PID控制器设计，则：

(10)

滤波器选取：

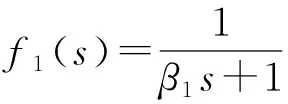
(11)

得到反馈控制器如下：

(12)

为了使反馈控制器具有PID控制器的形式，用一阶泰勒表达式逼近时滞项：

e-0.01s=1-0.01s.

(13)

则可得反馈控制器为：

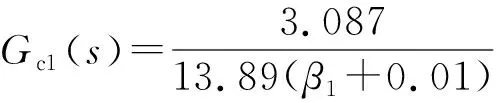
(14)

2) 针对降阶后的压力闭环控制系统传递函数进行内模PID控制器设计，则：

(15)

同样选取滤波器：

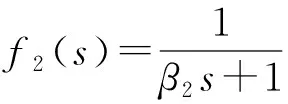
(16)

得到具有PID形式的反馈控制器如下：

(17)

3 IMC-PID控制器与PID的对比仿真

为了进一步验证内模PID在位置控制系统中应用的优良性，与PID控制器进行对比分析，如图4所示为位置控制系统的仿真对比模块。

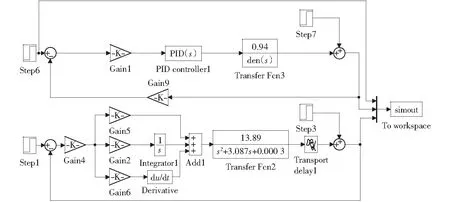
图4 位置控制系统对比仿真Fig.4 Position control system contrast simulation

其仿真结果如图5所示。

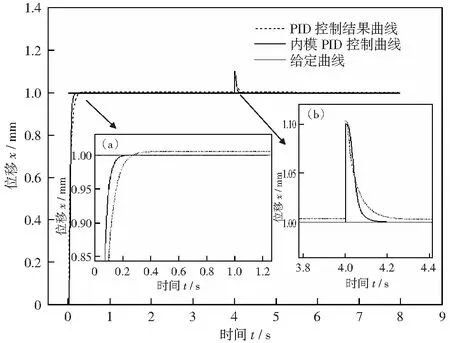
图5 位置闭环对比仿真结果Fig.5 Position closed-loop contrast simulation

由部分放大图5(a)可以看出基于内模PID控制的位置闭环相比较于PID优势更加明显，基本上在0.2 s后，位置曲线就能够稳定的达到了目标值，而PID控制的位置曲线在0.4 s后才趋于稳定，接近于目标值，但并没有精确到目标值。由部分放大图5(b)可以看出，当加入扰动后，基于内模PID控制的位置闭环能够在0.2 s的时间内快速、精确的回到目标值。而PID控制的位置曲线需要在0.3 s后才能稳定接近目标值，相比较内模PID有着明显的劣势。

为了进一步验证内模PID在压力控制系统中应用的优良性，与PID控制器进行比对分析，如图6所示为压力控制系统的仿真对比模块。其仿真结果如图7所示。

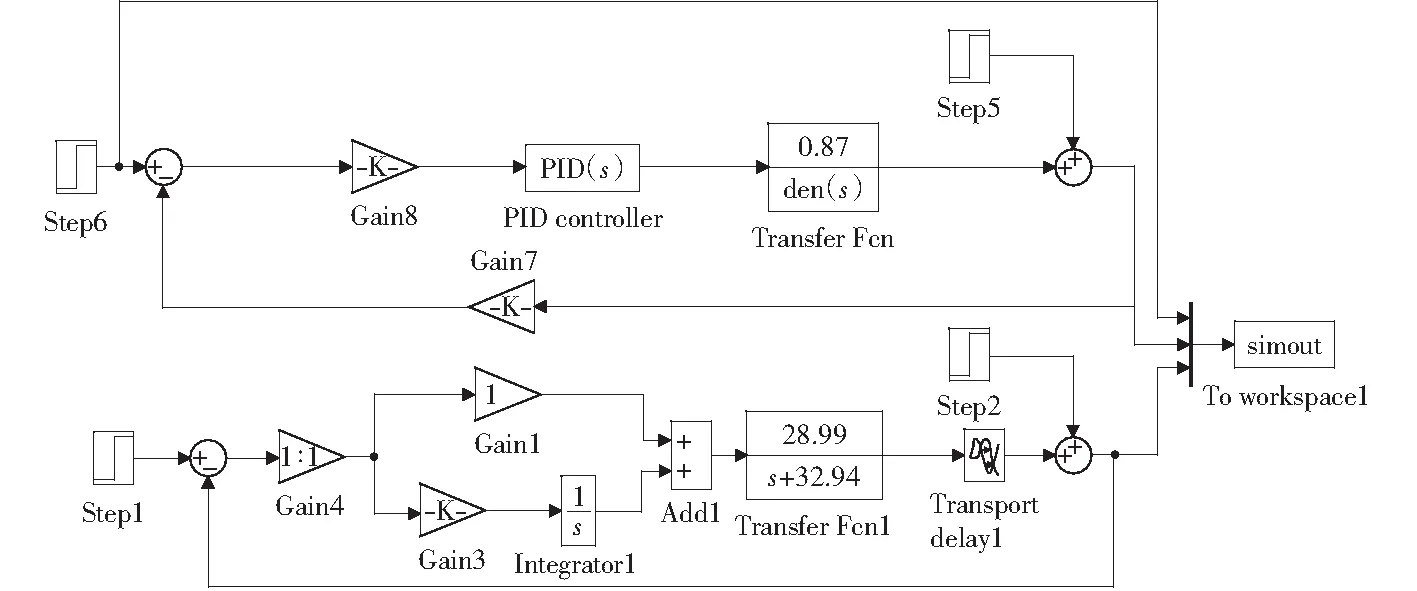
图6 压力控制系统对比仿真Fig.6 Pressure control system contrast simulation

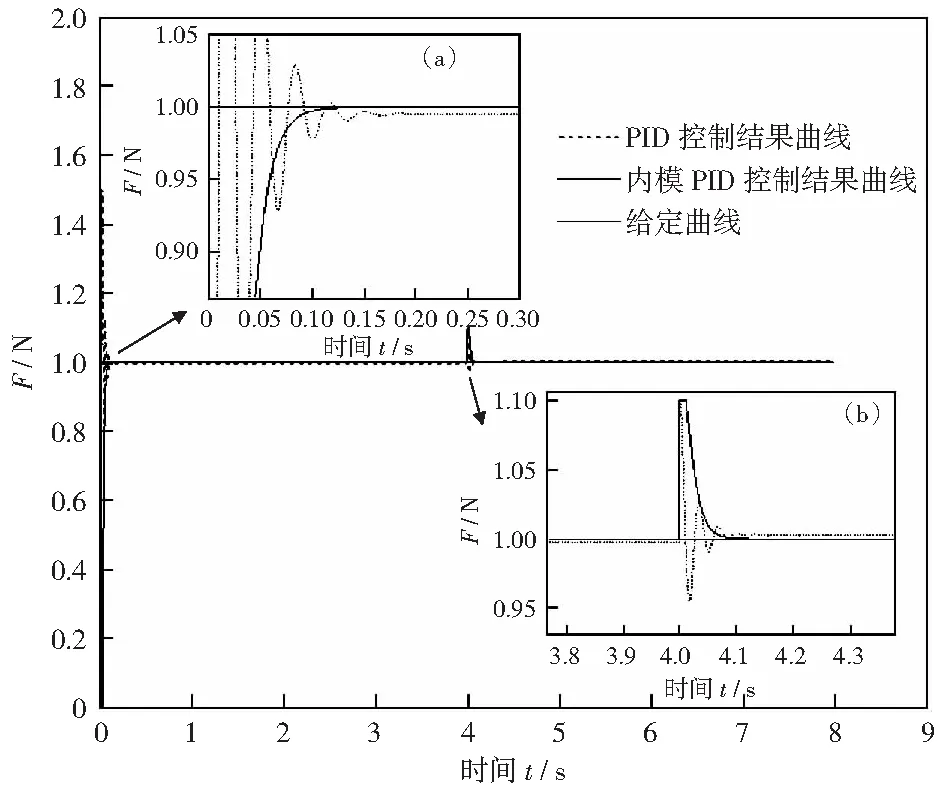
图7 压力闭环对比仿真结果Fig.7 Pressure closed-loop contrast simulation

由部分放大图7(a)可以看出内模PID的控制效果明显比PID好，内模PID控制的压力曲线在0.1 s后就达到目标值，能够保持稳定，没有振荡，而由PID控制的压力曲线在0.15 s前还有明显振荡，稳定性相对于内模PID来说较差，0.15 s后才慢慢趋于目标值，且精度明显不足，有明显的误差。根据部分放大图7(b)可以看出，基于内模PID控制的压力闭环相比较于PID来说，抑制扰动响应效果更加明显，响应时间相差0.06 s左右，且内模PID没有振荡，更加稳定，能够精确快速达到目标值。

4 结论

针对重载卧式伺服缸在工程实际中，由缸筒自身重量产生的不良影响所导致伺服缸使用寿命缩短以及配套设备生产效率降低等问题，设计了在卧式伺服缸端底连接一个支撑小缸的新型结构以及配套的压力-位置双闭环独立PID控制系统。本文通过内模控制与PID相结合的方法，提出内模PID控制器设计，克服了PID控制器参数整定困难等问题，运用Simulink仿真平台对内模PID进行了仿真研究，对比PID控制效果表明：内模PID控制器能够有效地改善系统的动态特性，并提高系统的鲁棒性，有着良好的控制效果，为实际工程提供了重要的理论依据。