有限域上低差分函数研究进展
屈龙江 陈 玺 牛泰霖 李 超
(国防科技大学文理学院 长沙 410073) (ljqu_happy@hotmail.com)
密码学是网络空间安全和信息安全的核心,作为一门综合性学科,其发展与国家安全息息相关,也与政治、军事、外交等国家事务密不可分.对称密码学是密码学的重要分支,主要研究对象包括分组密码、流密码、Hash函数等.对称密码算法是各国政府、军事和银行等重要部门保护核心敏感信息的主要算法.密码函数包含布尔函数与向量函数(S -盒)两大类,是构成序列密码、分组密码和Hash函数等对称密码算法的核心组件,而且往往是唯一的非线性组件,其密码学性质的好坏对基于该组件设计的密码算法的安全性有着至关重要的影响[1-9],相应的密码算法对于各种已知攻击的抵抗性可以由它所使用密码函数的相应密码学指标来衡量.
差分攻击是攻击迭代分组密码最有效的方法之一.差分攻击的基本思想是通过分析明文对差值对密文对差值的影响来恢复某些密钥比特.一个密码算法抵抗差分攻击的能力与其采用的密码函数抵抗差分攻击的能力密切相关,而后者可以用差分均匀度来衡量.一个密码函数的差分均匀度越小,其抵抗差分攻击的能力就越强.有限域Fq上的低差分函数主要包括完全非线性函数(perfect nonlinear func-tion, PN函数)、几乎完全非线性函数(almost perfect nonlinear function, APN函数)和差分均匀度为4的函数(4-uniform function, 4差分函数)等.当有限域的特征为奇数时,PN函数、APN函数分别达到最优、次优的差分均匀度;而在偶特征的有限域上,差分均匀度必然为偶数,此时APN函数、4差分函数分别达到最优、次优的差分均匀度.由于绝大多数密码算法用的密码函数是定义在偶特征有限域上的,所以在密码研究中,APN函数、4差分函数受到了更多关注.但是需要注意的是,PN函数、APN函数和4差分函数等低差分函数之间有着十分紧密的联系,很多构造是相互启发的.
为了抵抗差分攻击、线性攻击和插值攻击等分析方法,一个理想的S -盒通常应同时具有低差分均匀度,高非线性度和高代数次数等多种良好密码学性质.由于在代替置换网络(substitution-permutation-network, SPN)结构分组密码S -盒的设计中,为了避免熵泄露,一般要求分组密码中使用的向量函数是置换;而为了软硬件实现时具有较高的效率,又希望其定义在二元域的偶数维扩域上,因此相比一般的4差分函数,偶扩张上的4差分置换的构造与分析近年来受到了更多研究和关注.另外,由于具有对合性质的函数可以提高硬件实现的效率,这一性质在研究中也受到了较多关注.因此,本文主要总结了PN函数、APN函数和偶扩张上的4差分置换方面的研究进展.最后,需要说明的是,低差分函数在编码和通信领域中也有广泛应用,比如满足特定性质的密码函数可以用来构造性能优良的纠错码和跳频码[10],并且所构造的码参数与原有密码函数的非线性度等安全性指标密切相关.
1 基本概念和知识
1.1 基本概念
设Fq为q=pn元有限域,其中素数p为其特征,则Fq可以看作Fp上的n维向量空间.事实上,设f(x)∈Fp[x]是一个n次不可约多项式,α为其在分裂域中的一个根,则:
Fpn={a0+a1α+…+an-1αn-1|a0,a1,…,an-1∈Fp},
如果F为有限域Fpn到其自身的映射,则它可以表示为Fpn上的单变元多项式:

定义1.代数次数.设F为有限域Fpn到其自身的映射,其单变元表示为
那么F的代数次数定义为
degF=max{wp(j)|j=0,1,…,pn-1,δj≠0}.
需要指出的是,这个概念和常见的“多项式次数”的概念有所不同,比如F2n上的单项式F(x)=x3的多项式次数为3,但它的代数次数为2(因为3=2+1=(11)2).如果一个函数的代数次数不超过1,则称其为仿射函数.不含常数项的仿射函数,称为线性函数或者线性化多项式.
设F为有限域Fpn到其自身的映射.若Fpn中的每一个元素在其像集中都恰好出现一次,则称F为Fpn上的置换.若函数G满足G(F(x))=x,则称G为置换F的逆.若置换F的逆恰为其自身,即有F(F(x))=x,则称F是对合函数.

δF(a,b)=#{x∈Fq|F(x+a)-F(x)=b}.
(1)

称F的差分均匀度为ΔF或称F为ΔF-差分(一致性)函数.
一个密码函数的差分均匀度越小,其抵抗差分攻击的能力就越强.特别地,若ΔF=1,则称其为完全非线性函数(PN函数);若ΔF=2,则称其为几乎完全非线性函数(APN函数).当有限域的特征为偶数时,注意到若x0是式(1)的解,则x0+a必然也是式(1)的解,这表明式(1)的解必然成对出现,因此差分均匀度必然为偶数.这表明在偶特征的有限域上,APN函数、4差分函数分别达到最优、次优的差分均匀度.事实上,若q为偶数,则Fq上的一个函数的差分均匀度可以取从2到q的所有可能的偶数;若q为奇数,则Fq上的一个函数的差分均匀度可以取除q-1外,从1到q的其他任一整数[11].另外,需要说明的是,差分均匀度和完全非线性函数均可以推广定义到一般的交换群上,相关工作这里不再赘述,感兴趣的读者可以参阅文献[12].
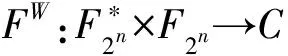
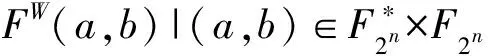

F的非线性度定义为
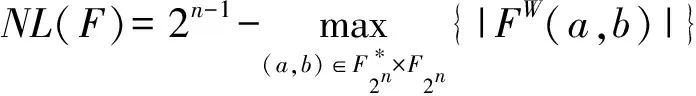
当n为奇数时,非线性度NL(F)的上界为2n-1-2(n-1)2,达到该最大值的函数称为几乎Bent函数(almost Bent function, AB函数);当n为偶数时,人们猜想非线性度NL(F)的上界为2n-1-2n2.若能达到该值,则称之为达到已知最优非线性度的函数.
1.2 CCZ等价与EA等价
新的低差分函数的构造是密码函数研究中的重要问题,它涉及到这些函数之间的等价性问题.最主要的等价性有2个:CCZ等价和EA等价.
定义4.扩展仿射等价.设F,G为2个Fq到自身的函数,若存在仿射置换函数l1,l2和仿射函数l3,使得F=l1∘G∘l2+l3,则称F和G扩展仿射等价(extended affine equivalent, EA等价).特别地,若l3=0,则称F和G仿射等价.
定义5.CCZ等价.Fq上函数F的图定义为{(x,F(x)):x∈Fq},若2个函数的图仿射等价,则称这2个函数CCZ等价(Carlet-Charpin-Zinoviev equivalent, CCZ等价).
容易验证EA等价意味着CCZ等价;但是反之不然.CCZ等价保持函数的差分均匀度和非线性度(更准确地说,是保持函数的扩展Walsh谱),而EA等价还保持代数次数(如果函数的代数次数≥2).一般而言,在理论上证明2个无限函数类是否CCZ等价是一个非常困难的问题,而判断EA等价则要简单许多.
由于在理论上分析不同函数之间的CCZ等价性非常困难,实践上人们一般通过计算机计算一些CCZ等价不变量,比如差分均匀度、扩展Walsh谱、Γ-秩、Δ-秩和各种形式的自同构群等.如果2个函数有不同的CCZ等价不变量,则它们一定不等价;反之则不能判断.另外,一个无限函数类的差分均匀度、扩展Walsh谱等CCZ等价不变量的有效计算研究在理论上和应用上都是很有意义的,特别是扩展Walsh谱的计算.这不仅是因为由扩展Walsh谱可以决定出非线性度,还因为:由APN函数可以构造性能优良的线性码,并且APN函数的扩展Walsh谱对应于该线性码的重量分布,而线性码的重量分布是线性码的一个重要参数,利用其可以有效计算译码算法的错误概率.
2 PN函数
2.1 性质与判定
PN函数有一些等价判别准则.
定理1.设F:Fpn→Fpn,则3个条件等价:
1)F为PN函数,即对任意a,b∈Fpn,a≠0,方程F(x+a)-F(x)=b至多有1个解;
2) 对任意的0≠a∈Fpn,函数DaF为Fpn上的置换多项式,其中DaF=F(x+a)-F(x);
3)D={(x,F(x))|x∈Fpn}为Fpn×Fpn中的(pn,pn,pn,1)-相对差集.
除此之外,有限域上的PN函数还可以用来构造达到Welch界的最优码本(codebook),量子测量、量子计算中有重要作用的最优互无偏基(mutually unbiased base,MUB)以及压缩感知中的最优相干矩阵(coherence matrix)等.由于本文主要是从密码学的角度论述,这些联系就不再赘述了,感兴趣的读者可以参阅文献[13-15].
特别地,对于二次PN函数,也称为Demobowski-Ostrom(DO)型函数,有等价判定准则:
定理2.设F:Fpn→Fpn且为二次函数,则2个条件等价:
1)F为PN函数,即对任意0≠a∈Fpn,函数DaF=F(x+a)-F(x)为Fpn上的线性化置换多项式;
2) (Fpn,+,*)为有限交换预半域,其中“*”为Fpn上定义的乘法:
x*y=(F(x+y)-F(x)-F(y))2.
预半域与域相比,可能失去结合律且可能不含单位元.
2008年Kyureghyan和Pott证明了2个PN函数CCZ等价当且仅当它们EA等价[16].因此相比于一般函数的CCZ等价性判断,PN函数CCZ等价性判断的难度略小一些,但仍很困难.
2012年翁国标和曾祥勇刻画了DO型PN函数的映射性质[17].
定理3[17].设F为Fpn[x]中的DO型多项式,则F为PN函数当且仅当其像集中的每一个非零元均有2个原像,即F是2到1的映射.
2.2 已有构造
2005年以前,有限域Fpn上PN函数的研究主要集中于幂函数(单项式),包括2类(不等价的)PN幂函数:
1) Demobowski-Ostrom幂函数[18]:
π1(x)=xpt+1,
其中,整数t≥0,ngcd(n,t)为奇数;
2) Coulter-Mattews幂函数[19]:
其中,整数p=3,k为奇数且n和k的最大公约数gcd(n,k)=1;
2006年以后,人们陆续发现了一些多项式形式的二次PN函数.目前Fpn上已知的多项式PN函数有:
1) Ding-Yuan多项式[19-20]:
π3(x)=x10-μx6-μ2x2,

2) Zha-Kyureghyan-Wang多项式[21]:
π4(x)=xps+1-μpkxplk+p-lk+s,
其中,整数n=3k,(3,k)=1,kgcd(k,s)为奇数,s≡±kmod 3且μ为中本原元;
3) Budaghyan-Helleseth第1类多项式[22]:
4) Budaghyan-Helleseth第2类多项式[22]:
π6(x)=bxps+1+(bxps+1)pk+cxpk+1+
5) Bierbrauer多项式[23]:
π7(x)=xpt+1-αxp2s+ps+t,
其中,n=3s,q=ps,q′=pt,s′=sgcd(s,t),t′=tgcd(s,t),s′为奇数,a∈Fq3且其阶为q2+q+1,s+s′≡0 mod 3或q≡q′ mod 3.
如定理2所述,上述二次PN函数还等价于交换预半域.人们还构造了一些其他的半域,其对应的多项式较复杂,下面列出这些半域,感兴趣的读者可以自行推导其对应PN函数的多项式表达式:
1) Dickson半域[24]:定义在Fq2k上,其乘法定义为
(a,b)*(c,d)=(ac+αbqdq,ad+bc),
其中,α∈Fqk为一个非平方元;
2) Ganley半域[25]:定义在F32k上,其中k≥3为奇数,其乘法定义为
(a,b)*(c,d)=(ac-b9d-bd9,ad+bc+b3d3)
3) Cohen-Ganley半域[26]:定义在F3n上,其中n≥2,其乘法定义为
(a,b)*(c,d)=(ac+βbd+β3(bd)9,
ad+bc+β(bd)3),
其中,β∈F3n为一个非平方元;
4) Zhou-Pott半域[27]:设n=2m,k为正整数,且mgcd(m,k)为奇数,定义x∘ky=xpky+ypkx,设(a,b)*(c,d)∈Fp2m,乘法定义为
(a,b)*(c,d)=(a∘kc+α(b∘kd)δ,ad+bc)
其中,α∈Fpm为一个非平方元;δ为Fpm上的一个自同构.
除此之外,人们还在F35,F38,F55中发现了一些零散半域[28-30].目前还不能把它们推广到无限类.
从上面论述可以看出,除了Coulter-Mattews函数外,其他所有已知PN函数都是二次的,因此都对应于交换(预)半域.二次PN函数的CCZ等价性与其对应半域的同痕(isotopy)是一致的.半域同痕的不变量包括核(nucleus)、中心(center)、对应平面的自同构群等.关于上述半域同痕性的讨论,请参阅文献[31]及其引用的参考文献.
定义6.非凡完全非线性函数(exceptional perfect nonlinear function).设F:Fq→Fq, 若F在Fq的无穷多个扩域上为完全非线性函数,则称F为非凡完全非线性函数.若F(x)=xd,则称d为非凡完全非线性指数.
利用代数几何的方法,2015年Zieve[32]证明了:
定理4.设p为奇素数,d为正整数,单项式F(x)=xd为Fpn上的完全非线性函数对无穷多个整数n成立当且仅当d为下列情形之一:
1)d=pi+pj,i≥j≥0;
2)d=(3i+3j)2,p=3,i≥j≥0且i-j为奇数.
除了上述2个非凡完全非线性函数外,容易看出Ding-Yuan多项式π3(x)=x10-μx6-μ2x2也是一个非凡完全非线性函数.
本节的最后,介绍一下偶特征上的平面函数,也称为伪平面函数(pseudo-planar function)或修改的平面函数(modified planar function).PN函数仅在奇特征有限域上存在,APN函数在某种意义上可以视为PN函数在偶特征有限域上的推广,但APN函数与射影平面、码本等并没有联系.2013年周悦引入伪平面函数[33]的定义:
定义7.伪平面函数.设F:F2n→F2n,若对任意0≠a∈F2n,函数
DaF=F(x+a)+F(x)+ax
均为F2n上的线性化置换多项式,则称F为伪平面函数.
与PN函数类似,伪平面函数与射影平面、交换半域等数学对象有着深刻的内在联系,在压缩感知矩阵设计、最优码本设计等领域中有着丰富的应用.目前所有已知伪平面函数都是二次函数,都对应着F2n上的交换半域.周悦在文献[33]中给出了2类伪平面函数,分别对应着有限域和Kantor半域.随后Schmidt、周悦[34]和Scherr,Zieve[35]研究了单项式伪平面函数,给出了三类构造.2015胡思煌等人[36]构造了三类二项式伪平面函数.2016年屈龙江[37]将一大类二次函数为伪平面函数的判定问题转化为一个对应含参Dickson行列式是否非零的判定问题,大大降低了判定时间复杂度;利用该Dickson行列式系数的特殊性质能够进一步简化计算证明.该方法不仅构造了5类新的多项式伪平面函数,而且将所有已知函数都统一归纳到了一个大类中.
3 APN函数
由于密码学应用主要使用(向量)布尔函数,所以本节主要讨论偶特征域上的APN函数.对于奇特征域上APN函数感兴趣的,请参阅文献[38-40].
3.1 性质与判定
APN函数有一些等价判别准则:
定理5.设F:F2n→F2n,则6个条件等价:
1)F为APN函数,即对任意a,b∈F2n,a≠0,方程F(x+a)+F(x)=b至多有2个解;
2) 对任意使得x+y+z+t=0的两两互异的x,y,z,t∈F2n,有F(x)+F(y)+F(z)+F(t)≠0;
3) 对任意非零a∈F2n,均有|Da(F)|=2n-1,其中Da(F)={F(x+a)+F(x)|x∈F2n};
4)wt(γF)=22n-1-2n-1,其中γF为由F定义的2n元布尔函数:γF(a,b)=1当且仅当a≠0,且方程F(x+a)+F(x)=b有解[10];
5) 对任意非零a∈F2n,均有:
其中,fλ表示F的组件函数,FW(g)表示布尔函数g在x=0处的Walsh谱[41];
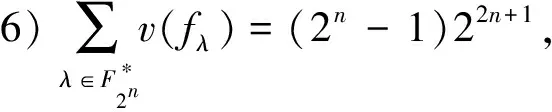
2017年Carlet以Walsh变换为工具刻画向量函数的差分均匀度,特别地,给出APN函数的如下等价判别准则:
定理6[42].设F:F2n→F2n,则F为APN函数当且仅当下列任一条件成立:
APN函数和AB函数具有联系:
定理7[10,43].设F:F2n→F2n.若F为AB函数,则F为APN函数.反过来,当n为奇数时,如果F为APN函数,且其所有Walsh谱值均被2n+1整除,那么F为AB函数;特别地,二次APN函数必为AB函数.
对于APN幂函数,Berger等完全刻画了它的映射性质.
定理8[42].设xd为F2n上的APN函数,则:
上述结果表明,F2n(n奇)上的APN幂函数必然是置换,但F2n(n偶)上的APN幂函数则不可能为置换.
2011年Leander和Rodier[44]研究了APN函数的代数次数上界,证明了x-1+g(x),其中g为非仿射函数,至多对有限个n能在F2n上为APN函数.最近Budaghyan等人[45]研究了F2n上代数次数为n的APN函数的存在性,利用差分、Walsh谱的幂级数刻画了这些函数,给出了一些不存在性的结果.特别地,证明了对于F2n上多数已知APN函数F(x),x2n-1+F(x)不是APN函数;这意味着,如果改变这些APN函数的一个点,得到的是非APN函数.
2016年Gorodilova[46]刻画了APN函数的子函数,证明了一个n元向量函数为APN函数当且仅当其2个n-1元子函数或者为APN函数,或者为4差分函数,且满足相容性条件.
3.2 已有构造
2005年以前,有限域F2n上APN函数的研究主要集中于幂函数,包括Gold函数、Kasami函数、Welch函数、Niho函数、逆函数和Dobbertin函数这6类APN幂函数.


3) Welch函数[50]:x2k+3,其中n=2k+1;
4) Niho函数[51]:x2k+2k2-1,当k是偶数时;x2k+2(3k+1)2-1,当k是奇数时;其中n=2k+1;
5) Inverse函数[52,48]:x22k-1,其中n=2k+1;
6) Dobbertin函数[53]:x24k+23k+22k+2k-1,其中n=5k.
2006年Dillon在F26上发现了很多不等价于幂函数的多项式APN函数[54].学者们从这些例子出发,陆续构造了一些与幂函数不等价的多项式二次APN函数无限类,它们的形式是通过对不同参数的Gold函数进行组合得到新的APN函数.我们将这些函数归纳总结,它们均是定义在F2n上的:
1) Budaghyan-Carlet-Leander函数[55]:
x2s+1+α2t-1x2it+2rt+s,
其中,n=lt≥12,l∈{3,4},gcd(t,l)=gcd(s,lt)=1,i≡stmodl,r=l-i,α∈F2n为本原元.
2) Bracken-Byrne-Markin-McGuire第1类函数[56]:
其中,n=2m,m为奇数,γi∈F2m,gcd(s,m)=1,s为奇数,α,β∈F2n为本原元;
3) Bracken-Byret-Markin-McGuire第2类函数[57]:
α2tx2n-t+2t+s+αx2s+1+βx2n-t+1+γα2t+1x2t+s+2s,
其中,n=3t,gcd(s,3t)=gcd(3,t)=1,3|t+s,α∈F2n为本原元,β,γ∈F2t,βγ≠1;
4) Budaghyan-Carlet第1类函数[55]:
x22s+2s+αx2m+1+βx22s+m+2s+m,
其中,n=2m,gcd(i,m)=1,α,β∈F2n使得:
β2m+1=1,β∉{λ(2i+1)(2m-1),λ∈F2n},βα2m+α≠0;
5) Budaghyan-Carlet第2类函数[55]:
x(x2i+x2m+αx2m+i)+x2i(α2mx2m+βx2m+i)+x2m(2i+1)
其中,n=2m,gcd(i,n)=1,β∈F2nF2m,并且x2i+1+αx2i+α2mx+1在F2n上没有满足x2m+1=1的解.
2009年,Budaghyan等人[58]从x3出发,构造了一类形式非常简单的在任何F2n上都存在的APN函数无限类:
并在文献[59]中构造了更多具有这种形式的APN函数无限类.Edel和Pott[60]研究了构造该APN函数的方法并提出“交换构造(switching construction)”技术,通过变换已有APN函数的坐标函数来构造新的APN函数,得到了目前唯一的一个既CCZ不等价于幂函数也CCZ不等价于二次函数的F26上的APN函数:
其中,本原元α为x6+x4+x3+x+1的一个根.
2011年Carlet[61]以及2013年周悦和Pott等人[27]分别利用向量Bent函数构造APN函数,该方法得到的构造涵盖了以往的许多构造.这2个构造都使用了双变元表示,即当n=2m时,将F2n视为F2m×F2m.
1) Carlet函数[61]:令n=2m,整数i,j满足gcd(n2,i-j)=1.令
g(x,y)=αx2i+2j+γx2iy2j+δx2jy2i+βy2i+2j,
则:
F(x,y)=(xy,g(x,y))
是APN函数当且仅当多项式
g(x,1)=αx2i+2j+γx2i+δx2j+β
在F2m中无根;

g(x,y)=x2k+1+α(σ(y))2k+1,
则:
F(x,y)=(xy,g(x,y))
是APN函数当且仅当α不能写成
a2k+1(t2k+t)(σ(t2k+t))
的形式,其中a,t∈F2m.
2014年,余玉银等人[62]提出了一个通过齐二次函数对应矩阵坐标变换的方法构造二次APN函数,在F27,F28上分别发现了471类和2252类CCZ不等价的二次APN函数.同时,翁国标等人[63]受DO函数与半域的对应启发,提出了APN代数(APN algebra)的概念来刻画二次APN函数,同样在F27,F28上发现了大量新的二次APN函数.2014年,Carlet等人[64]通过寻找特殊形式的二次置换多项式的方法在F28上找到了18类APN函数.
介绍一下非凡几乎完全非线性函数(exceptional almost perfect nonlinear function)即在无穷多个扩域上具有几乎完全非线性的函数.利用代数几何的方法,2011年Hernando和McGuire[65]证明了结果:
定理9.设d为正整数,单项式F(x)=xd为F2n上的APN函数对无穷多个整数n成立当且仅当d为Gold指数或者Kasami指数,即d=2i+1或d=22i-2i+1.
目前人们仅知道上述2个非凡APN函数.
3.3 等价性
理论上分析APN函数之间的CCZ等价性非常困难,人们一般通过计算机在小域上计算一些CCZ等价不变量来说明APN函数之间的CCZ等价性.目前APN函数CCZ等价性的理论研究主要集中于幂函数之间以及多项式函数与部分幂函数之间.虽然学者们普遍认为3.2节中所列出的APN幂函数相互之间应该是CCZ不等价的,但在很长一段时间里,Gold函数、Kasami函数、Welch函数和Niho函数四者之间的等价性以及逆函数和Dobbertin函数两者之间的等价性目前都没能给出严格的数学证明[31].直到2018年,Dempwolf[66]完全解决了幂函数之间的CCZ等价性问题.但各类多项式APN函数无限类之间的CCZ等价性依旧是公开问题.目前已有的结果可以归结为6个方面:
1) 参数不同的Gold函数之间是CCZ不等价的[67];
2) 逆函数和Dobbertin函数这2类函数与Gold函数,Kasami函数,Welch函数 和 Niho函数这四类函数之间CCZ不等价[68-69];
3) Budaghyan[55]证明了当n≥12时,论文中构造的APN函数CCZ不等价于Gold函数、Kasami函数、逆函数和Dobbertin函数且EA不等价于任何幂函数;
4) 2012年Yoshiara[70]证明了Edel的猜想:2个二次APN函数CCZ等价当且仅当它们EA等价;
5) 2017年Yoshiara[71]证明了n为偶数时,如果有2个plateaued APN函数且其中一个为幂函数,则它们CCZ等价当且仅当它们EA等价;
6) Dempwolf[66]证明了Fpn上的2个幂函数xk和xl是CCZ等价的当且仅当存在整数0≤a 另外,目前所有二次APN函数族的Walsh谱都得到了计算,结果表明,这些函数都具有与Gold函数相同的Walsh谱,即当n为奇数时为三谱值,而当n为偶数时为五谱值[72-73,58]. 为了避免熵泄露,一般要求分组密码中使用的向量函数是个置换;同时为了软硬件实现时具有较高的效率,又希望其定义在二元域的偶数维扩域(偶数维扩张,以下简称偶扩张)上.于是寻找偶扩张上的APN置换就成为了密码学研究中的一个重要问题,该问题被称为“大APN问题(big APN problem)”. 问题1.大APN问题.当n为偶数时,是否存在F2n上的APN置换? 该问题已经公开近30年了,是目前密码函数领域里最著名的公开问题.很长一段时间里,人们只能得到关于该问题的一些负面结果,于是很多密码学家和数学家猜想,F2的偶次扩域上不存在APN置换.但2009年Dillon等人发现了F26上的一个APN置换[74],然而n≥8情况下的“大APN问题”目前仍然是公开的.关于“大APN问题”,目前已知有4个方面结果: 1) 2009年Dillon通过分解一个APN函数所对应的线性码,找到了F26上的一个APN置换[74].但其表达形式非常复杂.2016年,Perrin等人[75]提出了“蝴蝶结构(butterfly structure)”,很好地从理论上诠释了这个APN置换,但是,他们的方法并没有发现偶扩张上的其他APN置换. 2)F22和F24上不存在APN置换.Langevin等人[76]结合计算机验证指出,F26上的3次APN置换一定与Dillon等人发现的APN置换是CCZ等价的. 3) 定理8表明偶扩张上的幂函数不可能为APN置换.Seberry等人证明了偶扩张上的二次函数也不可能为APN置换.Pasalic[77]、李永强等人[78-79]分别证明了某些形如一个幂函数和一个线性函数的和函数不可能为APN置换. APN函数研究的困难性有3个方面:1)一个随机函数是APN函数的概率很低,这为其搜索、构造带来很大困难;2)缺乏判断CCZ等价的有效工具,研究中人们经常会发现找到的函数CCZ等价于已知函数;3)除了单项式(幂函数)和二项式外,已知APN函数的表达形式往往比较复杂,例如Dillon等人构造的APN置换,这也进一步研究带来较大困难.因此我们对于APN函数的认识还不够深刻,亟需更深刻、更有力的研究工具. 4差分函数是偶特征有限域上具有次优差分均匀度的函数.4差分函数的构造并不困难,一种自然的方法是复合一个APN函数和一个2到1的线性函数.从密码应用角度看,由于缺乏偶扩张上的APN置换,密码算法S -盒设计的一个自然选择就是使用4差分置换,比如著名AES(advanced encryption standard)算法的S -盒使用了F28上的逆函数就是一个4差分置换.偶扩张上4差分置换的构造与性质对于对称密码设计与分析具有十分重要的意义.因此接下来本节只论述偶扩张上4差分置换. 近年来偶扩张上4差分置换的研究受到较多关注,人们给出了一系列新的构造,下面分为具有五谱值的4差分置换和从逆函数出发构造的4差分置换两大类进行叙述. 4.1.1 具有五谱值的4差分置换 已有具有五谱值的4差分置换其Walsh谱取值均为{0,±2n/2,±2(n+2)/2},因此非线性度达到已知最优2n-1-2n/2,其中一些构造的代数次数也不太低,但目前已有的构造均无法达到最优代数次数n-1. 1) 基础构造 2011年以前,偶扩张上的4差分置换无限类只有Gold函数、Kasami函数、逆函数、Bracken-Leander函数和Bracken-Tan-Tan函数5类基础构造.其中除了逆函数外,其余4类Walsh谱取值均为{0,±2n2,±2(n+2)2}. ① Gold函数[47]:x2i+1,其中n=2k,k为奇数且gcd(i,n)=2; ② Kasami函数[81-82]:x22i-2i+1,其中n=2k,k为奇数且gcd(i,n)=2; ③ 逆函数:x-1,其中定义0-1=0; ④ Bracken-Leander函数[83]:x22k+2k+1,其中n=4k,k为奇数; ⑤ Bracken-Tan-Tan函数[84]:αx2s+1+α2kx2-k+2k+s,其中n=3k,k是偶数,但3⫮k且k2是奇数,gcd(i,n)=2,3|(k+s),α是F2n上的本原元. 其中,前4类为幂函数,最后一类为二项式函数.除了Kasami函数和逆函数之外,其他函数的代数次数都是2或者3,且仅有逆函数是对合函数.容易看出,这里除了Bracken-Leander函数以外,其余3类都是从APN函数修改构造的. 2) Gold函数收缩构造 2011年Carlet提出了一种利用F22k+1上APN置换来构造F22k上4差分置换的方法[85].李永强等人对该方法进行了进一步研究,从Gold函数出发,成功地构造了2类偶扩张上的具有已知最优非线性度的4差分置换[86].其具体形式如下: 限制在T(0)上的函数. 这2类函数的代数次数为(n+2)2,但均不是对合函数. 3) 蝴蝶结构 ① Perrin-Udovenko-Biryukov构造[75]: R(x,y)=(x+αy)3+y3, ② Canteaut-Duval-Perrin构造[87]: R(x,y)=(x+αy)3+βy3, ③ Fu-Feng构造[88-89]: R(x,y)=(x+αy)2t(2i+1)+y2t(2i+1), 这些4差分置换具有已知最优的非线性度,代数次数为n2或者(n+2)2,这些函数的“开蝴蝶结构”形式均为对合的.利用“蝴蝶结构”可以给出Dillon等构造APN置换的简洁表达形式.但遗憾的是Canteaut等证明在该结构构造的函数中,除了Dillon等构造的APN置换外,没有其他APN置换. 4.1.2 从逆函数出发构造的4差分置换 当n为偶数时,逆函数x-1是对合的4差分置换[48,52],具有最优代数次数n-1,其非线性度达到已知最优2n-1-2n2,Walsh谱可以取遍±2(n+2)2之间的每一个被4整除的整数值.AES,Camellia等很多标准算法均使用逆函数做S盒.从逆函数出发构造的4差分置换普遍具有最优代数次数n-1和较高的非线性度,其中一些子类还可以达到已知最优非线性度. 1) 逆函数交换构造 2013年屈龙江等人通过“交换构造(switching construction)” 的技术研究了逆函数,提出了优先函数的概念,并且以此为工具构造为 其中,d=2n-2 或者 3(2t+1),2≤t≤n2-1的2个简洁的4差分置换无限类[90].他们又提出优先布尔函数的概念,在偶扩张上构造出了至少2(2n+2)3个形如x-1+f(x-1)的具有最优代数次数的4差分置换,从而在理论上首次证明了F22k上4差分置换的个数是随着变元个数增长而呈双指数增长的[91].这些函数都可以看作是在逆函数基础上添加某个布尔函数得到的,我们简称为BI函数,这类函数是4差分置换的充分必要条件如下[92]: BI 4差分置换:令n为偶数,ω是F2n中阶为3的元素,f是n元布尔函数.则BI函数是4差分置换当且仅当对于任意x∈F2n均有f(x)=f(x+1)且对于任意z∈F2nF4,2个等式中至少有一个成立: 查正邦等学者[93-94]、彭杰等学者[95]也先后研究了逆函数的交换构造法,并进一步研究了其中一些具有良好密码学性质的子类.BI 4差分置换具有最优代数次数和较高的非线性度,其中一些子类还具有已知最优非线性度.BI 4差分置换是对合函数当且仅当2种情况之一成立[96]: ①n=2k,k为奇数, Supp(f)={0,1},{ω,ω2}或{0,1,ω,ω2}; ②n=2k,k为偶数, Supp(f)={0,1,ω,ω2}. 2) 逆函数其他修改构造 李永强、查正邦、彭杰、唐灯和Carlet等学者也先后通过不同的方法对F2n上的逆函数进行修改,得到了一些新的4差分置换,这些4差分置换普遍具有最优代数次数和较高的非线性度.具体修改方式为: ① Li-Wang-Yu构造[97]: 其中,{ai|0≤i≤m}为满足一定条件的圈. ② Zha-Hu-Sun构造[93]: 其中,d是偶数,d|n且nd为奇数, ③ Peng-Tan构造[98]: 其中,α,β∈F2d满足某些具体条件. ④ Peng-Tan-Wang第1类构造[99]: 其中,γ∈F2n,U是循环群γ中一些集合的并. ⑤ Peng-Tan-Wang第2类构造[100]: 其中,U是F2nF4中一些六元集合的并. ⑥ Tang-Carlet-Tang构造[101]: 其中,第⑥类函数的逆变换是BI 4差分置换,因此它们是CCZ等价的.前5类函数均包含一些对合的4差分置换子类,这里不具体列出相关条件,感兴趣的读者请参阅文献[96]. 3) 逆函数扩张构造 2014年,Carlet和唐灯等人[102]利用F22k-1上的逆函数是APN函数这一特性,构造了F22k上一大类 4差分置换同样可以通过计算差分谱、扩展Walsh谱、Γ-秩、Δ-秩和各种形式的自同构群等CCZ等价不变量来判断它们之间的等价性,最常见的是计算Walsh谱和差分谱.具有五谱值的4差分置换和从逆函数出发构造的4差分置换这2类相互之间的CCZ不等价性一般可以通过计算Walsh 谱来证明或者验证,因为从逆函数出发构造的4差分置换一般不是五谱值的.而在每一大类里各自不同构造之间的CCZ不等价性多数情况下是通过在小域上计算Walsh谱或者差分谱来验证的.接下来我们主要描述该方面的理论结果. 首先,具有五谱值的4差分置换之间的等价性研究相对较少.由于函数存在域的不同,Bracken-Leander函数、Bracken-Tan-Tan函数与其他2类基础构造是CCZ不等价的.其次,由于F2n上一个函数的CCZ等价类里至多包含24n2+2n个函数,而BI 4差分置换里至少有2(2n+2)/3个函数,因此BI 4差分置换里至少含有2(2n+2)/3-4n2-2n个不同的CCZ等价类[91].再次,唐灯和Carlet等人通过差分谱证明了BI 4差分置换与Carlet-Tang-Tang-Liao函数这两大类4差分置换分别与二次函数是CCZ不等价的,并分别从这2类4差分置换中找出了一些子类在理论上证明了这些子类与逆函数是CCZ不等价的[101].最后,陈玺等人提出投影差分谱的概念,将所研究的函数投影到低维空间上,检验其投影函数的投影差分谱是否满足2个CCZ等价函数投影差分谱所满足的必要条件,并通过该方法证明了所有 Carlet-Tang-Tang-Liao函数与逆函数是CCZ不等价的[103]. 本节简单地回顾低差分函数在实际密码算法中的应用. 在Nyberg和Knudsen设计的64 b类似DES的KN密码中,使用了域F233上二次单项式x|→x3[104].但随后Jakobsen和Knudsen利用x3函数代数次数太低的弱点提出了高阶差分攻击[105],攻破了KN 密码.KASUMI算法[106]使用了64 b的8轮DES -类置换,FO和FL是其中的2轮置换.FO函数是一个32 b置换,它由含有FI轮置换的3轮MISTY型变换所组成.FI函数是一个4轮非平衡MISTY-type变换所组成的16 b置换,它由一个7 b APN置换与一个9 b APN置换组成. 1998年NIST发起了一场为了建立新分组密码标准的比赛,由比利时密码学家Daemen和Rijmen设计的Rijndael算法最终胜出,被遴选为AES算法[107].AES算法使用的S -盒是有限域F28上逆函数的仿射变换,这个4差分置换[108]达到了8维空间上已知最优的差分均匀度和已知最优的非线性度.除了AES算法以外,Camellia算法[109]、PRESENT算法[110]、PRINCE算法[111]、LED算法[112]等近期设计算法中均使用了逆函数作为S盒. FIDES是Bilgin等设计的认证加密算法[113],其置换由32个Dillon等发现的APN置换组成.该APN置换的代数次数是4,非线性度与逆函数的非线性度相同均为16,同样达到已知最大非线性度.这表明对该函数的差分攻击和线性攻击与逆函数的情况类似.但FIDES算法的构造设计存在缺陷.Dinur和Jean[114]使用猜测-决定攻击破译了FIDES算法,该攻击基于线性层中扩散上的弱点,S -盒的差分性质对这种攻击完全不起作用.该结果表明,密码算法设计即使使用密码学性质良好的低差分置换,也还需要精心设计密码结构,避免存在安全缺陷. 综上所述,近年来国内外学者在有限域上低差分函数研究方面已经取得了许多重要的结果,但仍有许多问题亟需进一步的研究.例如已有PN函数和APN函数构造都集中在幂函数和二次函数,如何构造一个(CCZ等价意义下)非二次的多项式PN函数和APN函数是低差分函数研究中的一个非常重要的问题.还有,已知的PN幂函数和APN幂函数列表是否完全?二次PN函数和APN函数的CCZ等价类个数是否随变元个数增长而呈指数增长?“大APN问题”,即一般偶扩张上是否存在APN置换的问题,还远没有解决.另外,能否构造与Gold函数具有不同Walsh谱的二次APN函数类也是一个非常有趣的问题.最后,尽管人们在偶扩张已经构造了大量的4差分置换,但像逆函数那样多种密码学指标折衷最优的密码函数的构造还很匮乏.另外,已知偶扩张上4差分置换无限类要么是从逆函数出发构造的,要么与Gold函数联系紧密,能否通过其他的方法进行构造是非常有趣的问题.所有这些问题都值得我们继续深入研究.3.4 大APN问题
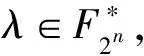
4 4差分置换
4.1 已有构造






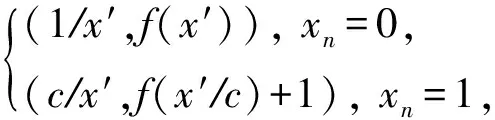

4.2 等价性研究
5 应 用
6 总 结

