“减肥法”妙解大系数的一元二次方程

江苏省扬州市梅岭中学九（10）班 叶初胤

在平时的学习中，我们遇到了很多用一元二次方程解决实际问题的试题.所列的一元二次方程中，一次项的系数和常数项的绝对值比较大，我们可称之为“大系数”.如何妙解含有“大系数”的一元二次方程？今天我来介绍一种“减肥法”.

下面的例题是2017年铜仁市中考试卷的第23题，题目如下：

某商店以20元/千克的单价新进一批商品，经调查发现，在一段时间内，销售量y（千克）与销售单价x（元/千克）之间为一次函数关系，如图所示.

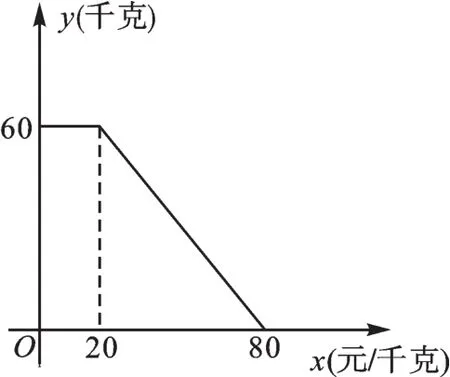
（1）求y与x的函数表达式；

（2）要使销售利润达到800元，销售单价应定为每千克多少元？

【解析】本题考查了一元二次方程在销售方面的应用.

（1）需要分类讨论，分0＜x≤20与20≤x≤80两种情况，当20≤x≤80时，利用待定系数法，即可得到y与x的函数表达式.

（2）根据“每件商品的利润×销量数量=总利润”列出一元二次方程，解方程即可得到销售单价，最后按照所要满足的条件进行检验即可.

解：（1）当0＜x≤20时，y=60；

当20≤x≤80时，设y与x的函数表达式为y=kx+b，把点（20，60），（80，0）代入，可得：

∴y与x的函数表达式为

（2）若销售利润达到800元，根据题意，得：

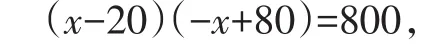
化简为：x2-100x+2400=0，

解得：x1=40，x2=60.

答：要使销售利润达到800元，销售单价应定为每千克40元或60元.

那么如何妙解“大系数”方程x2-100x+2400=0呢？其实用公式法、配方法都是很麻烦的，能力强的同学可以直接用因式分解法——十字相乘法.

我们可以这样做：先将一次项系数除以10，再将常数项除以100（即10的平方），由此得到了新方程为x2-10x+24=0.再逆向思考或者用“十字相乘法”进行因式分解，可知：x2-10x+24=（x-4）（x-6），所以方程x2-10x+24=0易解得：x1=4，x2=6.然后将这两个根分别再乘10，就得到了原方程的解：x1=40，x2=60.

这个方法是不是很巧妙啊？那么这里包含着什么原理呢？让我们来做验证.

假设x2-px+q=0的两个根分别为m、n，根据一元二次方程根与系数的关系，得到m+n=p，mn=q.如果一个含有“大系数”的方程x2-bx+c=0的两根分别是m、n的k倍，则x2-bx+c=0的两个根分别为km、kn，那么两根之和为b=km+kn=k（m+n）=kp，两根之积为c=km×kn=k2（mn）=k2q.我们再把两个方程列表对比：

两根之积q c=k2q方程___x2-px+q=0_____x2-bx+c=0____方程的两根_m，n________km，kn______两根之和p b=kp

由此可见，我们将方程x2-bx+c=0的一次项系数除以k，并把常数项除以k2，由此得到新方程为x2-px+q=0，而方程x2-bx+c=0的两个根分别为方程x2-px+q=0的两个根的k倍.这就是“减肥法”的妙处所在.

好了，下面请你也来试一试，请用才学到的“减肥法”妙解下面的中考题：

（2018·遵义）在水果销售旺季，某水果店购进一优质水果，进价为20元/千克，售价不低于20元/千克，且不超过32元/千克.根据销售情况，发现该水果一天的销售量y（千克）与该天的售价x（元/千克）满足如下表所示的一次函数关系._____________________________

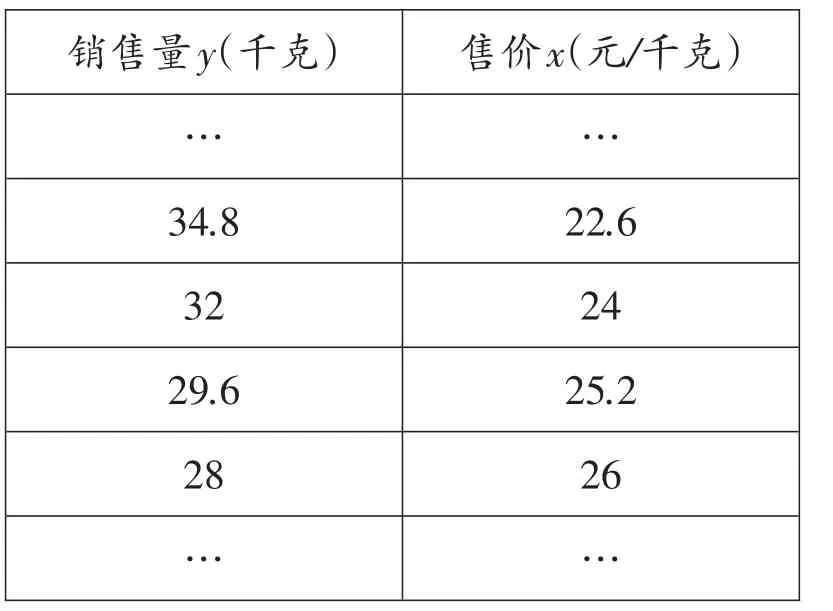
售价x（元/千克）…22.6 24 25.2 26…销售量y（千克）…34.8 32 29.6 28…

（1）某天这种水果的售价为23.5元/千克，求当天该水果的销售量.

（2）如果某天销售这种水果获利150元，那么该天水果的售价为多少元？

【解析】（1）根据表格内的数据，利用待定系数法可求出y与x之间的函数表达式，再代入x=23.5即可求出结论；

（2）根据总利润=每千克利润×销售数量，即可得出关于x的一元二次方程，解之取其较小值即可得出结论.

解：（1）设y与x之间的函数表达式为y=kx+b，

将点（22.6，34.8）、（24，32）代入y=kx+b，得

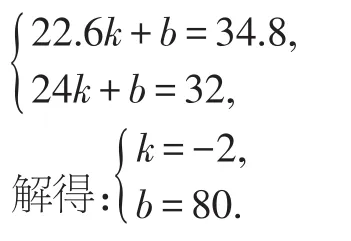
∴y与x之间的函数表达式为y=-2x+80.

当x=23.5时，y=-2x+80=33.

答：当天该水果的销售量为33千克.

（2）根据题意得：（x-20）（-2x+80）=150，

整理得：x2-60x+875=0，

解得：x1=35，x2=25.

答：如果某天销售这种水果获利150元，那么该天水果的售价为25元.

请你认真思考一下，在解方程x2-60x+875=0时，先将一次项系数除以多少，再将常数项除以多少，就可以用“减肥法”求得这个方程的根？

下面，请你用所学的“减肥法”解决一道今年的中考题.

（2018·德州）为积极响应新旧动能转换，提高公司经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元.经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台.假定该设备的年销售量y（单位：台）和销售单价x（单位：万元）成一次函数关系.

（1）求年销售量y与销售单价x的函数表达式.

（2）根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润，则该设备的销售单价应是多少万元？

参考答案：

解：（1）设年销售量y与销售单价x的函数表达式为y=kx+b（k≠0），

将点（40，600）、（45，550）代入y=kx+b，得：

∴年销售量y与销售单价x的函数表达式为y=-10x+1000.

（2）设此设备的销售单价为x万元/台，则每台设备的利润为（x-30）万元，销售数量为（-10x+1000）台，根据题意，得：

整理，得：x2-130x+4000=0，

解得：x1=50，x2=80.

∵此设备的销售单价不得高于70万元，

∴x=50.

答：该设备的销售单价应是50万元/台.

教师点评

数学的乐趣在于深入研究和横向联系.这篇文章结合一元二次方程根与系数的关系，探究了“减肥法”解决“大系数”方程的依据和一般方法，是对一元二次方程的四种通用解法的有效补充.