中考里的“根与系数的关系”

王云峰

如果x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两个实数根，那么这就是一元二次方程根与系数的关系.熟练掌握这一知识点，对我们的解题非常有帮助.下面就让我们走进2018年中考，领略一下她的风采吧！

例1 （2018·江苏盐城）已知一元二次方程x2+kx-3=0有一个根为1，则k的值为（ ）.

A.-2 B.2 C.-4 D.4

【分析】直接利用根与系数的关系求解.

解：设方程的另一个根为x1.

则由根与系数的关系，得：

解得x1=-3，k=2.

故选：B.

【点评】已知一元二次方程的一个根求字母系数的值，可利用一元二次方程根与系数的关系求解，这种方法有时比根的定义法（即将根代入方程）求解简便.

【分析】直接利用一元二次方程根与系数的关系求解即可.

解：设已知方程的另一个根为x1.

则由根与系数的关系，得：

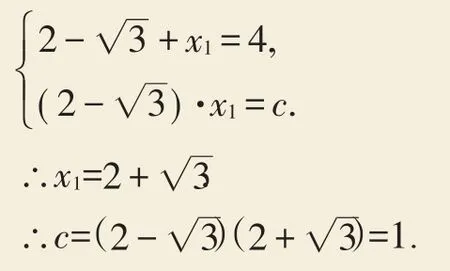
故选：A.

【点评】本题利用一元二次方程根与系数的关系求解比用根的定义法求解简便.

变式2 （2018·江苏南京）设x1，x2是一元二次方程x2-mx-6=0的两个根，且x1+x2=1，则x1=______，x2=______.

【分析】先由x1+x2=1求出m的值，再解方程得到x1，x2的值.

解：由根与系数的关系，得：

x1+x2=m.

又∵x1+x2=1，

∴m=1.

∴已知方程为x2-x-6=0.

即（x-3）（x+2）=0，

解得x1=-2，x2=3.

【点评】求一元二次方程的两根，先利用根与系数的关系确定出一元二次方程中字母系数的值，然后解方程得到两根.

例2 （2018·广西贵港）已知α、β是一元二次方程x2+x-2=0的两个实数根，则α+β-αβ的值是（ ）.

A.3 B.1 C.-1 D.-3

【分析】直接将α+β，αβ的值代入所求的代数式即可求解.

解：由根与系数的关系，得：

故选：B.

【点评】将代数式中的两根互换后，代数式不变，这样的代数式习惯上称为“对称代数式”，求“对称代数式”的值利用一元二次方程根与系数关系求解比较快捷.

变式1（2018·四川眉山）若α，β是一元二次方程3x2+2x-9=0的两根，则的值是（ ）.

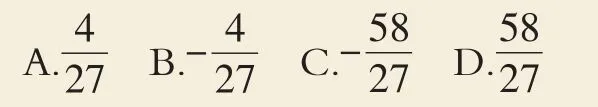
【分析】将变形为用含α+β，αβ表示的代数式，再利用一元二次方程根与系数的关系求解即可.

解：由根与系数的关系，得：

故选：C.

【点评】利用一元二次方程根与系数的关系求“对称代数式”的值，有时需要将被求的代数式变形，变形为用两根之和、两根之积表示的代数式.

变式2 （2018·江西）一元二次方程x2-4x+2=0 的两根为 x1，x2，则的值为_______.

【分析】利用一元二次方程根与系数的关系以及方程的根的定义求解.

解：∵x1，x2是x2-4x+2=0的两根，

【点评】若待求值的代数式不是“对称代数式”，这时可考虑综合利用根与系数的关系、方程根的定义求解.

例3 （2018·贵州遵义）已知x1，x2是关于x的方程x2+bx-3=0的两根，且满足x1+x2-3x1x2=5，那么b的值为（ ）.

A.4 B.-4 C.3 D.-3

【分析】将x1+x2，x1x2的值代入x1+x2-3x1x2=5即可求解.

解：由根与系数的关系，得：

解得b=4.

故选：A.

【点评】已知“对称代数式”的值，利用根与系数的关系，可求方程中字母系数的值.

变式1（2018·山东烟台）已知关于x的一元二次方程x2-4x+m-1=10的实数根x1，x2满足3x1x2-x1-x2＞2，则m的取值范围是_______.

【分析】将x1+x2，x1x2的值代入3x1x2-x1-x2＞2求解，另外还要考虑b2-4ac≥0这一个隐含条件对m的限制.

解：由根与系数的关系，得：

解得m＞3.

由题意，得：

表10“方差方程的Levene检验”列方差齐次性检验结果：F值为0.4781，显著性概率为0.5050，大于0.05，因此两组方差不显著。

解得m≤5.

综上，m的取值范围是3＜m≤5.

【点评】在利用一元二次方程根与系数的关系求一元二次方程中字母系数的取值范围时，考虑问题要全面，不能忽视隐含条件b2-4ac≥0对字母系数的限制.

变式2（2018·湖北十堰）已知关于x的一元二次方程x2+（2k-1）x+k2+k-1=0有实数根.

（1）求k的取值范围；

（2）若此方程的两实数根x1，x2满足=11，求k的值.

解：（1）由题意，得：

（2）由根与系数的关系，得：

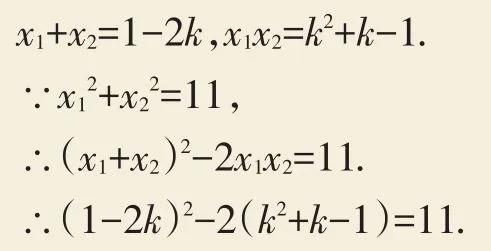
整理得：k2-3k-4=0，

分解因式得：（k-4）（k+1）=0，解得k=-1或4.

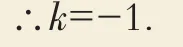
【点评】利用一元二次方程根与系数的关系的前提条件是b2-4ac≥0，即一定要保证一元二次方程有实数根.此外，在求出字母系数的值后一定要检验.