管窥中考回归教材

王 磊

随着六大核心素养的提出，中考中对一元二次方程的考查形式有了新的动向.其中，对应用的考查，既重视基础知识，又加大了对逻辑推理、直观想象等方面能力的考查，往往还会结合一些生活情境.现通过对两道中考题的分析，帮助同学们掌握相关的解答技巧.

一、中考例题

例1 （2018·贵州安顺）某地2015年为做好“精准扶贫”，投入资金1280万元用于异地安置，并规划投入资金逐年增加，2017年在2015年的基础上增加投入资金1600万元.

（1）从2015年到2017年，该地投入异地安置资金的年平均增长率为多少？

（2）在2017年异地安置的具体实施中，该地计划投入资金不低于500万元用于优先搬迁租房奖励，规定前1000户（含第1000户）每户每天奖励8元，1000户以后每户每天奖励5元.按租房400天计算，求2017年该地至少有多少户享受到优先搬迁租房奖励.

【解析】（1）设年平均增长率为x，根据2015年投入资金×（1+增长率）2=2017年投入资金，列出方程求解即可.

（2）设今年该地至少有a户享受到优先搬迁租房奖励，根据前1000户获得的奖励总数+1000户以后获得的奖励总和≥500万，列不等式求解可得.

【解答】（1）设该地投入异地安置资金的年平均增长率为 x，根据题意得 1280（1+x）2=1280+1600，解得：x=0.5或x=-2.5（舍去）.

答：从2015年到2017年，该地投入异地安置资金的年平均增长率为50%.

（2）设2017年该地有a户享受到优先搬迁租房奖励，根据题意得，

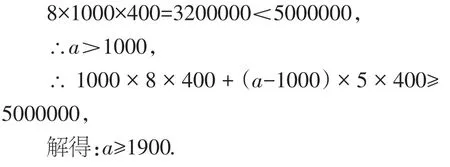
答：2017年该地至少有1900户享受到优先搬迁租房奖励.

【点评】本题从生活的角度考查了一元二次方程的应用.第一问属于常规题，同学们在平时的学习中注意训练，应该可以较为顺利地解决这个问题.第二问需要同学们有一定的数学阅读和分析能力：首先要能够判断出享受到优先搬迁租房奖励的住户是否超过1000人；

其次，要能够将享受到优先搬迁租房奖励的住户分为两类，按照两种价格结算，分类列出不等式，完成解答.通过本道题，同学们还可以了解到我国现行的相关政策.这是一道很有实际意义的考题.

例2 （2018·湖北黄冈）一个三角形的两边长分别为3和6，第三边长是方程x2-10x+21=0的根，则三角形的周长为_______.

【解析】将已知的方程x2-10x+21=0左边分解因式，利用两数相乘积为0，两因式中至少有一个为0，将原方程转化为两个一元一次方程，求出一次方程的解，得到原方程的解为3或7.再利用三角形的两边之和大于第三边进行判断，得到满足题意的第三边的长，从而求得三角形的周长.

【解答】将x2-10x+21=0因式分解得：（x-3）（x-7）=0，解得：x1=3，x2=7.

∵三角形的第三边是x2-10x+21=0的根，

∴三角形的第三边为3或7.当三角形第三边为3时，3+3=6，不能构成三角形，舍去；当三角形第三边为7时，三角形三边分别为3，6，7，能构成三角形，则第三边的长为7.

∴三角形的周长为：3+6+7=16.故答案为：16.

【点评】本题考查了利用因式分解法求解一元二次方程，以及三角形三边的关系.利用因式分解法求解一元二次方程时，首先将方程右边化为0，左边分解因式，然后利用两数相乘积为0，两因式中至少有一个为0，将原方程转化为两个一元一次方程来求解.

二、变式练习

变式一：某市从2018年开始大力发展“西游文化”旅游产业.据统计，该市2018年“西游文化”旅游收入约为2亿元.预计2020年“西游文化”旅游收入达到2.88亿元，据此估计该市2018年～2020年“西游文化”旅游收入的年平均增长率约为（ ）.A.2% B.4.4% C.20% D.44%

【解析】设增长率为x，根据2018年旅游收入×（1+增长率）2=2020年旅游收入，列出方程求解即可.

【解答】C.

【点评】解决本类题，认真审题很重要，从题干中发现这是一个一元二次方程的应用问题是关键，选用直接开平方法计算答案是高效率的方法.通过对题目的提炼可以整理得到方程——2（1+x）2=2.88，解该方程得到答案是0.2，故答案选择C.

变式二：欧几里得的《原本》记载，形如x2+ax=b2的方程的图解法是：画Rt△ABC，使再在斜边AB上截取则该方程的一个正根是（ ）.

A.AC的长 B.AD的长

C.BC的长 D.CD的长

【解析】将x2+ax=b2利用配方法变形得到：变形得到完全平方形式（x+直接开平方后得到因为要求正根，所以只保留的

a2形式，根据题意，线段AB的长是 b2+4，所以的长就是线段AB的长度减去线段BD的长度，因此答案选择B.

【解答】B.

【点评】本题考查了数形结合的数学思想，还考查了配方法解一元二次方程和勾股定理等知识.同学们需要在理解代数方法的基础上，融入几何思考，能够将抽象的式子直观地展示为几何图形.这是一道非常好的培养同学们几何直观素养的考题.