常压立式钢制储罐沉降测量方法的研究

季 鹏，李绪丰

(广东省特种设备检测研究院，广东 佛山 510655)

1 基本概况

在国内常压储罐不属于特种设备的管辖范围，对常压储罐的管理也主要是业主自行监管。近些年来，出现一些重大的储罐安全事故，国家和各地区的安全监察管理部门加大了对危化品的常压储罐的监管力度。一些地区的监管部门出台了相关的关于危化品常压储罐监管规程，加大了对各罐区的安全隐患排查，并督促业主对常压储罐进行定期检验。在国内外也有关于在用常压储罐检验的标准，如：API653《Tank Inspection,Repair,Alteration,and Reconstruction》，SY/T6620《油罐的检验、修理、改建及翻建》等。

2 储罐沉降

储罐的沉降测量，也是对储罐定期检验中的一种常用的检验方法。由于储罐下方的地质结构以及建造时储罐基础的质量，在使用一段时间之后，都会导致储罐沉降。沉降会引起储罐局部应力增加，影响储罐的结构稳定，严重时会导致储罐局部开裂或坍塌。根据沉降对储罐部位的影响，储罐沉降的主要类型与储罐罐壁和罐底板相关。罐底板的沉降需要进入罐内进行测量，本测量方法的中不做介绍。

罐壁的沉降分为均匀沉降、平面倾斜(刚形体倾斜)和偏离平面沉降。均匀沉降不会给储罐造成结构上的应力，但是会对与储罐连接的接管和附件产生影响；平面倾斜会使储罐在倾斜的平面上翻转，影响液位升高，由此会增加罐壁的环向应力。另外倾斜过大能导致浮顶的周向密封出现粘和现象，从而阻止罐顶的移动。同时也会影响与储罐连接的接管；偏离平面沉降可能会导致罐壁顶部出现椭圆度，而罐壁的偏离平面沉降幅度取决于椭圆度的范围，可能会阻碍浮顶的正常运行。测量偏离平面沉降是为了确保罐壁和罐底结构完整性而需要确定和评价的主要因素。基于这样的原则，一种常用的方法是针对储罐周边上的各个数据点确定均匀沉降幅度和平面倾斜幅度。如果能够判断确定出现了一个平面倾斜平面，该平面倾斜平面就是一个非常重要的基准点，根据这个基准点就可以测量偏离平面沉降幅度。

3 罐壁沉降

罐壁沉降测量的目的是找出各个沉降观察站的高程差，利用最小二乘法最佳拟合曲线，找出最大沉降值是否在允许范围之内。首先目视罐壁周围，找出沉降较大的区域，这些沉降较大的区域置于沉降测量站之内。每个站点的测量位置根据现场情况确定，可以选择测量第一层和第二层罐壁焊缝的高程差。站点的数量根据储罐的直径来决定，把罐壁弧长均等分成N个站点，N根据以下公式确定：

N=D/10

式中：D:储罐直径，单位ft；N:储罐测量站点的最低要求，最小为8，所有值精确到下一个更大的偶数，沉降点之间的弧长不超过32ft。

3.1 最小二乘法拟合余弦曲线

按偏差平方和最小的原则选取拟合曲线，并且采取二项式方程为拟合曲线的方法,称为最小二乘法。如下公式：

通过测量的数据，最佳拟合曲线图形的现可以通过matlab中的plot命令实现。可以得出最佳拟合余弦曲线：

Elevpred=a+b×cos(θ+c)

a、b、c是通过拟合之后的出来的常数。但要注意的是，使用最佳拟合曲线时，重合度R2需要大于或者等于0.9，才能认为最佳余弦曲线为有效曲线。因此，在对测量完的数据进行最佳拟合余弦曲线后，需要计算出最佳余弦的重合度是否满足要求。

3.2 储壁沉降允许值

(1)在API653标准中，提到当采用最佳余弦拟合曲线评估储罐沉降时，允许偏离平面沉降的最大值：

Smax=(L2×Y×11)/(2×E×H)

式中：S为允许偏离平面沉降 ft；L 为测量点之间的弧长 ft；Y为罐底材料的屈服强度 lbf/in2；E 为弹性模量lbf/in2;H 为储罐高度ft。

(2)当无法得到清晰的平面倾斜或超过上述测得的最大偏离平面沉降时，可以利用以下公式计算最大允许偏离平面沉降Smax,in=min[K×Sarc×(D/H) ×(Y/E),4.0]

K为常数;Smax,in为允许偏离平面沉降测量in; Sarc有效沉降弧长 ft；D储罐直径 ft。

3.3 罐壁沉降点与最佳余弦拟合曲线的图解

展开储罐测量点图与最佳拟合余弦曲线对应，可得出下图1。

图1 罐壁沉降测量图解

Ui为i点的偏离平面沉降，“i”点的偏离平面偏转量为Si=Ui-(1/2Ui-1+ 1/2Ui+1)，找出Si与最佳拟合余弦曲线的差值，即为罐壁沉降测量最大差值。

4 罐壁沉降测量实例

4.1 测量结果未超出允许范围

如：A储罐直径140ft，高度48ft拱顶，碳钢材料，弹性模量为29000000psi，屈服强度30000psi。数据见表1。

表1 A储罐数据表 (单位in)

最佳拟合余弦曲线方程式ELpred=-5.0+4.5×cos[(2πχ/440+2)- π/2]，Ui= ELactual,i- ELpred,i，Si=Ui-(1/2Ui-1+ 1/2Ui+1)，Syy为平均高程测量值和高程测量值之差的平方和，SSE为高程测量值和高程预测值之差的平方和。

重合度R2=( Syy-SSE)/Syy=0.99>0.9,满足使用最佳拟合余弦曲线的条件。

根据罐壁大允许沉降公式计算可以得出Smax为1.44in，从表1中可以看出测量出来的最大偏离平面沉降为0.77in(第5点位置)，比较最大允许值(1.44in)可知，储罐罐壁沉降在允许范围之内。

4.2 测量结果未超出允许范围

如B储罐直径150ft，高度40ft浮顶储罐，碳钢材料，弹性模量为29000000psi，屈服强度30000psi。数据见表2。

表2 B储罐数据表(单位in)

绘制出来的最佳拟合余弦曲线ELpred=-3.70+3.52×cos[(2πχ/471.24+4)- π/2]；弧长L=150×π/16=29.45ft；允许的最大沉降Smax=(29.45)2×30000×11/[2×(29000000×40)]=0.123ft=1.48in。

从表1中可以看出测量出来的最大偏离平面沉降为2.07in(第1点位置)，大于允许最大值(1.48in)，这是需要用3.2(2)中的方式计算最大允许值。

从图2沉降图解中可以看到，最佳拟合预先曲线与实测曲线的交点在第7点和第8点之间，第1点到相交点的弧长Sarc,7=7.0×29.45=206.17ft 到Sarc,8=8.0×29.45=235.62ft之间。

根据3.2(2)中的公式，由于直径为150ft，K值用4.0代入，计算得出的最大允许偏离平面沉降Smax,in范围在2.39～3.20in之间。

图2 测量结果未超出允许范围的沉降图解

4.3 重合度小于0.9的曲线

如C储罐直径120ft，高度40ft外浮顶储罐，碳钢材料，弹性模量为29000000psi，屈服强度34000psi。测量数据见表3。

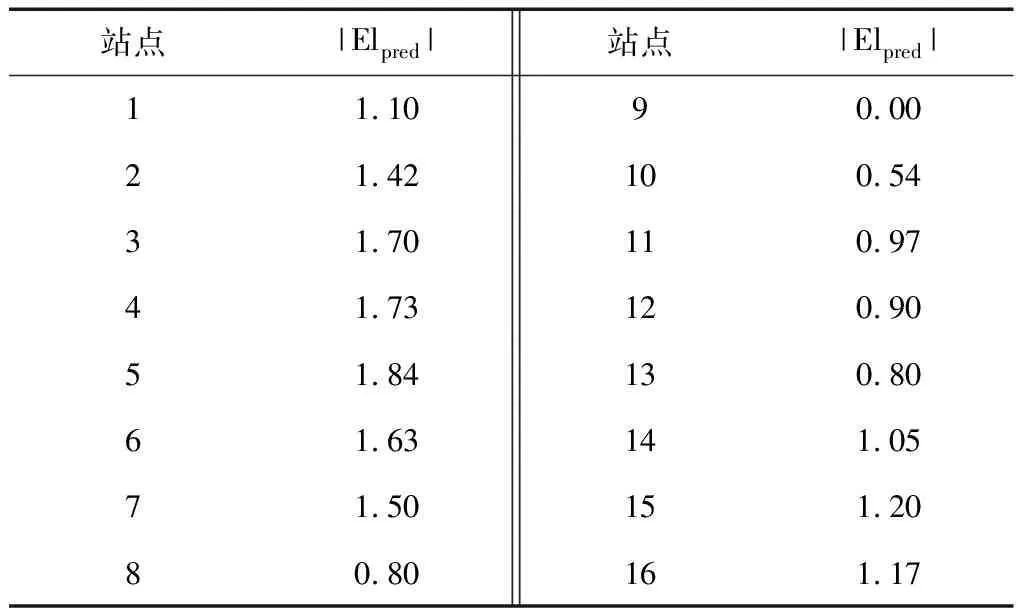
表3 C储罐数据表(单位in)

把测量值绘制成沉降图解，见图3。从图中可以看出第5点和第11点沉降偏差较大，这是需要增加沉降测量点。增加的位置为沉降突变点周围及较大沉降点附近，增加沉降测量点的位置在之前测量点中间。在第2、第5、第9、第11、第13点附近增加测量沉降点,增加点见图3中白点。测量值连城曲线。从图中可以看出沉降点5的弧长Sarc5,1为7L，最大偏离平面沉降Smax5,1为1.32in；沉降点11的弧长4 L最大偏离平面沉降Smax3,1为0.6in。

图中黑点为实测沉降值，白点为增加测量沉降点值

根据3.2(2)中的公式，由于储罐是直径为120ft的外浮顶储罐，K值用6.5代入，分别计算得出第5点和第11点的最大允许偏离平面沉降为3.77in和2.16inin。比较测量与允许最大偏离平面沉降值，可知此储罐沉降在允许范围之内。

5 结束语

通过有效的测量方法，采用最佳拟合余弦曲线，来对储罐进行沉降测量和评估，可以及时了解储罐因沉降引起的应力集中和储罐的稳定性是否在可接受范围之内，可有效地预防因严重沉降引起的劣化及安全事故发生。