大跨公轨两用悬索桥主缆线形的参数敏感性分析

杜 斌,张 兴,杨 令,雷 民

(1.贵州顺康路桥咨询有限公司,贵阳 550000； 2.贵州大学,贵阳 550025)

贵州省是一个多山深谷及喀斯特地貌广泛分布的省份，省内的城市轨道交通宜采用轻轨方案，虽然有轨电车基本上采用地面运行方式，但是在需要跨越沟谷河流的时候，仍需采用桥梁方案，这一问题在贵州的多山深谷地区会显得十分突出。同时，为了节省投资，缩短工期，还会在桥梁中采用有轨电车与市政道路共用交通线路的方式，即采用公轨两用桥梁[1]。兴义市的马岭河3号特大桥是连接兴义市和义龙试验区的重要交通要道，跨径组成为(166+450+157) m，矢跨比为1/9，结构形式为半漂浮式单跨钢桁架加劲梁地锚式公轨两用悬索桥，如图1所示。该项目是公轨两用桥梁以及公轨两用悬索桥在贵州省内的首次应用。

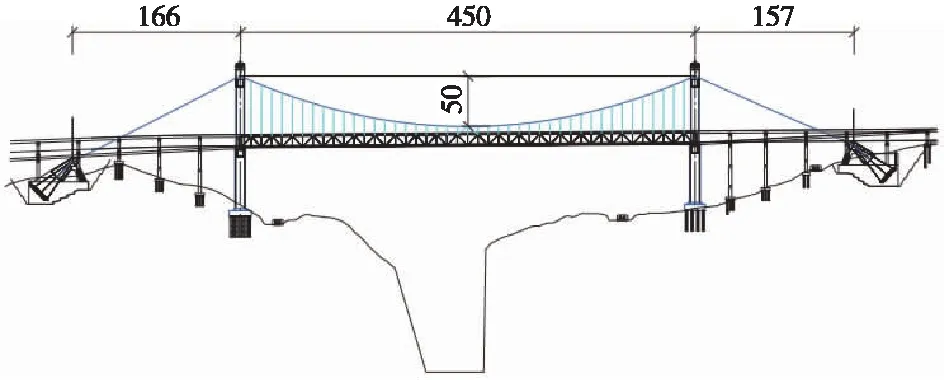
图1 马岭河3号特大桥布置(单位：m)

公轨两用悬索桥荷载大，荷载形式复杂，为了轨道交通的舒适性和安全性，减轻运营中因桥面不平顺激发的桥梁振动，一个高质量的成桥线形是必不可少的[2]。因此，公轨两用悬索桥对线形控制的精度要求相比普通的公路悬索桥更高，也对本项目的施工监控工作提出了更高的要求。根据以往悬索桥施工监控工作的经验，在施工过程中，主缆线形受众多因素的影响，容易出现偏离设计目标的情况，为了使主缆线形尽可能接近设计状态，需要提前制定有效的调整措施[3]，因此需要提前掌握各个参数对悬索桥线形控制的影响程度，根据影响程度的不同，做到把握重点，有的放矢。

在主缆线形计算方面，文献[4]建立了悬索桥主缆线形计算的精确理论——分段悬链线理论；文献[5]对文献[4]中存在不收敛的情况进行了讨论，并提出了一种收敛的算法；文献[6]探讨了单圆曲线索鞍位置计算；文献[7]将文献[6]探讨的算法，推广到复合圆曲线索鞍位置的计算，并进行相应的改进；文献[8]对空间缆索悬索桥的主缆线形进行了分析，提出了一种考虑主缆和吊索的耦合效应以及索鞍影响的数值解析法，并对该方法精度进行了论证；文献[9]根据主缆无应力长度不变的原则，基于空间分析模型，研究了自锚式悬索桥空间主缆线形的精确计算方法。至此悬索桥主缆线形计算方面的发展已趋于完善。

对于主缆线形的敏感性参数方面的研究较少，文献[10]探究了主缆架设中影响跨中主缆高程的影响参数；文献[11]以有限元模型为基础，探究了主缆高程和吊杆力的影响参数，得出主缆弹性模量、加劲梁自重、主缆自重是其主要的影响参数的结论；文献[12]以有限元模型为基础，针对主缆弹性模量、主缆自重、温度、散索鞍等对主缆线形的影响进行了研究。

本文以在建的马岭河3号特大桥为研究对象，从施工监控的需要出发，采用解析法和有限元软件相结合的方法，首先对不同的计算理论的结果进行对比分析，然后选择对线形计算影响较大的关键参数进行参数敏感性的分析研究，并根据各个参数在索长指标、内力指标以及架设指标上所体现的不同程度的敏感性进行分类评价，得出的成果可为本项目的施工监控工作提供理论依据和参考。

1 主缆线形计算成果

通过理解设计文件以及与设计方、施工方及材料供应方的沟通，采集各项材料参数和荷载参数如表1所示，根据采集的参数建立有限元分析模型，计算结果如表2所示。与设计文件给出的成桥状态下的跨中高程1 159.024 m，空缆状态下的跨中高程1 164.904 m以及索鞍预偏量-1.072 m/0.924 m相比，本研究的计算结果具有较高精度，将作为本次研究的基准计算结果采用。

表1 设计基准参数

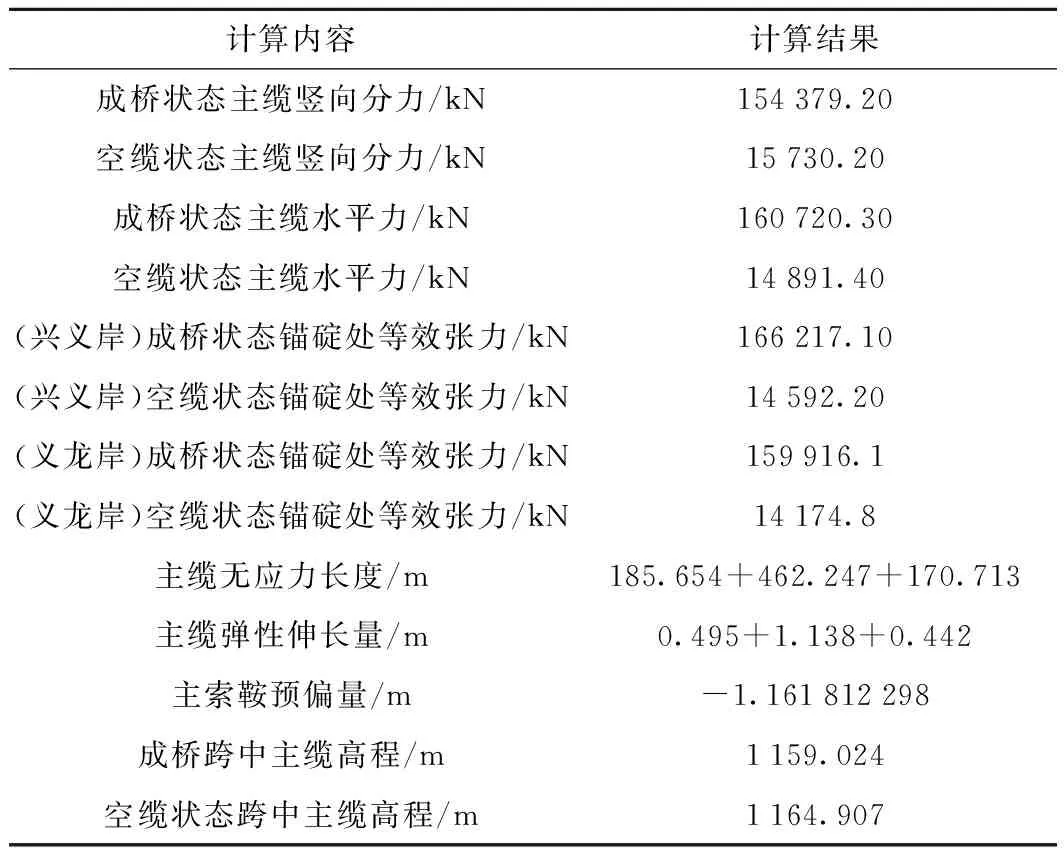
表2 基准计算结果

2 研究参数选取

影响公轨两用悬索桥主缆线形的因素[10]主要分为计算分析理论、材料特性和恒载参数、架设温度等因素。目前悬索桥分析计算软件均采用了非线性有限元分析理论[13]。但各款软件在主缆线形计算上采用的计算方法不尽相同，因此需比较各种方法在线形计算方面的差别，以便采用合适的线形计算理论。但是材料特性、恒载参数等往往与制造密切相关，某些参数偏差具有随机性和偶然性，在设计中无法精确考虑；施工时的环境温度也难以和设计温度保持一致。因此在施工监控环节，分析这些主缆线形对这些参数的敏感性，掌握其影响是非常有必要的，有助于在施工前期准备合适的控制方案，让监控成果尽可能接近设计目标[6]。

3 线形计算的参数敏感性分析

大跨公轨两用悬索桥的线形计算中主要包括主缆无应力索长、索鞍预偏量、主缆高程等几项重要成果，每项成果的质量，均会对主缆架设的质量存在影响。针对这一情况，从计算理论、材料特性、温度场、材料自重、恒载作用等几项参数出发，研究主缆各项计算成果对这些参数的敏感程度，找出高敏感性参数，以便在主缆架设监控工作中进行重点控制。同时可为其他类似工程提供参考。

分析方法采用解析法和有限元软件相结合的方法，解析法以唐茂林、沈锐利、李传习[1，4，14-16]等学者提出的方法为理论依据，有限元软件则以Midas/Civil[17]为主。

3.1 线形计算理论的敏感性分析

分析不同的线形计算方法对主缆高程和无应力索长的影响，通过采用文献[4-5]中的解析法的计算结果进行对比，可知不同方法之间的差距，亦可对现在常用的悬索桥有限元分析软件的计算精度进行掌握。文献[4]中，唐茂林等针对国内多座悬索桥，采用不同计算理论，对主缆的形状长度、水平分力等做了比较。本次研究在前人的基础上，针对传统抛物线理论、分段悬链线理论、节线法理论，对成桥后的主缆各标记点的高程、主缆形状长度、主缆无应力索长、水平分力及弹性伸长量等进行比较，探究主缆线形对线形计算理论的敏感性。表3～表7所示为3种线形计算理论的计算结果的对比，其中分段悬链线理论是文献[4-5]中解析法的理论基础，节线法理论则是Midas/Civil中悬索桥计算的理论基础；抛物线法则是古典的悬索桥的线形计算理论。表3～表7中展示了分段悬链线理论的计算成果，并呈现了其余两种理论与分段悬链线理论在同一计算目标上的差值。

表3 各种计算理论主缆高程 m

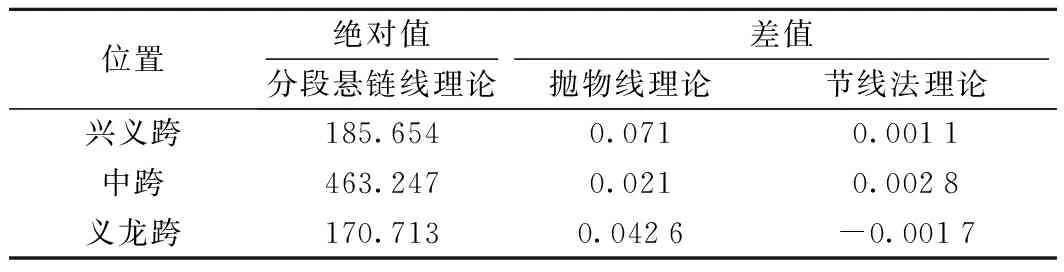
表4 各种计算理论主缆无应力索长 m

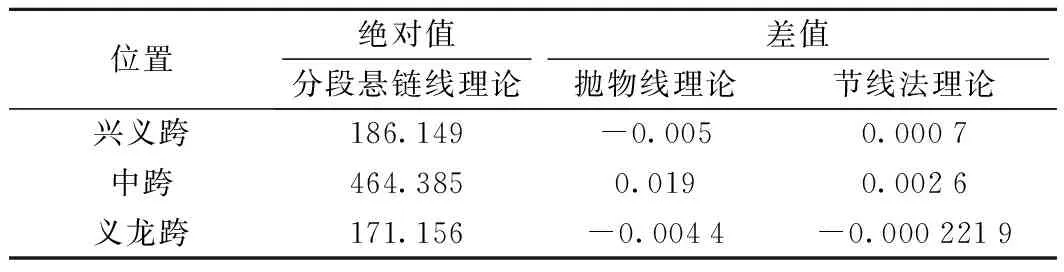
表5 各种计算理论主缆形状长度比较

表6 各种计算理论主缆水平分力比较 kN

表7 各种计算理论主缆弹性伸长量比较 m

从表3～表7可知，主缆线形对计算方法的敏感性极高，不同的计算方法下，主缆线形各项指标均存在较明显的差距，文献[4]已对分段悬链线理论的计算精度进行了论证，结果表明，基于分段悬链线原理的解析法具有求解精度高的特点，在此不做过多论述。基于节线法理论的有限元软件Midas/Civil的计算结果，与解析法的结果相比，计算精度比较接近；而抛物线理论与其他两种理论间最多相差1～2个数量级，在这一级别跨径的悬索桥的主缆计算中已经难以满足工程精度的要求，存在较高的误差，仅适合在快速估算时使用；分段悬链线理论和节线法理论结果较接近，均具有较高的精度，能满足工程建设的要求。这同时也证明使用以节线法理论为基础的有限元分析软件Midas/Civil进行本项目的监控计算是足够精确可靠的。

3.2 主缆材料特性的敏感性分析

主缆由高强钢丝组成，主要的材料特性有强度和弹性模量，由于现行规范中对主缆的安全系数要求较高，主缆的应力均处于低应力的弹性阶段，因此主缆强度对主缆的线形计算无影响。由于主缆钢丝的弹性模量存在一定离散性，这种离散性会影响主缆在荷载作用下的弹性变化状态。因此，针对弹性模量进行敏感性分析，研究主缆无应力索长、主缆内力、索鞍预偏量、主缆高程等对主缆弹性模量的敏感程度。研究时，取主缆弹性模量范围为1.5～2.5 GPa。本桥的弹性模量取2.05 GPa。结果如图2～图7所示。

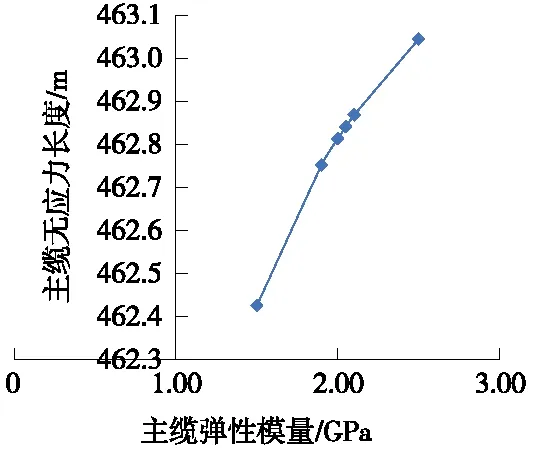
图2 主缆弹性模量对无应力长度的影响

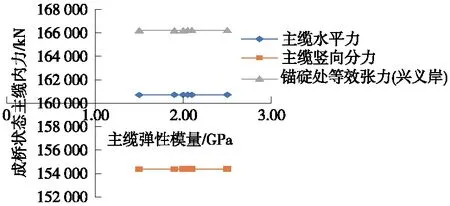
图3 主缆弹性模量对主缆成桥内力的影响

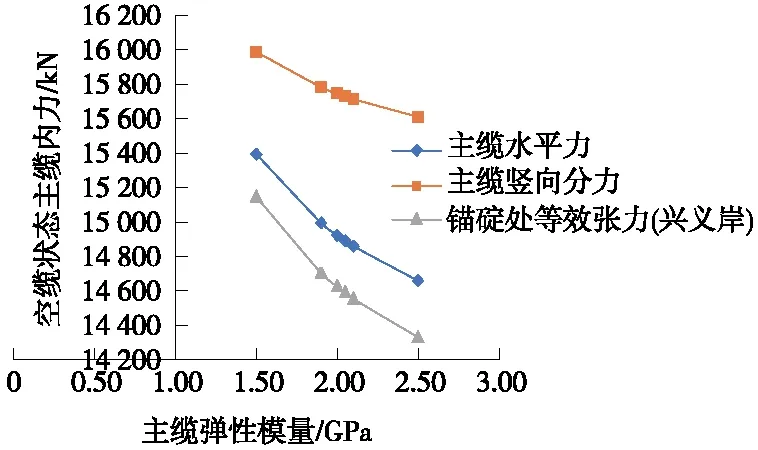
图4 主缆弹性模量对主缆空缆内力的影响

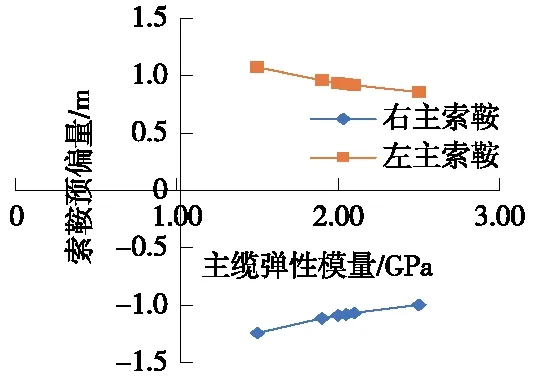
图5 主缆弹性模量对索鞍预偏量的影响

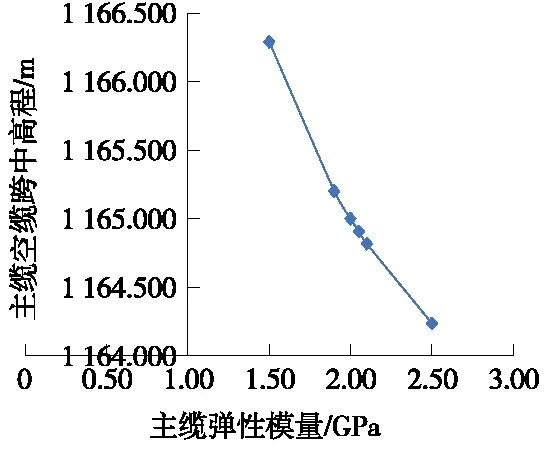
图6 主缆弹性模量对主缆空缆高程的影响

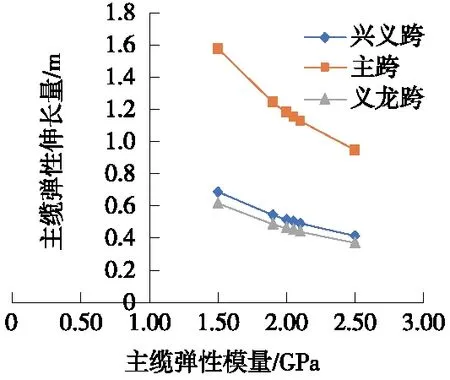
图7 主缆弹性模量对主缆弹性伸长量的影响

由图2可知，主缆弹性模量对主缆无应力长度的影响较明显，随着主缆弹模模量的变化，无应力长度呈近似的线性正相关的变化，弹性模量每提高5%，无应力索长平均增加55 mm。从各线段的斜率可知，当主缆弹模≤2.0 GPa时，弹性模量引起的无应力索长变化的变化率较主缆弹模≥2.0 GPa时高。

由图3可知，主缆弹性模量对成桥状态主缆内力影响量甚微，主缆弹性模量每提高5%，主缆成桥阶段主缆内力仅提高约2 kN。

由图4可知，主缆弹性模量对空缆状态主缆内力影响较明显，各项内力与主缆弹性模量呈近似线形的负相关性，主缆弹性模量每提高5%，空缆状态下，主缆水平分力平均降低约70 kN，竖直方向分力平均降低35 kN，锚碇处张力平均下降约80 kN。

由图5可知，主缆弹性模量与索鞍预偏量呈负相关性，主缆弹性模量越高，索鞍预偏量越小，主缆弹性模量每提高5%，索鞍预偏量平均减小20 mm。

由图6可知，主缆弹性模量与空缆跨中高程呈负相关性，主缆弹性模量每提高5%，空缆跨中高程平均下降200 mm。根据监控精度的要求，主缆的弹模模量造成的高程改变量大，敏感性程度高，属于高敏感性参数。

由图7可知，主缆弹性模量与主缆弹性伸长量呈负相关性，主缆弹性模量每提高5%，主跨弹性伸长量平均减小60 mm，边跨弹性伸长量平均减少20 mm。

3.3 温差的敏感性分析

在主缆架设阶段，温度不仅影响主缆长度，还会引起主塔偏位，这些都将对主缆线形产生影响。在索股架设阶段，难以保证架设温度和设计温度保持一致，为了探索两个温度之间的温差对索股架设质量的影响，本研究在保持参数不变的情况下，计算架设时的环境温度与设计温度的温差在-20～20 ℃之间主缆各项计算成果的变化情况。通过计算对比发现，在不同设计温度下，悬索桥成桥阶段的各项指标均不会发生改变，成桥阶段的主缆内力，无应力索长、弹性伸长量等均保持不变；空缆架设阶段的几项重要指标则有明显改变，这说明，温差对悬索桥监控工作的影响，主要体现在主缆架设阶段。计算结果如图8～图10所示。

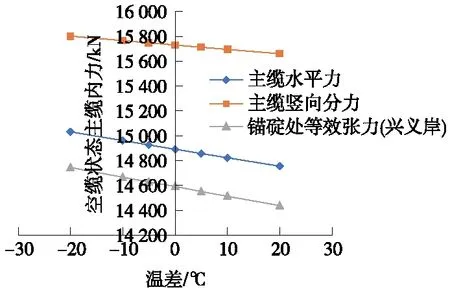
图8 温差对空缆状态主缆内力的影响

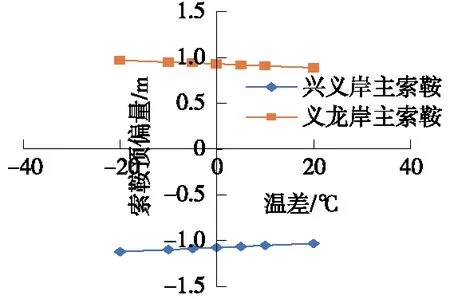
图9 温差对索鞍预偏量的影响

图10 温差对空缆跨中高程的影响

由图8可知，温差每提高1 ℃，主缆空缆状态下，水平分力下降约6 kN，竖向分力下降约9 kN，锚碇处主缆张力下降约7 kN。可见温差对空缆状态的主缆内力敏感性不高。

由图9可知，温差每提高1 ℃，索鞍预偏量减小2.25 mm，看似微小，但是在现场施工中，温差往往较大，在较大的温差下，索鞍预偏量的设置就会造成较大的影响。因此，温差应作为设置索鞍预偏量时的高敏感参数进行关注，在设置索鞍预偏量时，应准确预估架设主缆的季节，根据当地气象资料，合理选取架设温度计算值，尽可能降低温差造成的影响。

由图10可知，温差对空缆高程的影响同样显著，温差每提高1 ℃，空缆高程降低约20 mm，相比由主缆弹性模量造成的影响，主缆弹性模量可通过现场测定和试验进行准确测定，这样即可消除主缆弹性模量的影响，但是温差的影响却是无法避免的。主缆高程对温差的敏感性较高，主缆架设监控时，应密切关注温度的变化。

3.4 主缆荷载的敏感性分析

主缆荷载与主缆丝股数、主缆检修通道、防护涂装等有关，为研究主缆荷载对线形计算的敏感性，保持其他参数不变，研究主缆荷载在50%～150%变化时，主缆各项指标的变化情况。通过对比，主缆荷载对线形计算的影响，主要体现在成桥阶段的主缆内力，空缆阶段的主缆内力以及空缆高程等几项指标上，其余几项参数，如无应力长度、索鞍预偏量等，受主缆荷载的影响量较小，对主缆荷载的变化的敏感性低。结果如图11～图13所示。

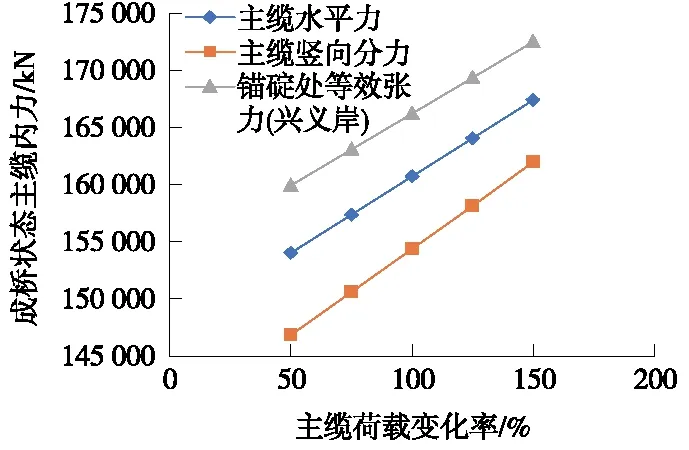
图11 主缆荷载变化率与成桥状态主缆内力的关系

图12 主缆荷载变化率与空缆状态主缆内力的关系

图13 主缆荷载变化率对空缆高程的影响

由图11可知，主缆荷载对成桥阶段的影响较明显，从各线段的斜率分析，增大主缆荷载，主缆的竖向分力增加速率快于水平分力和锚跨张力的增加速率。主缆荷载每增加5%，水平分力提高660 kN，竖向分力提高750 kN，锚碇处张力提高620 kN，因此，通过提高主缆丝股数或增大主缆面积达到提高悬索桥重力刚度的方法，会造成桥塔结构及基础投资的快速增加。

由图12可知，在空缆阶段，主缆荷载基本由自重组成，各项内力的增长并非由荷载造成，而是由不同的索鞍预偏角度，不同的主缆高程所造成的，在本阶段，主缆水平分力和锚碇张力的增长率均高于竖向分力的增长率，但各项内力的单位增加幅度均很小，与成桥状态的内力相比，可忽略不计。

由图13可知，在主缆架设阶段，主缆荷载对空缆高程的影响较明显，主缆荷载每提高5%，空缆高程提高约15 mm。在主缆架设监控工作中，准确测定主缆荷载显得尤为重要，如果存在较大偏差，将会导致最终的成桥线形偏离设计线形。因此，对于空缆高程来说，主缆荷载属于高敏感性参数。

3.5 加劲梁自重的敏感性分析

与主缆荷载不同的是，加劲梁自重荷载是在主缆空缆架设完成后才作用于主缆上，因此，加劲梁自重荷载对空缆阶段的主缆内力的影响不是直接影响，且影响量极小，可不作为敏感参数考虑。加劲梁自重的影响主要体现在成桥阶段主缆内力、无应力索长、弹性伸长量等几项指标上，对于主缆架设阶段的影响，则体现在空缆高程这一指标上。本研究通过对比加劲梁自重在50%～150%变化时，探究主缆各项指标的变化情况。结果如图14～图16所示。

图14 加劲梁自重变化率与成桥状态主缆内力的关系

图15 加劲梁自重变化率与无应力索长的关系

由图14可知，随着加劲梁自重的变化，锚碇张力的增长率最快，水平分力次之，竖向分力最慢。加劲梁自重每提高5%，锚碇张力提高约2 800 kN，水平分力提高约2 750 kN，竖向分力提高约2 600 kN。

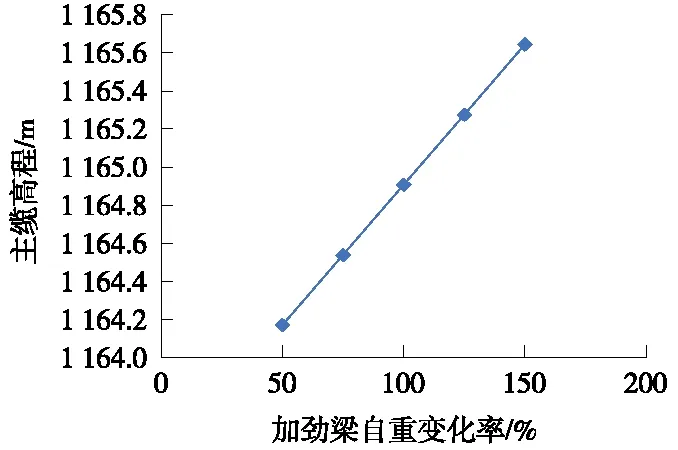
图16 加劲梁自重变化率与空缆高程的关系

由图15可知，主缆无应力索长与加劲梁自重呈反比，加劲梁自重每提高5%，主缆无应力索长缩短约21 mm。

由图16可知，加劲梁自重对空缆高程的影响量明显，加劲梁自重每提高5%，主缆空缆高程提高约74 mm。影响量较大，属于高敏感性参数的范畴。

3.6 二期恒载的敏感性分析

本悬索桥二期恒载主要由桥面铺装，钢-混叠合梁，上下层人行道板，电车轨道等组成，与普通公路悬索桥相比，公轨两用悬索桥二期恒载大，在恒载中，二期恒载的所占比重往往接近甚至超过加劲梁自重所占的比重。本研究中，为了掌握二期恒载的变化对线形计算中各项指标的影响，通过让二期恒载在50%～150%之间变化，探究线形计算中各项指标的变化情况。通过计算对比，二期恒载对各项指标的影响与加劲梁类似，但是相比加劲梁，各项指标的变化速率更大，这也印证了本桥二期恒载的荷载集度大于加劲梁自重的荷载集度。结果如图17～图19所示。

图17 二期恒载变化率与成桥状态主缆内力的关系

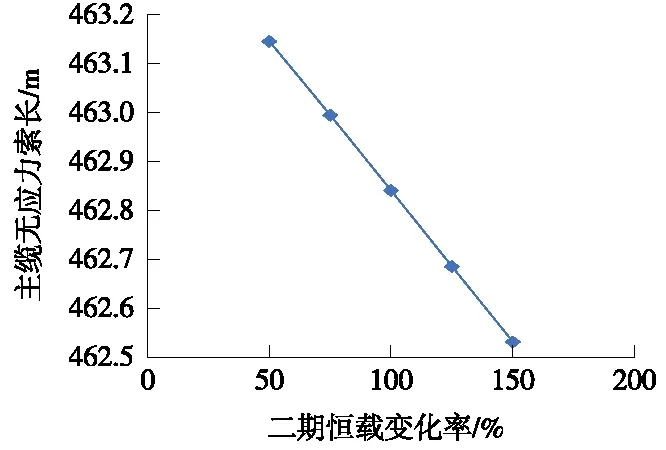
图18 二期恒载变化率与主缆无应力索长的关系

图19 二期恒载与空缆状态主缆高程的关系

由图17可知，随着二期恒载的变化，与加劲梁荷载的影响一样，锚碇张力的增长率最快，水平分力次之，竖向分力最慢。二期恒载每提高5%，锚碇张力提高约4 650 kN，水平分力提高约4 450 kN，竖向分力提高约4 200 kN，与加劲梁自重相比，提高幅度明显，就本桥来说，主缆内力对二期恒载敏感性更高。

由图18可知，主缆无应力索长与二期恒载呈反比，二期恒载每提高5%，主缆无应力索长缩短约31 mm。

由图19可知，二期恒载对空缆高程的影响量相比加劲梁自重来说更大，二期恒载每提高5%，主缆空缆高程提高约115 mm。影响量大，空缆高程对二期恒载的敏感性高。

4 线形影响因素敏感性评价

通过对比研究，针对本项目，对各指标的敏感性进行分类评价，整理得出表8，可为本工程项目的建设工作提供相应指导，也可为类似工程提供参考资料。

表8 公轨两用悬索桥主缆线形敏感性指标评价

注：3分为高度敏感，2分为普通敏感，1分为不敏感。

5 结论

(1)公轨两用悬索桥主缆线形计算对计算方法的敏感性高，分段悬链线法和节线法计算结果十分接近，具有精度高的特点；抛物线法的计算方法简单，但对于本项目的计算精度难以满足工程建设的要求，仅适合初步设计和快速估算时使用。

(2)在进行复核性计算和监控计算时，应选择恰当的计算方法，材料特性、主缆荷载、加劲梁及二期荷载等高敏感性参数，需重点关注并精确输入。

(3)现场监控工作中，温度属于高敏感性参数，应重点监测温度场的变化，并根据测试结果，及时调整架设方案，减小温度对主缆架设质量的影响。

(4)现场监控工作中，为提高主缆线形和成桥线形的监控精度，在架设之前，应通过抽样试验对主缆材料特性参数进行测试，确保参与计算的材料特性参数真实准确；恒载参数方面，应重视荷载统计工作，条件允许，宜采用现场称重的方式获取荷载参数，并将参数及时反馈到监控计算中。