压气机静叶调节机构的柔性多体建模及仿真

张少平，杨 川，张一彬

(中国航发四川燃气涡轮研究院，成都610500)

1 引言

高压压气机的单级或多级静叶调节机构是燃气涡轮发动机防喘的关键部件。其原理是通过调节静叶转角以改变动叶来流攻角，从而避免失速，提高发动机的稳定工作范围[1-2]。理论上，如果所有部件都是刚性的且各运动副都是理想约束，在作动筒移动到一个固定位置时，单级内所有静叶应该转动到一个相同的设计值。但实际上，在考虑尺寸公差、运动副间隙、部件柔性、机匣热变形等众多因素之后，级内所有静叶的转角并不相等，且与设计值存在偏差。单级内各叶片实际转角的一致程度被称为周向一致性，实际转角与理论转角的差异度被称为调节精度。它们是衡量静叶调节机构性能的重要指标，在本文中通过最大偏差角(是指单级叶片偏离设计值的最大角度)来衡量。

分析和优化静叶调节机构的周向一致性和调节精度对扩大涡轮喷气发动机工作范围具有重要意义[3-4]。然而，多级静叶调节机构是个极其复杂的柔性多体系统，动辄含有数百个大小零部件和运动副。要想较精确的分析该系统，理解周向一致性和调节精度的关键设计点，必需借助多体动力学进行动力学仿真分析，进而优化设计[5-8]。

目前利用商业软件如MSC/ADAMS[9]开展动力学仿真建模时，有建模工作量大、计算效率低、长细比较大结构柔性建模可靠度低、难以定位、建模错误等问题。为克服以上问题，赵治华等[10]开发了基于子系统建模的柔性多体动力学软件。其关键是建立最小的子系统模型，然后阵列和组装得到全系统，大幅减少了建模和调试工作量；同时采用几何精确描述的三维空间大变形梁[11]建模联动环，避开了模态综合法的小变形限制。

为研究尺寸公差和运动副间隙、摇臂柔性、联动环柔性、机匣热变形等因素对调节机构周向一致性和调节精度的影响，本文首先利用自研程序建立调节机构的纯刚性模型，并与商业软件ADAMS建立的刚性模型进行定量对比，验证了求解器和模型的正确性。然后通过自研求解器建立多个柔性多体动力学模型，定量分析了以上各因素对静叶调节机构周向一致性和调节精度的影响及影响程度。

2 静叶调节机构建模

图1是一个典型的多级静叶调节机构，单级沿周向有多个静叶，通过摇臂共同连接在一个联动环上；各级联动环通过销钉限制其与机匣之间的距离，并在作动筒的驱动下经曲柄连杆机构连接协同动作。

调节机构工作原理如图2所示，三个曲柄分别于O2、O3和O4点与机匣用转动副连接，作动筒一端O1点球铰在机匣上，另一端A通过平动来转动0级曲柄，同时经1级连杆和2级连杆转动1级和2级曲柄。各级曲柄的转动会带动各级联动环绕机匣轴线旋转。

本次研究流程如图3所示，先装配调节机构三维模型，以此为输入先建立纯刚性模型与小变形摇臂柔性模型；与ADAMS建立模型进行对比，校验自研软件及建立模型的正确性，进而建立考虑尺寸公差、运动副间隙、摇臂柔性、联动环柔性、机匣热变形的多体动力学模型，考察其对偏差角的影响。

基于柔性多体动力学基本理论建立静叶调节机构的仿真模型。在多体动力学里，通常采用第一类拉格朗日方程[12]，全系统最终可构成如下微分代数方程组：

2.1 运动副建模

静叶调节机构中的运动副建模分为理想刚性约束和柔性约束两种。理想刚性约束适用于不考虑运动副间隙、约束弹性的情况，用式(1)中的解析方程C(q)=0描述。本文所用三级静叶调节机构的刚性约束见表1。其余需要考虑运动副间隙、约束弹性的是柔性约束，用考虑两个物体之间的间隙、检测碰撞间隙、计算碰撞力和摩擦力的方式建模，包括叶片轴颈与机匣的连接、摇臂端部与联动环的连接、叶片底部与内环的连接。

2.2 摇臂柔性建模

摇臂采用基于小变形的模态综合法[13]建模。通过有限元软件对摇臂进行模态分析，取前16阶模态作截断近似。网格收敛性分析表明，网格划分到1 mm就可以使频率和模态均收敛。

表1 模型中的理想约束Table 1 Ideal constraint in the entire model

2.3 联动环柔性建模

联动环采用基于大变形的几何精确梁[11]建模。梁的抗弯刚度使用等效原理近似计算。真实的联动环多孔，形状复杂，没有一致的横截形状，通过与有限元对比可以得到其等效抗弯刚度。联动环的变形主要是椭圆变形，故采用图4所示模型进行等效刚度计算：将联动环的左端固定，上下端施加100 N的对向挤压力，测量右端的自由位移，调节梁单元的抗弯刚度，使得在相同边界条件有相同的位移。

2.4 机匣热变形建模

机匣热变形对静叶调节机构的影响十分明显。建模过程中，在有限元软件中分析机匣的热变形[14]，将变形后的机匣作为刚体集成到多体模型中，其结果如图5所示。工作状态下，机匣的温度较高且温度场不均匀，机匣受热膨胀、弯曲后，其上放置静叶片的机匣孔的位置和姿态随之呈周向不均匀改变，从而影响调节机构性能。

机匣孔变形后的姿态使用最小二乘法拟合。如图6所示，假设一个机匣孔上有N个有限元节点，变形前是圆柱形，变形后的位置为点集{(xi,yi,zi)|1≤i≤N}，现需要确定圆柱位置中心(x0,y0,z0)和圆柱轴向单位向量(n1,n2,n3)。圆柱位置中心可由算数平均得到，即：

圆柱轴向单位向量则由最小二乘法拟合：根据最小二乘法原理，确定参数n=(n1,n2,n3)以及由这些参数确定的圆柱内表面S1(S1的半径使用未变形时的半径R)，使得点集{(xi,yi,zi)|1≤i≤N}到S1的距离的平方和最小，公式为

式中：ri=(xi,yi,zi)-(x0,y0,z0)。由于(n1,n2,n3)并不独立，而是满足归一化方程f=0，其中

令F=D+λf，则由带约束乘子的第一类拉格朗日方程可以得到求解拟合轴向参数n的方程组为：

用牛顿迭代法求解此方程，将迭代误差设置为1.0×10-8，迭代结束后就能得到变形后的叶片孔内表面圆柱面的拟合轴向单位向量。

2.5 其他部件的热变形建模

在考虑机匣热变形时，为使模型协调，必须考虑联动环、连杆、曲柄和叶片的热变形。这几个零件受热后发生热膨胀，杆件长度发生变化，先使用有限元软件进行分析，再将膨胀量以公差的方式赋给各部件。连杆是零级曲柄连接一级曲柄和二级曲柄的部件，其受热膨胀后长度伸长，使得一级、二级产生热效静角度差。通过分析热效静角度差，可指导常温条件下的材料针对工作状态(受热)下的连杆尺寸设计。曲柄的膨胀变形与连杆热变形的效果相似。

2.6 受热模型的积分预处理

用受热变形后的部件替换常温部件时，许多原来满足的约束将出现比较严重的约束违反现象。因此对受热模型需要做积分预处理才能完成仿真。如图7所示，在初始时刻(-2 s到0 s时间段里)改变约束违反处的刚度和阻尼，防止约束违反严重造成积分失败，使得-2 s到-1 s内刚度只有0.1%，阻尼为10倍；-1 s到0 s内，逐渐恢复刚度和阻尼到正常值。

3 模型校验

因多体仿真软件ADAMS在刚性模型仿真及小变形柔性仿真方面较成熟，其应用得到广泛肯定。用自研程序和ADAMS软件分别建立纯刚性和考虑摇臂小变形两个动力学计算模型，并比较两套程序的计算结果，以此来验证自研软件及建模的正确性。

计算条件为：零级静叶驱动角度范围为-20°～20°，此时一级静叶对应-15°～15°，二级静叶对应-12°～12°。将静叶在允许范围内来回驱动一周。为了数值模拟的需要，将驱动曲线设计成式(6)所示的3次光滑曲线，如图8所示。

在纯刚性假设下所有静叶的转角一致，自研程序与商业软件的计算结果对比如表2所示，考虑摇臂柔性后的计算结果对比如表3所示。可见两个程序在计算精度上无显著差别，以ADAMS计算结果作为参考值，自研程序所得结果与参考值最大相差不到1%，说明自研程序及建立的模型均可接受。

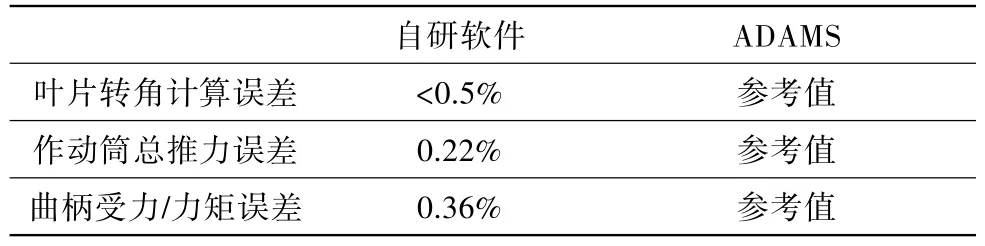
表2 自研程序与商业软件在纯刚体模型上的结果比较Table 2 Comparison between in-house program and ADAMS for rigid model

表3 自研程序与商业软件在柔性摇臂模型上的结果比较Table 3 Comparison results of the in-house code and ADAMS on models of flexible rockers

4 仿真结果

利用自研程序建立多个模型，其驱动与程序校验时一致。通过对比，逐个研究尺寸公差、运动副间隙、摇臂柔性、联动环柔性和机匣热变形对静叶调节机构周向一致性和调节精度的影响程度。为尽可能真实模拟使用工况，在后继建立的模型中均考虑气动力和力矩，如图9所示。

4.1 尺寸公差与运动副间隙的影响

按2.1中论述的建模方法建立3个纯刚体假设的模型：一是所有部件的尺寸均为设计值；二是仅考虑尺寸公差，三级连杆尺寸公差均设为1.0 mm；三是无尺寸公差仅考虑运动副间隙，间隙值依据设计分布在0.1～0.2 mm之间。三个模型的计算结果如表4所示：纯刚性模型的最大偏差角仅为0.05°，其值非零的原因是因为部分约束采用柔性约束建模，仅有尺寸公差对最大偏差角的改变不大；仅有运动副间隙的偏差模型的最大偏差角为0.74°。与后继研究对比可见，尺寸公差的影响可忽略，运动副间隙影响略大。

4.2 联动环与摇臂柔性的影响

将纯刚体模型、仅考虑联动环柔性模型、仅考虑摇臂柔性模型以及同时考虑联动环和摇臂柔性模型共4个模型的三级叶片最大偏差角结果进行对比，如表5所示。结果表明，联动环柔性与摇臂柔性相互耦合、相互作用，仅考虑联动环柔性或仅考虑摇臂柔性所得的偏差角，均远小于同时考虑联动环和摇臂柔性的偏差角。

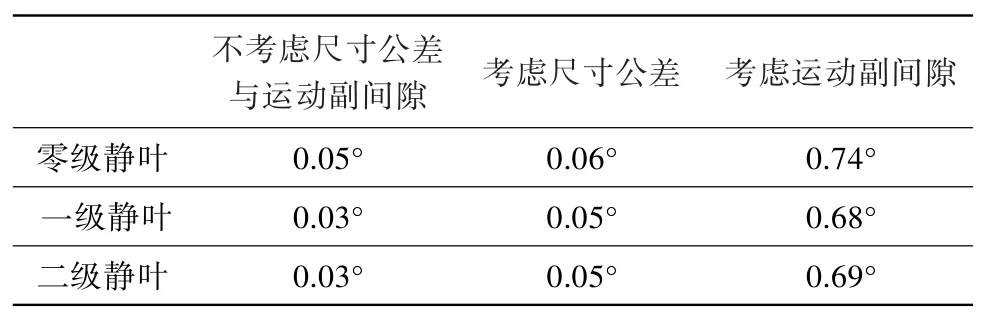
表4 尺寸公差和运动副间隙对最大偏差角的影响Table 4 Effect of lengths error and joints clearance on maximum deflection angles

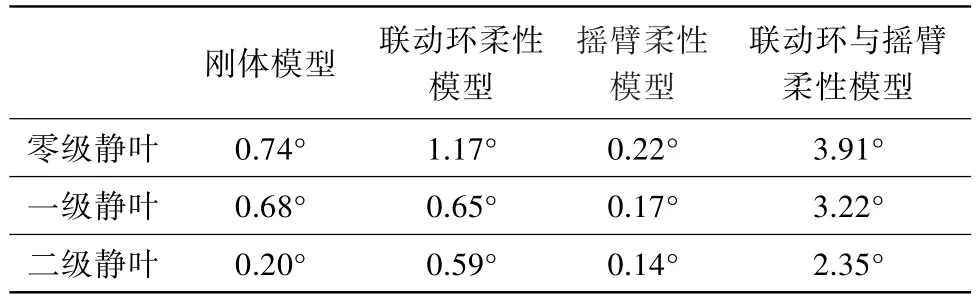
表5 联动环与摇臂柔性对最大偏差角的影响Table 5 Effects of flexibility of linkage and rockers on maximum deflection angles

分析认为，联动环柔性与摇臂柔性耦合放大偏差角的机理如下：联动环驱动被动静叶克服来自机匣和内环的摩擦力运动，反作用力沿联动环切线方向并使得联动环发生变形，曲柄处边界条件以及旋转对称的分布载荷决定了变形是类椭圆的；联动环的类椭圆变形导致摇臂同时产生沿切向的旋转和沿径向的变形，摇臂变形的反作用力沿联动环径向抑制联动环变形，如图10所示。如果不考虑联动环或摇臂中某一个的柔性，则均会导致上面的耦合回路中有一部分得到了显著抑制，其结果比考虑耦合的偏差小。所以要提高调节精度，需同时增大联动环和摇臂厚度方向的抗弯刚度，而不能仅增加单类部件的刚度。

4.3 受热模型仿真结果与分析

在考虑联动环和摇臂柔性的同时，建立机匣常温模型和考虑机匣热变形的模型，两个模型的仿真结果对比如图11所示。结果表明，在初始时刻，机匣的热变形造成了一个角度漂移，零级静叶约0.59°，一级静叶约 1.04°，二级静叶约 1.14°，并造成最大0.60°的角度分散。由于初始静偏差是单方向的，对后续一个来回的驱动过程造成的影响各不相同：在驱动的前半段，机匣热变形导致的初始角度漂移减小了最大偏差角；在驱动的后半段，机匣热变形导致的初始角度漂移增大了最大偏差角。

4.4 各因素影响汇总

运动副间隙、联动环和摇臂柔性以及热变形对最大偏差角的影响如图12所示。对比可见，纯刚性无公差无间隙模型偏差角可忽略；运动副间隙的影响没有柔性大；而同时考虑柔性和热变形后，因热变形导致三级联动环所在位置的变形不一致，会显著改变偏差角分布，比如仅考虑柔性最大偏差角为零级最大、二级最小，考虑热变形后最大偏差角为零级最小、二级最大。

5 结论

建立了多级静叶调节机构的柔性多体动力学模型，在验证模型正确性的基础上，定量分析了尺寸公差、运动副间隙、摇臂柔性、联动环柔性、机匣热变形等因素对压气机静叶调节机构周向一致性和调节精度的影响程度，得出：

(1)尺寸公差和运动副间隙的影响小，在调节机构优化时，可暂不考虑加严公差或减小运动副间隙。

(2)联动环和摇臂的柔性存在显著的耦合放大效应，且对周向一致性有显著影响，在调节机构优化时应同时增大两者的刚度。

(3)机匣热变形对周向一致性和调节精度有显著影响，在热设计时应尽量减小温差，或通过结构设计使机匣变形协调一致，减小变形对调节精度及调节角度一致性的影响。