ARIMA模型在某市刑事类警情预测中的应用

宋兆铭，严 理，曾欣欣

（1.四川警察学院 四川泸州 646000；2.内江市公安局 四川内江 641100）

随着现代数据分析手段的不断更新与进步，公安情报的定量研究也在不断地发展。相关研究表明，若持续跟踪某一现象，可能会获得更多的信息。时间序列是按时间次序排列的随机变量序列[1]。对时间序列进行观察、研究，找寻它变化发展的规律，预测它将来的走势就是时间序列分析[2]。刘剑宇等（2009）采用移动平均法对某地1988-2005年吸毒人数时间序列数据进行建模与预测，结果表明，当序列数据不快速增长或下降且不存在季节性因素时，移动平均法能有效地消除预测中的随机波动，能对未来吸毒人数的变化趋势作出较为准确的判断预测[3]。张姝等（2009）采用多项式曲线拟合的方法对1991-2006年全国吸毒人数时间序列数据进行建模与预测，结果表明，我国吸毒人数的发展趋势是不断增长的；通过预测数据与实际数据的对比检验，在不考虑观测数据自身的误差以及与模型状态变量之间的联系下，多项式曲线拟合全国吸毒人数时间序列的预测结果较为准确[4]。刘蕾等（2009）采用多项式曲线法对1986—2007年我国口岸交通运输工具出入境总数时间序列数据进行建模与预测，研究结果表明其量化分析结果可直接服务于警务决策，能更好地发挥情报工作的经济效益和社会效益[5]。陈春东等（2012）采用ARIMA模型对A市2004年8月至2007年8月盗窃案事件的历史数据进行分析，认为ARIMA模型对盗窃案件的短期预测具有较好的效果，建议在实际应用中应进一步推广[6]。陈鹏等（2015）分别采用ARIMA模型和指数平滑模型分别对廊坊市2012年110警情数据进行建模对比分析，结果认为ARIMA模型相对于指数平滑模型能较好地反映出治安案件变化的短期趋势和随机波动性特征，更适用于警情分析的短期预测[7]。综上，当前研究者都深度使用了时间序列分析的方法来预测各类公安情报信息的趋势，并取得了较好的效果，弥补了在公安情报分析实际工作中主要依赖经验分析的不足。

刑事类警情数量的高低是衡量社会治安形势总体分析评价的重要标准之一[7]。虽然刑事类警情具有随机性极强的特点[6]，但同时上述前人研究也表明科学定量地分析，是可以制定相应的警情预警机制与社会治理策略，从而达到最佳的社会治理效益。因此，本研究在依据刑事类警情特点以及前人相关研究的基础上，利用2015年1月至2017年12月某市刑事类警情数据[8]，探讨ARIMA模型在刑事类警情建模和预测中的应用，以期能探究某市刑事类警情的变化规律，并在此基础上合理地优化警力配置，调整警力部署尤其是警力的投量，努力使警力覆盖的时段与刑事类警情高发的时段相吻合，从而提高与违法犯罪的碰撞几率，实现警务效能的最大化，并为探究“大数据驱动下的预测警务创新实践”[9]提供实证方法。

一、ARIMA模型概述

（一）ARIMA模型概念

ARIMA模型全称为求和自回归移动平均（autoregressive integrated moving average）模型，简记为ARIMA(p，d q)模型[2]。ARIMA模型是由Box和Jenkins于70年代初提出的时间序列预测方法，所以又称Box-Jenkins模型[10]。ARIMA模型以时间序列的自相关分析为基础，将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。因此，ARIMA模型在预测过程中不仅考虑了某一现象在时间序列上的依存性，又考虑了随机波动的干扰性，对于某一现象运行短期趋势的预测准确率较高，是应用广泛的时间序列预测方法之一[6][7]。

（二）ARIMA模型过程

ARIMA模型根据原序列是否平稳以及回归中所含部分的不同，又可细分为：p阶自回归模型（AR（p））[2]、q阶移动平均模型（MA（q））[2]、自回归移动平均模型（ARMA（p，q））[2]以及ARIMA（p，d，q）过程四大类[2]。

1 p阶自回归模型（AR（p））

称平稳序列服从于AR（p）模型，即：在一个p阶自回归模型中，序列中的每一个值都可以用它之前p个值的线性组合来表示，模型表达式如下：

其中，xt是时序中的任一观测值，δ是序列的均值，Φ是权重随机扰动，μt是白噪声序列 （均值为0，同方差，无自相关）；AR（p）平稳的充要条件是特征根都在单位圆之外（均值、方差和协方差都是有限的常数）。

2 q阶移动平均模型（MA（q））

称平稳序列服从于MA（q）模型，即：在一个q阶移动平均模型中，时序中的每个值都可以用之前的q个残差的线性组合来表示，模型表达式如下：

其中，μt是白噪声过程；MA（q）是由本身μt和q个μt的滞后项加权平均构造出来的，因此它是平稳的，其平稳性与系数无关。但是，经常需要将AR模型表示为MA模型，反过来也一样，这称为可逆性。MA（q）可逆性（用自回归序列表示μt）：

MA（q）可逆条件为θ（L）每个特征根绝对值大于1，即全部特征根在单位圆之外。

3自回归移动平均模型（ARMA（p，q））

AR（p）与MA（q）两种方法的混合即ARMA(p，q)模型，称平稳序列服从于ARMA(p，q)模型，同时序列中的每个观测值用过去的p个观测值和q个残差的线性组合来表示，模型表达式如下：

4求和自回归移动平均模型ARIMA（p，d，q）

ARIMA(p，d，q)模型意味着时序被差分了d次，且序列中的每个观测值都是用过去的p个观测值和q个残差的线性组合表示的，预测是“无误差的”或完整的，来实现最终的预测。

差分算子表达式如下：

对d阶单整序列表达式如下：

则是平稳序列，可对建立 ARMA(p，q)模型，所得到的模型称为-ARIMA（p，d，q），由此转化为AMRA模型。

综上公式可以看出，ARIMA模型实际上就是差分运算与ARMA模型的组合[2]146，即：可以通俗地理解为ARMA模型升级版，由于序列不平稳，差分后成了ARMA模型。这是因为任何一个时间序列的波动都可以被视为同时受到了确定性因素和随机性因素的综合作用。

（三）ARIMA建模程序

ARIMA建模程序如下：

1.获取被观测数据，画出序列的时序图，观察序列是否平稳。

2.若平稳序列的偏相关函数是截尾的，而自相关函数是拖尾的，可断定序列适合AR（p）模型；若平稳序列的偏相关函数是拖尾的，而自相关函数是截尾的，则可断定序列适合MA（q）模型；若平稳序列的偏相关函数和自相关函数均是拖尾的，则序列适合ARMA（p，q）模型；若为非平稳序列要先进行d阶差分运算后化为平稳序列，则序列适合ARIMA(p，d，q)模型[11]。

3.对得到的平稳时间序列分别求其自相关系数（ACF）和偏自相关系数（pACF），在初始估计中选择尽可能少的参数前提下，通过对ACF图和pACF图的分析得到最佳的识别模型参数（阶层p和阶数q），从而得到ARIMA模型。

4.模型诊断，证实所得模型与所观察的数据特征是否相符，即：残差序列是否为白噪声序列，若是则可用来预测，若不是则需重复第3步过程，进一步改进模型。

5.利用已通过检验的模型进行预测分析。鉴于上述分析过程，可以构建ARIMA建模流程图[12]，如图1所示。

图1 ARIMA建模程序图

二、实证分析

在现实中，由于刑事类警情的发生存在各类的随机性因素，因此建立一个完美的时间序列模型是比较困难的，上述ARIMA建模思路可以提供一个较为有效的实现路径。本研究通过对某市2015年1月至2017年12月刑事类警情数据进行搜集，结合R软件tseries和forecast程序包[13]，依据上述建模过程对其进行建模分析，具体如下：

（一）时序图和平稳化处理

从图2可以看出2015—2018年某市刑事类警情整上呈下降的趋势，并且自相关图里自相关系数没有快速的减为0（一般认为自相关系数低于2倍标准差即图中蓝色虚线一下时即为0）[2]，而是呈现出拖尾的特征，故判断序列为非平稳序列，应考虑差分转化为平稳序列。

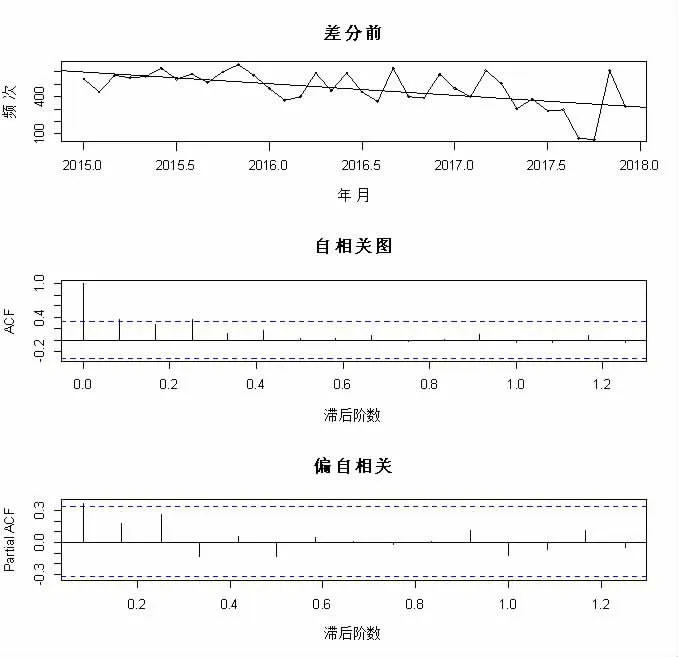
图2 某市刑事类警情时序与自相关、偏自相关图

从图3可以看到，1阶差分以后序列变为平稳序列，且自相关图显示自相关系数在滞后1阶后就快速的减为0[2]。同时，使用ADF单位根检验，结果显示p-value=0.01163，进一步表明序列经一阶差分后已经实现平稳。

图3 差分后某市刑事类警情时序与自相关图

（二）模型的定阶及参数估计

采用auto.arima()函数实现最优ARIMA模型的自动建模[12]。建模结果如图3：

图4 ARIMA模型的自动建模结果图

从图4输出结果可以看出，auto.arima()函数自动选取的最优模型是ARIMA(0，0，0)(0，1，1)[12]模型，模型估计表达式为：

（三）模型检验

为证实所得模型确实与所观察到的数据特征相符，ARIMA模型参数检验包括两个检验：（1）参数的显著性和残差的正态性检验。参数的显著性检验是用估计出的系数除以其的标准差(se)得到的商与T统计量5%的临界值（1.96）比较，商的绝对值大于1.96，则拒绝原假设，认为系数显著的不为0，否则认为系数不显著。画出残差的qq图即可判断残差的正态性，即：qq图中残差基本完全落在45°线上即为符合正态性假设。（2）白噪声检验。白噪声检验也称为残差的无关性检验，指此序列即都是随机扰动，无法进行预测和使用，即：残差（=估计值-真实值）应为不相关的序列[2]。常用LB统计量来检验残差（q=n(n+2)∑(ρ/(n-k))）。

图5 ARIMA自动建模残差qq图

从图5画出的qq图（点大多落在图中的直线上）和LB检验（p-value=0.9943）的结果来看，残差符合正态性假设且不相关，模型拟合数据比较充分，可以用来进行下一步预测。

（四）预测

通过forecast()函数，使用最优模型ARIMA(0，0，0)(0，1，1)[12]做预测，并依据真实值来进一步判定模型的预测效果。

图6 ARIMA最优模型预测图

由于某市公安局官网数据的更新，本研究仅对2018年1月的刑事类警情预测值与真实值作比较。其中，刑事类警情预测值为290次，真实值为315次，落在了95%的置信区间之间，说明预测值在一个合理的范围之内（图6）。

三、讨论与分析

刑事犯罪随着经济社会的发展而增长，但同时刑事类警情数量与群众安全感满意度也密切相关。近年来，某市公安局紧紧围绕打造“全国平安示范区目标”，全面加强组织领导，集中力量攻坚克难，推动了一系列 “平安某市”建设的举措。主要有：（1）强化技防建设。加强重点场所部位技术防范，扩大技防覆盖面，2015年实现城乡“天网”全覆盖，城乡“天网”监控点位达4000多个，加上社会力量视频监控资源，全市视频监控探头达29000多个，并实现重点场所视频监控探头与公安监控中心联网运行。（2）推进网格化服务管理，推进基础工作信息化。坚持“全警采集、全警录入”原则，加强对接处警、巡逻盘查、案事件、“一标三实”和实名制信息等基础工作的采集，全面加快了市级平台建设和农村网格覆盖速度并实现全覆盖。落实实有人口管理，特别是重点人员“人来24小时内登记、人走及时注销”要求，着力提升发现和预防犯罪能力。（3）创新反恐防暴及街面治安防控新机制[14]。把全市城区划分为25个巡区，确定201条必巡线、181个必巡点和88个巡逻车辆经常性停靠点，设置159个巡更点，24小时屯警街面，且由指挥中心直接调度扁平化指挥[9]，构建了一警多能、诸警联动，点、线、圈紧密协同的立体化街面防控新机制，实现了一级接处警。同时，虽然刑事类警情具有随机性，且从图1某市2015-2018刑事类警情的变化看也确实存在一定的波动，但从其整体呈下降的趋势来看，是可以证明某市公安局上述措施确实提高了“见警率”“管事率”，有力地维护了某市社会政治稳定和治安大局平稳。

四、结果结论

综上所述，可以得到以下结果结论：

（一）时间序列ARIMA模型算法拟合度较高，选取的最优模型ARIMA(0，0，0)(0，1，1)[12]能较好地拟合既往时间段某市刑事类警情的变化；对某市2018年1月的刑事类警情实证预测表明，其预测值与真实值的拟合度在短期内较高（预测值290次，真实值315次），预测偏差较小（95%的置信区间），其预测趋势与某市刑事类警情的实际变化趋势一致。这表明对刑事类警情的分析，ARIMA模型有效，可以应用于刑事类警情的情报分析与预测。

（二）某市2015-2018刑事类警情整体上呈下降趋势。这可能与近年来某市公安局紧紧围绕打造“全国平安示范区目标”，推动了一系列 “平安某市”建设的举措有关。

（三）尽管ARIMA模型对于理解、预测刑事类警情是有效的，但是ARIMA模型都用到了向外推断的思想，即：它假定未来的条件与现在的条件是相似的，比如：它依据2017年的刑事类警情就认为2018年及以后的刑事类警情会与2017年一样稳定，但事实并不是这样，诸如警务活动主体、对象和环境的情形与变化等都可能改变序列中的趋势和模式。因此，ARIMA模型是利用历史数据来挖掘有用的信息来预测未来的趋势，是一种直观分析，如果时间跨度越大，其不确定性就会越大，仅适合短期预测使用。