考虑渗流时滞及参数不确定性的土坝坝坡失稳概率分析

徐镇凯，蔡 磊，魏博文，王 锋

(南昌大学建筑工程学院，江西南昌330031)

坝坡稳定问题是土石坝设计及运行管理关注的重点内容之一。由于渗流问题具有复杂性，其影响因素繁多，水位、土体参数等都是影响其安全系数大小的因素。国内外学者针对坝前水位的升降引起坝体内部渗流场发生变化，进而诱发的坝坡稳定问题进行了大量研究，郑颖人等[1]、时卫民等[2]研究了由水位下降导致的浸润线变化为基础引起边坡失稳的影响；唐辉明等[3]基于非饱和土强度理论，研究了库水位在不同下降速率下的土石坝坝坡稳定性，得出稳定性系数极小值的出现与水位下降速度密切相关；Terzaghi[4]就库水位变化时对滑坡体稳定性的影响进行了专门分析，并指出库水位骤降坡脚会出现渗透变形的情况；文献[5- 6]通过建立耦合模型分析库水位快速下降引起的滑坡失稳，同时分析对比了数值模拟结果与现场检测数据。赵瑞欣等[7]通过分析三峡库区凉水井滑坡，对水位变化速率分析，得出在同一渗透系数的前提下，水位骤降的风险最大。

综上所述，库水位变化对浸润线变化、土体强度的影响是一个复杂的过程，其导致土石坝坝坡土体经历饱和-非饱和的循环转化，最终影响坝坡。现有研究中，蒙特卡洛法、一阶矩和二阶矩等方法被广泛应用于结构可靠性分析中[8- 9]。其中，蒙特卡洛法虽模拟计算精度高，但其计算量巨大；而一阶矩法和二阶矩法计算精度亟待提升。坝坡稳定分析多基于极限平衡法和极限分析法[10]进行数值模拟，再结合蒙特卡洛模拟法计算结果，分析过程繁琐，限制了其在工程中的应用。

本文在GEOSTUDIO软件建立有限元分析模型的基础上，建立了考虑土石坝上游水位骤降的坝坡稳定可靠度模型。通过对坝体进行应力分析，结合Kriging方法，推导了土石坝坝坡稳定安全系数解析式与相应可靠度功能函数，分析了土石坝坝坡稳定性。工程实例分析表明，本文所建模型计算精度高、收敛速度快、计算分析简便，可为土石坝健康服役提供理论依据与决策支持。

1 土石坝坝坡失稳概率的分析方法

1.1 安全系数解析式

实际工程中，结构正常使用极限状态中抗力效应R和荷载效应S的功能函数关系式为

Z=g(R，S)=R-S

当坝坡处于极限状态时，R-S=0。国内学者常结合安全系数和可靠度理论建立可靠度分析功能函数对坝坡进行稳定可靠性分析[11]，基于稳定安全系数的可靠度分析功能函数表达式为

Z=Fs-1

式中，Z为功能函数；Fs为坝坡稳定安全系数。

采用简化毕肖普方法计算坝坡的抗滑稳定安全系数，即

式中，c′i和φ′i分别为土的有效黏聚力和内摩擦角；Wi和bi分别为土条的质量和宽度；αi为土条滑面的倾角。

1.2 坝体内部渗流的时滞特性

库水位对土石坝渗流性态的影响是一个逐变过程，在水位变化情况下，引入水位滞后影响函数来反映库水位时滞作用。假设Hi(i=1，2，3…，n)为当前水位，Hd为能产生与上述水位等效渗流性态的等效水位

Hd=y(H1，H2，…Hi，…Hn，

w1，w2，…wi，…wn，)

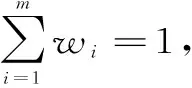
由于渗流效应是由库水位引起的时变连续函数，故等效水位也为时变连续函数[12]。设相应的影响程度分布密度函数为w(t)。根据大量的统计分析发现w(t)的一般规律接近正态分布(μ，σ2)，因此w(t)可表示为

式中，x1为库水位滞后时间；x2为库水位影响时间；A为调整参数。在一定时间范围内，x1，x2为定值，A常视为常数。可得

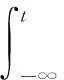
设在t=t0时刻其对应水位的影响程度分布密度函数为w(t)，对应等效水位为Hd，则

式中，H(t)为t时刻的水位。上式结合统计学理论即可求出x1，x2。

由于水库长期蓄水，库水位骤降时坝体内的孔隙水不能及时从土体内排出，坝前水位的突然下降，导致了坝前水压突然减小。随着时间变化，坝体水逐渐流失，致使坝体浮托力减小，同时孔隙水压的增大，导致土料间的有效应力的降低，抗剪强度随之降低。上述两方面影响因素协同驱动引起土体边坡的稳定性发生变异，导致坝坡失稳破坏。

2 基于Kriging模型的可靠性功能函数

Kriging方法[13- 15]最早由南非学者Krige提出并应用于地质统计学研究。Romero等[16]分析对比结合了拉丁超立方抽样的Kriging方法的结构可靠度计算与其他插值技术方法的可靠度计算。我国学者张崎等[17]提出了一种用于结构可靠度计算且具有较高计算效率的基于kriging模型的重要抽样方法。佟操等[18]通过结合蒙特卡洛法和Kriging方法提出了一种有效提高可靠度计算效率及其精度的可靠度主动学习算法。Kriging方法是一种半参数化模拟方法，其表达式为

式中，f(x)T=[f1(x)，f2(x)，…，fn(x)]，为回归模型；β=[β1，β2，...，βn]T，为回归系数；z(x)为随机误差。Kriging模型与响应面法最主要的不同点在于z(x)是一个随机过程，服从正态分布N(0，σ2)，z(x)的协方差矩阵为

cov [z(w)，z(x)]=σ2R(θ，w，x)

式中，R(θ，w，x)是以θ为参数的相关模型，其中w，x∈Rn。R(θ，w，x)为任何两个样本点w和x的空间相关函数，它对模拟的精确程度起决定性作用。

线性函数、高斯函数、指数函数以及广义指函数等都应用于Kriging方法的建模过程，其中使用高斯函数相关函数的计算效果最佳[19]。本文采用高斯函数，则有

假定随机抽样m个坐标点组成的矩阵为S=[s1，s2，…，sm]T；Y=[y1，y2，…，ym]T，为相应坐标点的响应值矩阵。定义R=(Rij)m×m为S中坐标点的相关矩阵，其中Rij=R(θ，si，sj)，(i，j=1，2，…，m)。构造m维权系数向量，c=[c1，c2，…，cm]T，根据响应值yi(i=1，2，…，m)的线性加权叠加来预测待测点x的响应值，可得

要建立最优Kriging模型即将最优Kriging建模过程转换为某一非线性无约束优化问题的求解过程，通过求解上述优化问题，求得参数θk后，即可建立最优Kriging模型。

3 可靠度分析流程

土石坝有限元模型的建立涉及有限元应力分布，土石坝坝坡安全系数FS同坝体材料物理参数之间的关系一般为隐式函数关系。利用Kriging方法并结合软件GEOSTUDIO对土石坝坝坡隐式功能函数进行拟合，实现对土石坝坝坡稳定可靠度的分析，其计算流程图如图1所示。

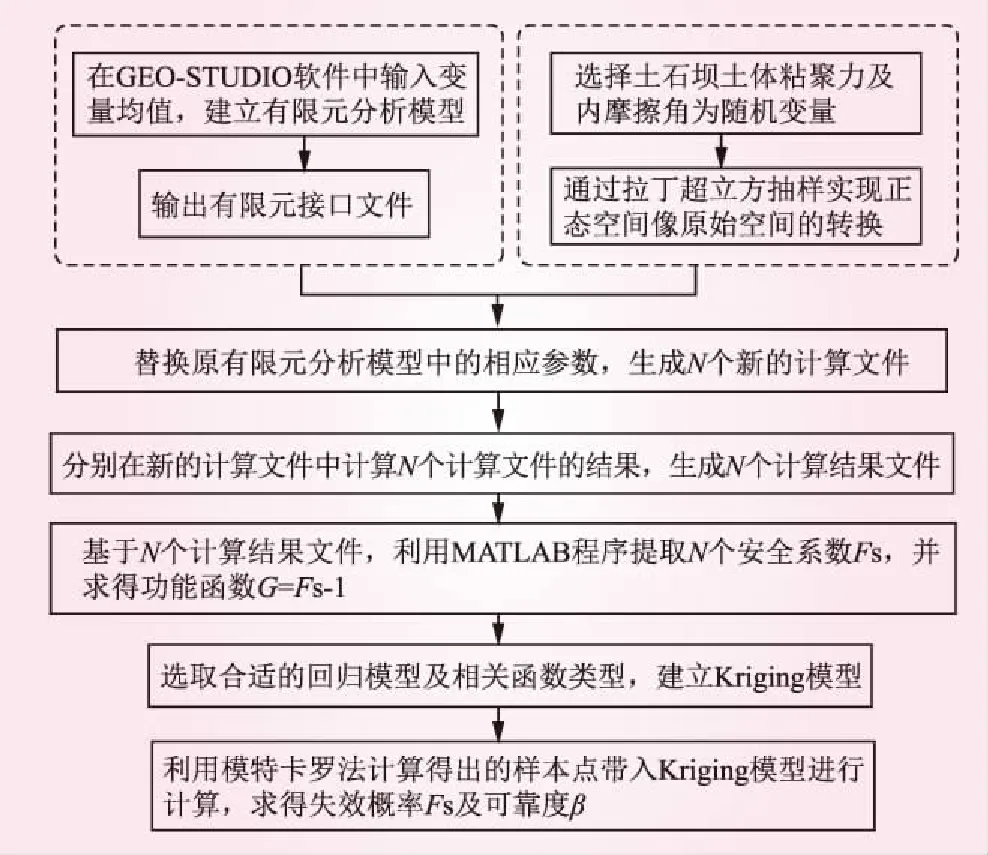
图1 基于Kriging模型的坝坡稳定可靠度分析流程

为确定建立Kriging模型的最佳样本点数，分别建立不同样本点数模型，记录Morgenstern-Price法(M-P法)并与2万次蒙塔卡洛法(MC法)计算结果相对比，见表1。易知当样本点数为40时，相对误差最小，故本文选取的样本点数为40。

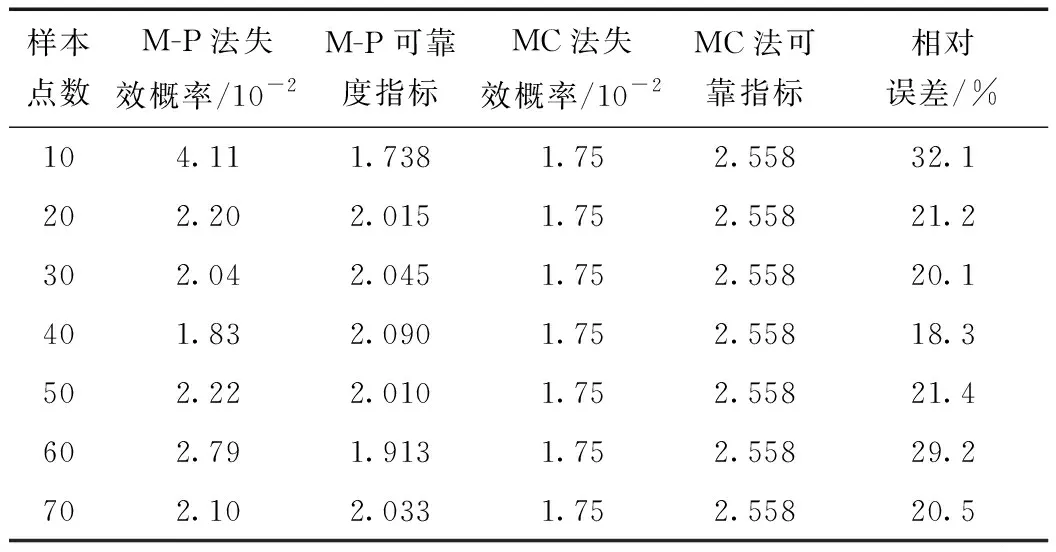
表1 M-P法与MC法对比

4 案例考证

土石坝土体的主要参数包括粘聚力c、容重γ、内摩擦角φ。其中，c、φ对土石坝边坡稳定分析的影响程度较大，γ影响程度较小，故本文只考虑c、φ的变异影响。库区水位骤降是边坡稳定性最不利的情况，极易导致灾害的发生。据统计，在大坝事故中有1/4是由于土石坝滑坡导致的溃坝事故，就滑坡位置而言，上游滑坡导致的溃坝数量远低于下游滑坡[20]，但在实际工程中必须防止因水位骤降引起的滑坡事故发生，本文选取土石坝上游水位骤降情况建立有限元模型。

4.1 模型的建立

某均质土石坝，坝高50 m，坝基标高50 m，坝基影响深度与坝高相等，坝基宽486 m，坝顶宽10 m。大坝运行期正常蓄水位h1=98 m，死水位h2=86 m，大坝下游水位h3=52 m。马道位于下游坝坡高程70 m处，宽1 m，上游坝坡坡比1∶m=1∶3，下游坝坡坡比均为1∶n=1∶2.5，下游设排水棱体。

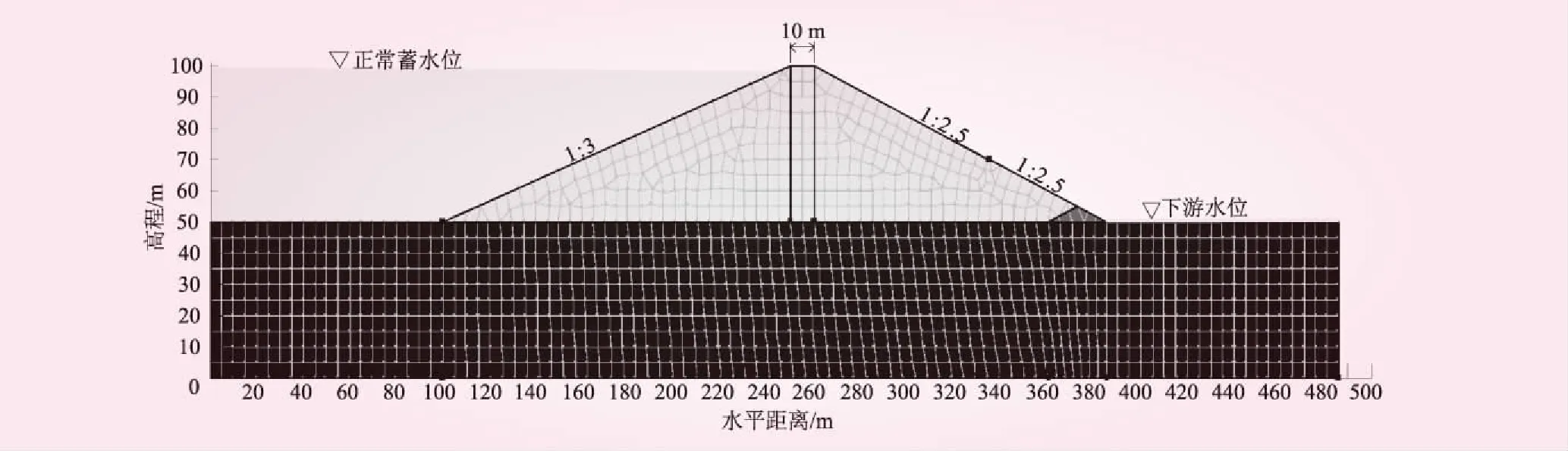
图4 土石坝有限元模型

4.2 材料参数的选取

土石坝有限元模型建立的过程中涉及坝体土、排水棱体材料及坝基土三种材料，其中，坝体土渗透系数k为6.50×10-7m/s、容重γ为20.20 kg/m3；排水棱体渗透系数k为16.40×10-6m/s、容重γ为19.00 kg/m3；坝基土渗透系数k为3.04×10-7m/s、容重γ为22.10 kg/m3。参数统计特性见表2，分布类型均为对数正态分布。

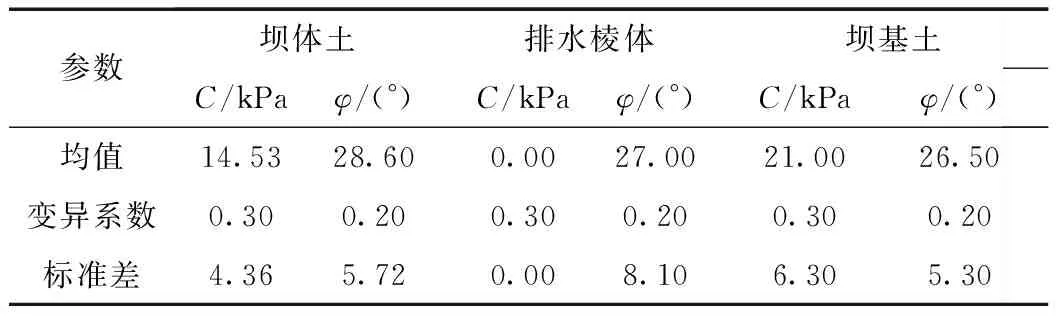
表2 材料参数统计特性

三种材料的体积含水量函数及渗透系数函数均采用Van Genuchten模型估算法进行估算，坝体土体积含水量函数及渗透系数函数关系曲线见图2、3。

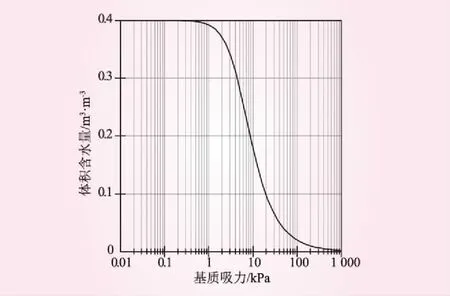
图2 坝体土体积含水量函数

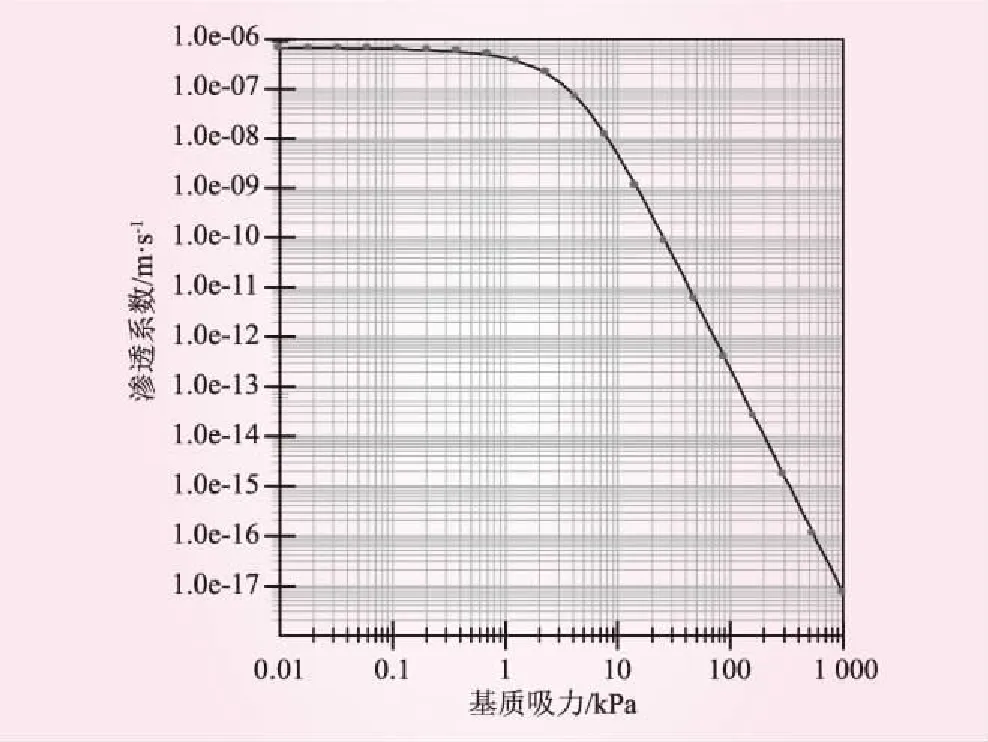
图3 坝体土渗透系数函数

土石坝几何模型参数所建模型见图4，土石坝进行有限元网格的划分时主要采用三角形及四边形网格，横断面共划分单元数1 288个，节点数1 385个。

4.3 计算结果分析

图5给出了水位骤降开始前和结束后一段时间后的孔隙水压力分布曲线。由图5可以看出，在水位下降过程中，由于坝体水的排出，涂料陷落压实，孔隙水压有一个短暂的上升，随后坝体水排出，孔隙水压迅速下降，土体由饱和状态逐渐变为非饱和状态，上游坝面负压区范围变大，正压变小。

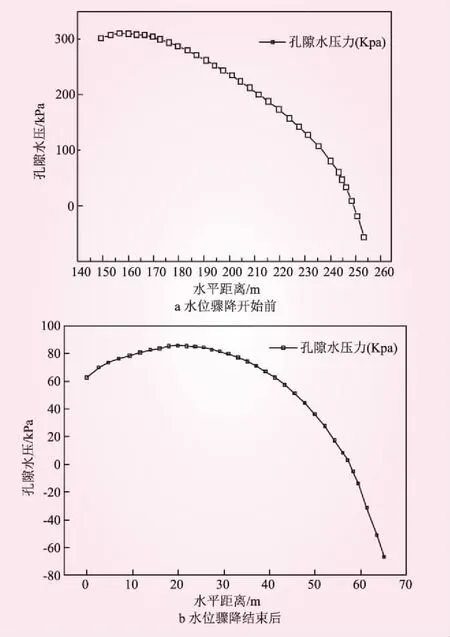
图5 水位骤降前后孔隙水压分布

利用MATLAB程序计算坝坡可靠度随时间变化趋势如图6所示。由图6分析可知：在水位骤降过程中，坝坡可靠度是时刻变化的，由于水位的变化，上游坝坡失效概率逐渐增大，可靠度逐渐降低，由于计算时间步长呈指数变化，导致计算结果形成突变，总体而言，水位骤降导致坝坡失稳，可靠度逐渐降低，随着时间变化，孔隙水的排出，可靠度有所增大，整体呈现出先减小后稍增大的趋势，但变化不大，趋于稳定。在采用Kriging法对上游游坝坡稳定可靠度进行分析时，上游水位的下降，坝坡失效概率逐渐增大，相应的可靠度指标逐渐减小，在水位下降过程中，存在最危险水位，但该水位难以确定，当水位下降至该水位时，失效概率最大，相应的可靠度指标最小。

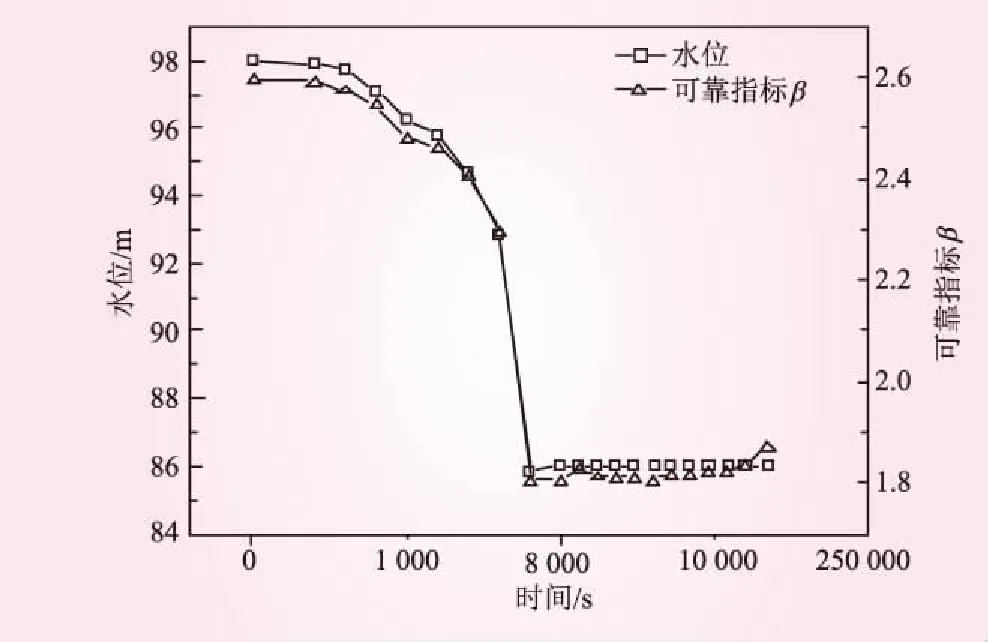
图6 可靠度随时间变化曲线

为验证Kriging模型计算结果的准确性，分别采用已建Kriging模型及蒙特卡洛(MC)法分析在稳定渗流条件下，上游正常蓄水位、下游无水情况下的饱和—非饱和土石坝下游坝坡稳定可靠度问题，其计算结果见表2。其中，MC法抽样次数为10万次。由表2中的计算结果可知，计算结果相对误差为0.12%，该计算工况下的相对误差较小，验证了本文提出的利用Kriging方法计算可靠度结果精度满足工程要求。

表3 坝坡稳定可靠度分析结果

5 结 论

(1)研究了土石坝在水位骤降情况下，上游水位时滞效应下的土坝渗流变化规律，得出了在水位骤降情况下等效水位的计算公式。分析得出体积含水量是关于孔隙水压力的函数，在水位下降过程中，土体含水量随时间逐渐变化，可靠度指标随时间逐渐变化。

(2)本文利用Kriging方法对土石坝坝坡稳定可靠度问题进行分析求解，Kriging方法拥有较为成熟的迭代规则，只需进行较少运算便可获得较为精确的结果。与蒙特卡洛模拟法相比，有效地降低了有限元模型计算次数，提高了计算效率，与极限平衡法相比，提高了计算精度。

(3)综合考虑了土石坝土体中基质吸力与渗透系数之间的非线性关系，较为真实地反应了土石坝应力状态，建立了土石坝可靠度功能函数，不仅适用于本文在水位骤降情况下的坝坡可靠度分析，同时适用于大部分水力边界条件下复杂坝坡可靠度分析。