水工隧洞不同围岩等级力学性能研究
王 顺,贾 飞
(1.河北工业大学土木与交通学院,天津300401;2.西安理工大学水利水电学院,陕西西安710048)
隧洞是水工建筑物中极其重要的结构形式之一,特别是在水利工程的输调水工程中。有些隧洞长度要达数十公里,埋深在几千米之内,要穿越很多种不同的地质单元,遇到松散地层、断层破碎带、浅埋强风化、溶洞等地质情况。隧洞工程的工序繁多、技术复杂、施工比较困难,往往成为整个水利工程的控制性工程[1- 3]。隧洞的围岩稳定及支护结构安全是保证隧洞安全、实现隧洞功能的关键因素[4- 6]。深埋地下隧洞工程具有工作年限长、工程规模大、工程重要性等级高等特点,一旦引发围岩的稳定性问题将会给工程带来灾难性的破坏。因此,深入分析隧洞衬砌结构的稳定性,准确模拟隧洞围岩与支护结构的变形、应力特点,并对围岩条件差的危险洞段进行钢拱架结构整体加固,是许多学者和工程技术人员研究的热点[7- 10]。
针对隧洞的研究已取得了一定的成果,但大多局限于单一类型围岩,然而在实际的工程环境中,有些地区地质条件复杂,围岩等级明显下降。因此,探究围岩等级下降时对水工隧洞内力及变形产生的影响,有助于确保围岩稳定及施工安全,为同类工程提供参考。
1 研究方法
1.1 工程概况
某土建工程主要有拦河坝、连接洞、取水口、低压引水洞、调压井、压力竖井、压力钢管、地面厂房、尾水洞和进场公路。工程的基本特征要素如下:总水头233 m,净水头194.40 m,设计流量26.0 m3/s,装机容量48 MW(4×12 MW),设计洪水位1 836 m,最高运行水位1 835.9 m,最低运行水位1 832.0 m。
该工程从取水口到沉沙池的连接渠道长约80 m。渠道采用低压引水隧洞,洞长3 850 m,布置在左岸,钻爆法施工,进口底高程(沉沙室后)1 818.7 m,出口底高程(接调压井)1 804.0 m,最大埋深500 m,最小埋深40 m。进口和过沟拐点位置各布置1个施工支洞。引水隧洞断面呈城门洞形,顶拱半径1.5 m,底宽3.6 m,侧墙高2.3 m。
根据GB 50086—2001《锚杆喷射混凝土支护技术规范》中不同围岩级别划分可知[11- 12],该工程涉及到Ⅲ类围岩和IV类围岩。其中,Ⅲ类围岩主要为层间结合良好的薄层和软硬岩互层结构,以构造节理为主,节理面多数闭合,层间结合良好,约占总体围岩1/3;IV类围岩主要为层间结合不良的薄层和中厚层以及软硬岩互层结构,部分张开层间有泥质填充,多数夹泥层间错动明显,结构结合能力相对较差,约占总体围岩的2/3。
1.2 计算原理
Abaqus软件拥有能够真实反映围岩性状的本构模型,能够平衡初始地应力,可以精确模拟接触面的性状等优点,并提供了解决复杂接触关系的接触面模拟功能,对岩土工程有很强的适应性[13]。由于计算要考虑到锚杆、地层变形和地层塑形应变,本次采用地层结构法进行分析计算。
初始自重应力场通常可以用有限元方法得到,但必须满足平衡条件和屈服准则,工作量大,可能不收敛。鉴于丁文其[14]等提出新的方法在沉管中平衡地应力是可行的,此次应用于断面更大的隧洞中,探究其方法的可行性。首先将重力荷载施加于围岩,并根据实际工程施加边界条件,通过计算得到重力荷载作用下的应力场,再将应力场导出重新定义为初始应力场,和重力荷载一并施加到原有限元模型中,即可得到初始应力场。在保证各节点初始位移为0的同时,既满足平衡条件,又不违背屈服准则。
本次模拟施工采用软化模量法。在支护和衬砌施工前,先将待开挖区单元的弹性模量降低(本方案中降低40%),再根据施工顺序,依次模拟应力释放效应,喷锚支护的施加,最后再添加衬砌。
1.3 研究内容
本次模拟研究以引水隧洞为分析对象,主要包括:①利用丁文其等提出的方法进行地应力平衡,探究其方法用于隧洞的可行性;②基于Abaqus计算Ⅲ类和IV类围岩等效位移、等效塑性应变、支护水平位移、支护竖直位移、支护轴力、支护弯矩和锚杆轴力,根据Abaqus计算云图,取计算结果的最大值,描述其变化规律,分析最大内力及应变出现的原因;③就Ⅲ类和IV类围岩计算结果进行对比分析,对内力及变形突出位置加以加固与防护,并提出相关建议,达到优化设计,安全稳定的目的。
1.4 计算假定
假定如下:①材料变形性质假定为各向同性;②围岩按摩尔-库伦理想弹塑性模型考虑,混凝土及锚杆按线弹性模型考虑;③初始应力场仅考虑自重作用;④不考虑地下水在开挖过程中的作用。
2 模型计算
2.1 计算工况及参数
本文对Ⅲ类和Ⅳ类围岩采取相同的计算工况,即支护厚度15 cm,锚杆长度4 m,衬砌厚度30 cm,主要考虑围岩垂直松动压力、侧向松动压力、衬砌自重等荷载作用,进行有限元应力变形计算。根据工程地质勘察及设计成果,选取围岩、喷射混凝土、混凝土底板、二次衬砌、锚杆的材料参数。计算参数见表1。
2.2 计算方法
本次模拟隧洞计算模型坐标规定为:X轴为断面水平方向,向右为正;Y轴为断面竖直方向,向上为正;模型的左、右两侧为水平位移约束,上、下边界为垂直位移约束。为了更契合实际工程,IV类和Ⅲ类围岩分别打5根、7根锚杆。模型采用四边形单元进行网格剖分,模型共7 878个节点、7 802个单元。围岩采用平面单元模拟,支护、衬砌和锚杆采用梁单元模拟,计算范围是8倍的洞径。地层结构法模型见图1。

图1 地层结构法模型
3 结果分析
3.1 围岩变形
等效位移是3个方向的位移矢量和,是总位移,而且是相对位移。Ⅲ类和IV类围岩等效位移分布见图2。从图2中可以看出,Ⅲ类和IV类围岩等效位移分布图都是左右对称分布,最大位移都出现在隧洞底板中部,最大值分别为3.79×10-4、6.02×10-4m。

图2 等效位移分布(单位:m)
等效塑性应变描述整个变形过程中塑性应变的累积结果。Ⅲ类和IV类围岩等效塑性应变分布见图3。从图3中可以看出,Ⅲ类和IV类围岩等效塑性应变分布图都是左右对称分布,区域数值大于0的地方,表示材料已经屈服。Ⅲ类和IV类围岩最大塑性变形都出现在隧洞两侧中部,最大值分别为3.03×10-4、2.25×10-4,数值较小,未超过材料的破坏应变。

图3 等效塑性应变分布
3.2 支护内力及变形
Ⅲ类和IV类围岩支护水平位移见图4。从图4可知,Ⅲ类和IV类围岩支护水平位移分布图都不对称,但支护两侧水平位移大小都一样,只是方向相反而已。支护在外力的作用下由外侧向内侧产生变形,最大水平位移出现在支护两侧中部,最大值分别为2.27×10-4、2.86×10-4m。产生水平方向变形的主要原因是受到水平向围岩压力。

图4 支护水平位移(单位:m)
Ⅲ类和IV类围岩支护竖直位移见图5。从图5可知,Ⅲ类和IV类围岩支护竖直位移分布图都是左右对称分布。最大竖直位移都出现在支护顶部,最大值分别为2.44×10-4、3.24×10-4m,方向向下。竖直向变形的主要原因是受到竖直向围岩压力和重力的共同作用。
由于水平方向荷载仅为围岩压力,水平方向变形相对于竖直方向较小。但总体来说,支护在水平方向和竖直方向变形量都很小,其主要原因是支护在围岩与衬砌之间存在相互作用力,相互之间产生约束,从而使其变形受到了限制。
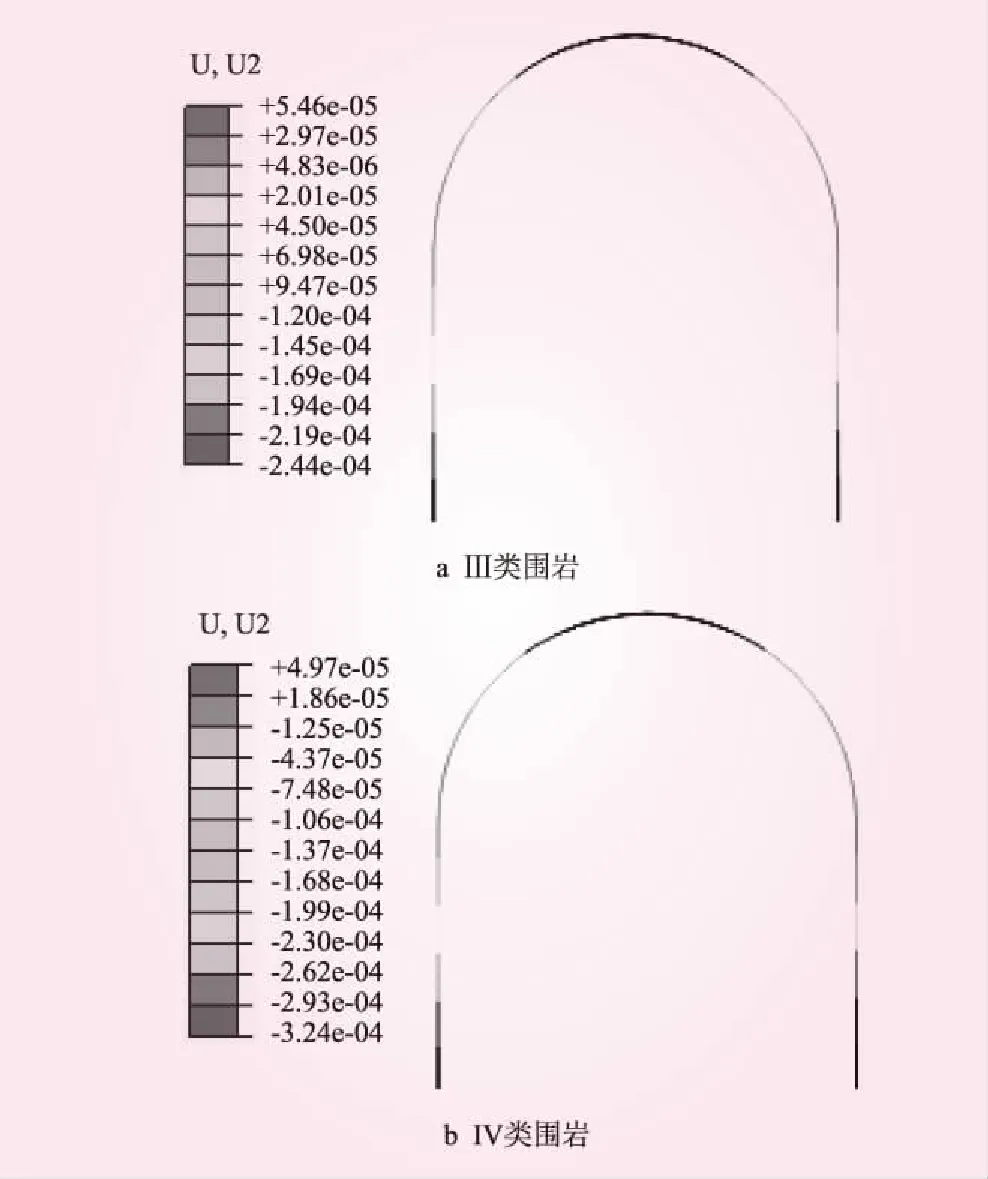
图5 支护竖直位移(单位:m)
Ⅲ类和IV类围岩支护轴力见图6。从图6可知,Ⅲ类和IV类围岩支护轴力分布图都是左右对称分布,最大轴力出现在支护底部和中上部,分别为1.32×105、1.71×105N。在外部围岩压力和重力的共同作用下,整个支护结构都处于受压状态。
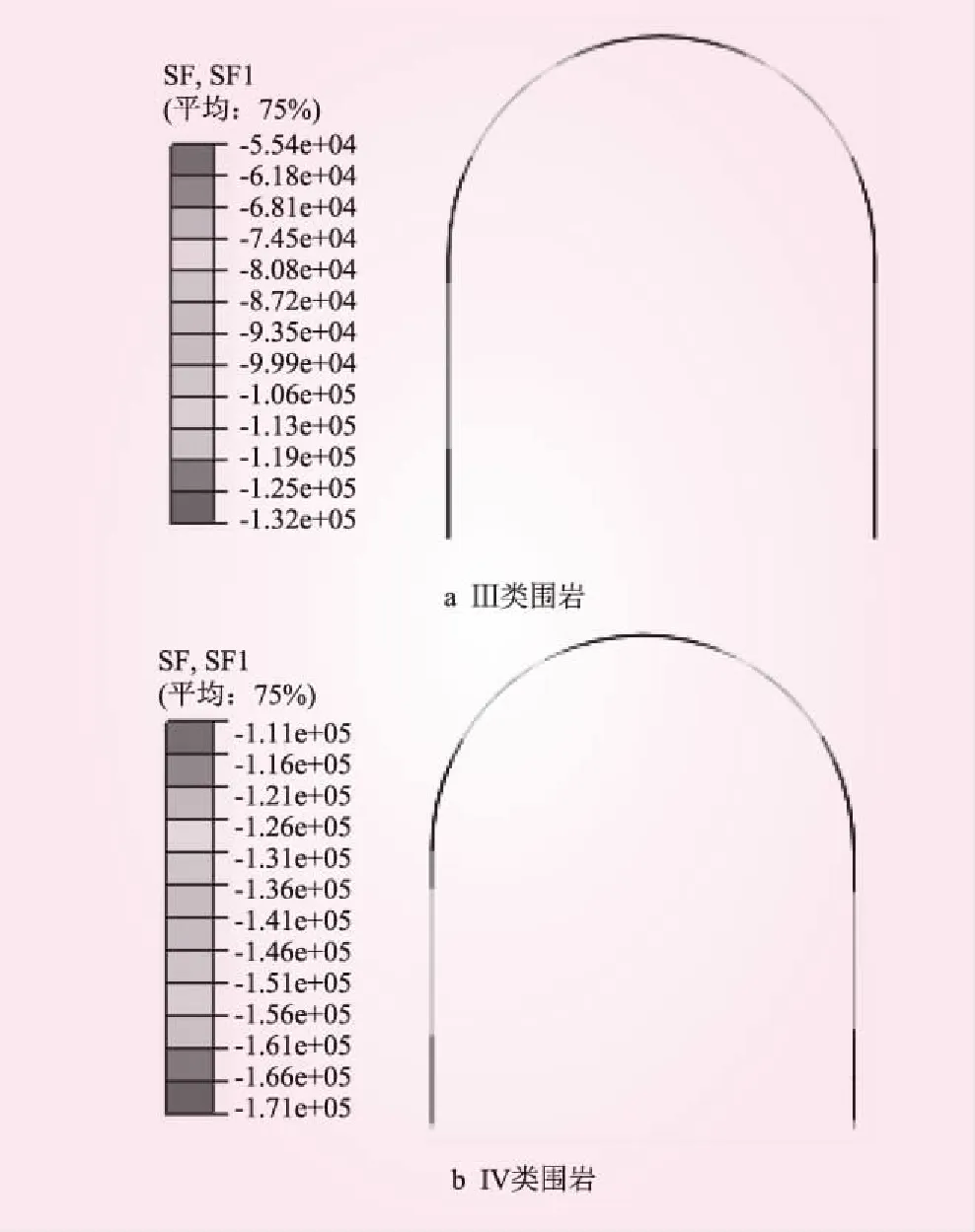
图6 支护轴力(单位:N)
Ⅲ类和IV类围岩支护弯矩见图7。从图7可知,Ⅲ类和IV类围岩支护弯矩分布图都是左右对称分布,最大弯矩出现在支护底部,最大值分别为3.63×103、8.71×103N·m,所受弯矩方向既有向内也有向外。
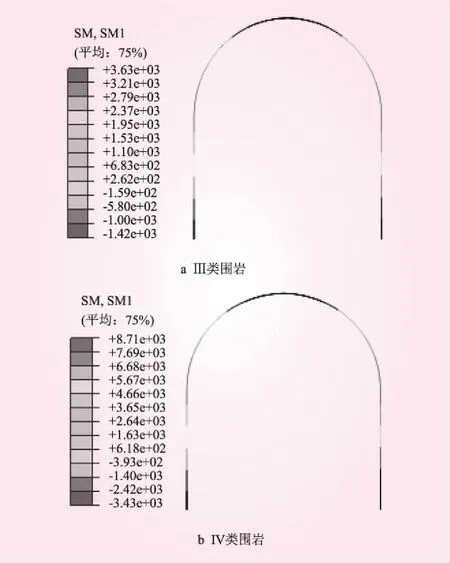
图7 支护弯矩(单位:N·m)
3.3 锚杆内力
Ⅲ类和IV类围岩锚杆轴力见图8。从图8可知,Ⅲ类和IV类围岩整体锚杆轴力分布图都是左右对称分布,最大值都出现在锚杆底端,图8a最下边2根和图8b最下边4根锚杆底端轴力分别达到最大,最大值分别为3.52×104、4.2×104N。由于锚杆对支护拉力作用,整个锚杆处于受拉状态,由外向内轴力逐渐增大。

图8 锚杆轴力分布(单位:N)
3.4 计算结果
Ⅲ类和IV类围岩计算结果见表2。从表2可知:

表2 不同级别围岩计算结果
(1)对于围岩变形,随着围岩级别下降,最大等效位移增加了58.84%,但围岩最大等效塑性应变减少了25.74%;对于支护变形,随着围岩级别下降,最大水平位移和最大竖直位移分别增加了25.99%、32.79%;对于支护内力,随着围岩级别下降,最大轴力和最大弯矩分别增加了29.55%、139.94%;对于锚杆内力,随着围岩级别下降,锚杆最大轴力增加了19.32%,增加率最小。
(2)虽然围岩等级不同,但二维有限元计算得到的内力及变形分布规律相似,且大部分分布图左右对称。各内力区及变形区变化较小,最大值出现的位置几乎没有发生改变,可能与工程地质条件变化较小,围岩级别相邻,Ⅳ类围岩比Ⅲ类围岩多打了2根锚杆,使得Ⅳ类围岩相应力学性能增加,变化趋势不明显等因素有关。可继续增加围岩种类,在围岩打入锚杆数量一样的情况下,得到更为系统的规律。由于洞室开挖造成岩体的临空面易失稳,应力波动比较剧烈,导致软弱、强度低的岩石破碎,破坏围岩的整体性和连续性,使围岩不能承受高的应力,不利于能量积累,容易出现应力降低带。因此,隧洞工程要求围岩等级不能太差。
4 结 语
本文基于地层结构法的三维有限元模型,利用了丁文其等提出的方法进行了地应力平衡,使得位移场基本为0,验证了此种地应力平衡方法在断面更大的隧洞中是可行的。与Ⅲ类围岩相比,Ⅳ类围岩除了围岩最大等效塑性应变减少外,其他大部分内力及变形都会增加,尤其支护最大弯矩明显增加,这个结果是Ⅳ类围岩比Ⅲ围岩多2根锚杆的前提下得出的,可见当锚杆数量取一样时,增加得会更多。支护弯矩最大值出现的地方容易产生应力集中,可能会影响隧洞施工安全,所以在此区段应增加锚杆,以此来降低支护所承受的内力。

