基于多星GPS-IR的雪深反演分析
任 超,郑中天,梁月吉,刘海锋,刘中流,杨 庆
(1.桂林理工大学测绘地理信息学院,广西桂林541004;2.广西空间信息与测绘重点实验室,广西桂林541004)
0 引 言
近年来,淡水资源日益紧张,全世界有1/6的人口是依靠积雪融化的水维持生活和生产,上游积雪的变化会影响下游的洪灾预警和水力发电等[1],监测积雪的变化具有重大意义。传统的积雪监测主要是靠地基的人工测量或其他自动测量方式,如超声波或伽马射线传感器,这些方法的时空分辨率很低[2]。使用卫星的遥感图像只能分辨是否有积雪,而不能判断出积雪的深度[3]。基于全球定位系统(GPS)信噪比的GPS干涉反射(GPS-IR)技术也可以监测测站周围的地表环境,具有监测范围广、连续性好的优点[4]。因此,GPS-IR可以作为传统积雪测量的重要补充手段。
国内外对GPS-IR雪深反演的研究已取得一定成果。Kristine M.Larson等根据GPS观测文件反演出的雪深数据研究发现,雪深反演结果和该地区发生的暴风雪时间之间具有很强的相关性[5];KarenBoniface等人利用GPS测站的观测数据,对美国西部地区的雪深进行了监测,反演雪深的均方根误差达到15 cm,相关系数大于0.6[6];Kegen Yu等结合多种载波信号对雪深进行反演,其结果优于现有的模型[7];Masaru Ozeki等根据多路径信号的振幅,研究了积雪表面的物理特性[8];戴凯阳等反演出了151d的雪深数据,并与实测雪深做了对比[9]。以上研究存在使用的卫星个数较少,没有综合多星反演结果等问题。基于此,本文提出了一种多星GPS-IR雪深反演分析方法,以期提高雪深反演的精度。
1 多星GPS-IR雪深反演原理
1.1 单星GPS
在GPS测量中,GPS接收机不仅接收直接来自卫星的直射信号,还接收卫星信号经地面、建筑物、水面等反射的反射信号,直射信号和反射信号产生干涉,引起多路径效应,形成合成信号,从而造成测量误差[10- 11]。信噪比主要受天线增益参数、接收机相关器的状态和多路径效应等方面的影响[12]。GPS观测文件中的信噪比数据能反映出多路径效应,从中可以提取出有关垂直反射高度的信息。图1为GPS-IR雪深反演示意。图中,H为天线高,是接收机天线的相位中心与地表的高差;h为接收机天线的相位中心与雪层表面的高差(垂直反射距离);hsnow为雪层厚度,是H与h的差值;α为卫星的高度角,由于反射点到天线相位中心的水平距离与到卫星的直线距离相比很小,故反射信号和直射信号的卫星高度角之间的差异可忽略不计。
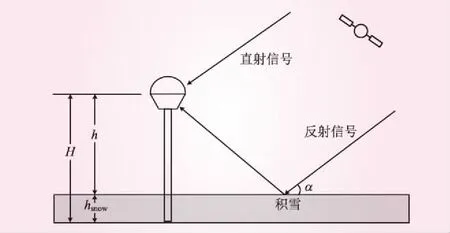
图1 GPS-IR雪深反演示意
接收机天线接收的合成信号的信噪比(Signal to Noise Ratio,SNR)与直射信号、反射信号的关系如下[1]
(1)
式中,Pd为直射信号功率;Pr为反射信号功率;φ为干涉相位。Pd和Pr项可以通过二次项拟合得到,两者是SNR的趋势项。
将SNR消除趋势项后,剩余残差可表示为
(2)
式中,dSNR为去掉趋势项后的信噪比;A为振幅;λ为载波波长。
在去掉SNR趋势项之前,应当将信噪比的单位由dB转换为volts,使之从指数变化转为线性变化,转换公式如下
(3)

dSNR=Acos(2πfx+φ)
(4)

在单星反演雪深中,因为反射信号极易受外部因素影响,如卫星状态、地形、反射介质等因素的影响,抗差性较差,容易出现跳变值,且单颗卫星用作反演雪深的观测时间段少,反演结果不能代表1 d的雪深值。
1.2 多星反演雪深方法
假设反演时长共m天,卫星数为n个,其反演结果表示为
(5)

本文将每天所有卫星的反演结果的平均值作为参考真值,并计算出当天反演结果的均方根误差(RMSE),第j天的RMSE计算方法如下
(6)
式中,n为卫星个数。
根据实际情况设置阈值为RMSE的倍数,本文根据试验结果设置阈值为1倍的RMSE。当有卫星的反演结果与参考真值的绝对差值大于阈值时,则判定该值为跳变值并剔除。完成跳变值的剔除后,对多颗卫星的反演结果求等权平均值,可以表示为
M=(R1+R2+,…,+Ri)/n
(7)
式中,M为多星反演结果。
多星反演雪深能够通过比较分析单星反演结果,剔除跳变,增强反演结果的可靠性,且多星反演采用多个时段,能够更好地反映当天的雪深。
2 实际应用
2.1 数据来源
本文采用的GPS观测数据来自美国板块边界观测(The Plate Boundary Observatory,PBO)项目中的P101测站,观测时段为2016年335年积日到2017年103年积日,共135 d,采样率为15 s。P101站位于美国的犹他州Randolph地区,北纬41.692°,西经111.236°,海拔高度为2 016.1 m,周围植被类型为灌木,测站高2m,每年被积雪覆盖的时间达100 d左右。该站采用的接收机类型为TRIMBLE NETRS,天线类型为TRM29659.00,整流罩类型为SCIT。P101站周围环境见图2。

图2 P101站周围环境
以2016年335年积日的PRN05号卫星为例,SNR观测值和拟合值见图3。从图3可知,在完整的观测时段内,卫星在上升段和下降段都是处于低高度角的状态,在此期间天线增益较小,多路径效应明显,SNR观测值较小,呈周期性波动,且波动明显,适合用作雪深反演。本文选取高度角在5°~25°内的数据反演雪深。

图3 SNR观测值和拟合值
以上升段为例,将图3中上升段5°~25°部分分离出来,转化单位后去掉趋势项,并将信噪比与历元变化改为与高度角正弦值的变化,然后进行Lomb-Scargle频谱分析,可以得到隐含有垂直反射高度的信息,频谱振幅峰值所对应的就是垂直反射高度。SNR残差单位转换和频谱分析见图4。

图4 SNR残差单位转换和频谱分析
2.2 数据处理
本文采用单星反演和多星反演2种方案。综合卫星的观测状况和观测质量,选取PRN02、PRN05、PRN09、PRN25和PRN27卫星进行试验,以PBO H2O课题组提供的雪深值作为实测雪深,用来对比分析。
单星反演结果和相关性分析见图5。从图5可知,在没有发生跳变的时间段,GPS单星反演结果总体与实测雪深吻合较好,相关系数都在0.90以上,平均相关性为0.951 6,能够一定程度上反映出雪深的变化趋势,但各卫星的反演结果在同一天几乎不相同,很难取舍。在某些天,GPS单星反演结果发生了跳变,影响了整体反演效果,PRN02卫星在2017年030年积日的跳变值最大,与实测雪深之间的绝对误差达到1.18 m。

图5 单星反演结果和相关性分析
使用本文方法,将5颗卫星的反演结果综合起来后,多星反演结果与相关性分析见图6。从图6可知,多颗卫星反演的结果与实测雪深吻合很好,能够很好地反映出雪深的变化趋势,相关系数达到0.993 3。与单星反演结果相比,多星反演结果消除了跳变,提高了反演结果的可靠性。此外,多星的相关系数与单星相比有了一定提高,其相关系数大于0.99,相比较于单星更适合应用于雪深监测。

图6 多星反演结果和相关性分析
为了进一步比较单星反演结果和多星反演结果,采用了RMSE和平均绝对误差(MAE)精度指标进行分析。不同卫星反演结果的精度指标见图7。从图7可知,RMSE精度指标分析结果为0.111 m,MAE为0.096 m,均优于单星的反演结果。可见,多星反演结果优于单星反演结果,证明了多星反演雪深的优越性。

图7 反演结果精度指标
3 结 语
本文针对单颗卫星反演结果各不相同、且容易出现跳变的缺点,采用了剔除跳变、等权平均的多星反演方法进行雪深反演分析。结果表明,多星反演结果与实测雪深的相关性达到0.993 3,RMES与MAE精度指标分析结果均小于各单一卫星。因此,基于多星的GPS-IR应用于雪深反演是有效、可靠的。为了进一步优化本文方法,后续将会对不同环境下多测站数据,以及如何消除单星跳变值、优化多颗卫星反演结果展开更为深入的研究。

