基于水文干旱指标的阿克苏河流域干旱特征分析

(1.新疆喀什地区水利水电勘测设计院，新疆 喀什 844000；(2.新疆塔里木河流域阿克苏管理局，新疆 阿克苏 843000)

我国是农业大国，气象干旱长期困扰着农业生产。据报道，我国平均每年受旱面积约2159.3万hm2，其中气象干旱约占60%，直接粮食损失约100亿kg[1]。目前，在干旱研究方面，以标准化径流指数(Standardized Runoff Index，SRI)为代表的水文干旱指标广泛地应用于世界各地[2-3]。阿克苏河流域位于新疆南部，该地区降水稀少，蒸发强烈，生态环境极度脆弱，“绿洲经济，灌溉农业”是其显著特点，干旱是农业的最大威胁。在已有文献报道中，鲜有基于水文干旱指数法研究的该流域干旱演化特征分析。鉴于此，本文以阿克苏河流域为研究区，根据其主要支流水文站多年径流数据，基于SRI指数，研究了流域干旱演化特征，以期为该地区农业抗旱减灾提供参考。

1 计算方法

1.1 水文干旱指标(SRI)

水文干旱是指因降水短缺而造成某段时间内地表水或地下水收支不平衡，使河流径流量、地表水、水库蓄水和湖水减少的现象。SRI(Standardized Runoff Index)作为水文干旱评价指标，其基本原理为：

首先，通过Box-Cox转换将径流序列转化为正态分布：

(1)

将式(1)结果进行标准化处理：

(2)

式中X——径流量；

λ——Box-Cox转换系数；

Y——经Box—Cox转换后序列；

σY——标准差。

SRI干旱等级划分标准见表1。

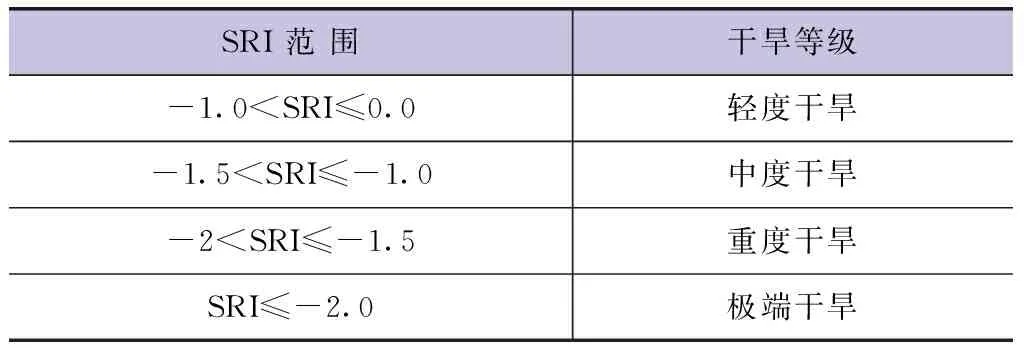
表1 SRI干旱等级划分标准

1.2 水文干旱识别方法

根据游程理论[4]，设定干旱阈值R0、R1、R2，当指标值小于、等于R0时发生干旱，当两次干旱事件(干旱历时和干旱烈度分别为d1，d2和s1，s2)之间只有1个时段的干旱指标大于R0但小于R2，认为这两次干旱是从属干旱，可合并为一次干旱事件，合并后的干旱历时D=d1+d2+1，干旱烈度S=s1+s2。对于历时只有1个时段的干旱事件，其指标值小于R1才被确定为1次干旱事件，反之计为是小干旱事件，忽略不计。游程理论示意如图1所示，其中干旱历时为D，干旱烈度为S，干旱间隔事件为L。

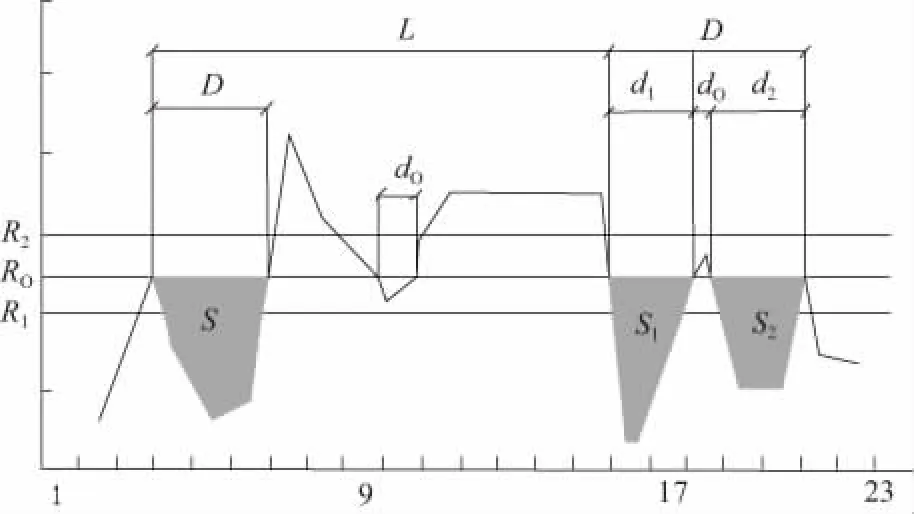
图1 游程理论示意

当连续出现干旱时，则出现连枯月，连枯月的游程概率计算式如下：

P=ρk-1(1-ρ)

(3)

ρ=(S-S1)/S

(4)

式中P——连续K月枯水发生概率；

ρ——模型分布参数，是指在前一月为枯水月条件下连续出现枯水的概率，可由长序列观测资料计算；

S——序列中枯水累积月数；

S1——包括K=1在内的各种长度连枯月发生频次的累计值。

1.3 水文干旱重现期及烈度

通过干旱历时和干旱烈度来描述干旱事件分析干旱频率时，需要计算两者联合概率分布函数，Copula函数是实现这种相关性分析的有效方法，其中最常用的函数有Gumbel-Hougaard、Clayton Copula和Frank Copula。令u=FD(d),v=FS(s)，则三者表示为[5]：

FD,S(d,s)=exp{-[(-lnu)θ+(-lnv)θ]1/θ}

(5)

FD,S(d,s)=(u-θ+v-θ-1)-1/θ

(6)

(7)

本研究采用相关指标法和极大似然法进行Copula函数参数估计[6]。

a.相关指标法

表2 Copula函数相关指标法参数估计

注表中τ为Kendall相关系数。

b.极大似然法

(8)

(9)

(10)

(11)

式中L(θ)——似然函数；u1=FD(d)；u2=FS(s)；

c[(u1,u2);θ]——二维Copula函数密度函数。

二维Copula函数经验频率计算式如下：

Po(i)=(mi-0.44)/(n+0.12)

(12)

式中mi——联合观测样本中满足条件D≤di且S≤si的观测个数；

n——样本容量。

采用均方根误差评定各种Copula函数拟合结果，计算式为：

针对上述方法存在的问题，本文以文献[1]的测量方法为参考，设计了测量链路，研究了互调发射测量数据随被测发射机与干扰信号源间链路衰减量变化的规律，提出了通过调节测量链路衰减量以实现互调发射抑制比的精确测量方法.实测验证结果表明，这种方法可操作性较好，能够准确测量多种类型的互调发射抑制比，易于实现自动化测量.

(13)

式中Pc(i)——理论联合频率值；

Po(i)——经验联合频率值。

根据重现期来描述干旱事件的严重性，干旱历时与干旱烈度联合分布的重现期包括D>d或S>s和D>d且S>s以下两种情况：

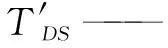
2 结果分析

2.1 流域干旱历时与干旱烈度分析

根据协和拉站(阿克苏河支流库玛拉克河控制站)、沙里桂兰克站(阿克苏河支流托什干河控制站)及阿拉尔站(塔里木河干流控制站)1961—2016年的SRI-1序列，选取阈值水平R0=0、R1=-1、R2=1对干旱事件进行提取：ⓐ协和拉站1961—2016年间发生过41场干旱事件，平均干旱历时为8.02个月，干旱烈度为4.99，最长干旱历时39个月，发生在1974年6月—1977年8月，对应的干旱烈度为历史最大值；ⓑ沙里桂兰克站发生36场干旱事件，最长历时干旱发生在1961年1月—1964年5月，干旱烈度达37.35，最大烈度干旱发生在1984年9月—1987年6月，干旱历时长达34个月；ⓒ阿拉尔站发生60场干旱事件，最长历时干旱发生在1990年11月—1991年12月，干旱烈度为7.14，最大烈度干旱发生在1974年9月—1975年9月，干旱历时达13个月。统计结果见表3。

表3 各水文站干旱特征统计结果

通过各水文站连续枯水的游程概率，可以看出协和拉站和沙里桂兰克站出现连续枯水1—2个月的概率较高，阿拉尔站出现连续枯水1—4个月的概率较高，如图2所示。

图2 各水文站点连枯游程概率

综合分析各水文站点的干旱特征：ⓐ协和拉站20世纪80年代以前的干旱事件具有长历时、高烈度的特点，在20世纪80年代之间干旱事件具有长历时、低烈度的变化趋势，进入20世纪90年代以后协和拉站进入偏湿期，干旱事件常有短历时、低烈度的特点；ⓑ沙里桂兰克站20世纪90年代之前干旱事件频发，而且各场次干旱持续时间较长，干旱烈度较大;20世纪90年代之后干旱烈度偏小，干旱事件发生较少；ⓒ阿拉尔站进入20世纪90年代之后，干旱灾害频发，且连续枯水的持续时间长，干旱烈度较大，干旱形势日趋严峻。

干旱历时与干旱烈度具有正相关性，即干旱历时越长，对应的干旱烈度越大。各站点干旱历时与干旱烈度Pearson相关系数均达到0.85以上，具有很好的相关性。以协和拉站为例，对干旱历时和干旱烈度进行频率分析，假定干旱历时与干旱烈度分别服从指数分布和Gamma分布，应用极大似然法估计参数，同时采用Kolmogorov-Smirnov进行检验，干旱历时和干旱烈度K-S统计检验值分别为0.1071和0.1268，显著水平0.01对应的临界值是0.2546，因此可认为干旱历时和干旱烈度分别服从指数分布和Gamma分布，如图3所示。

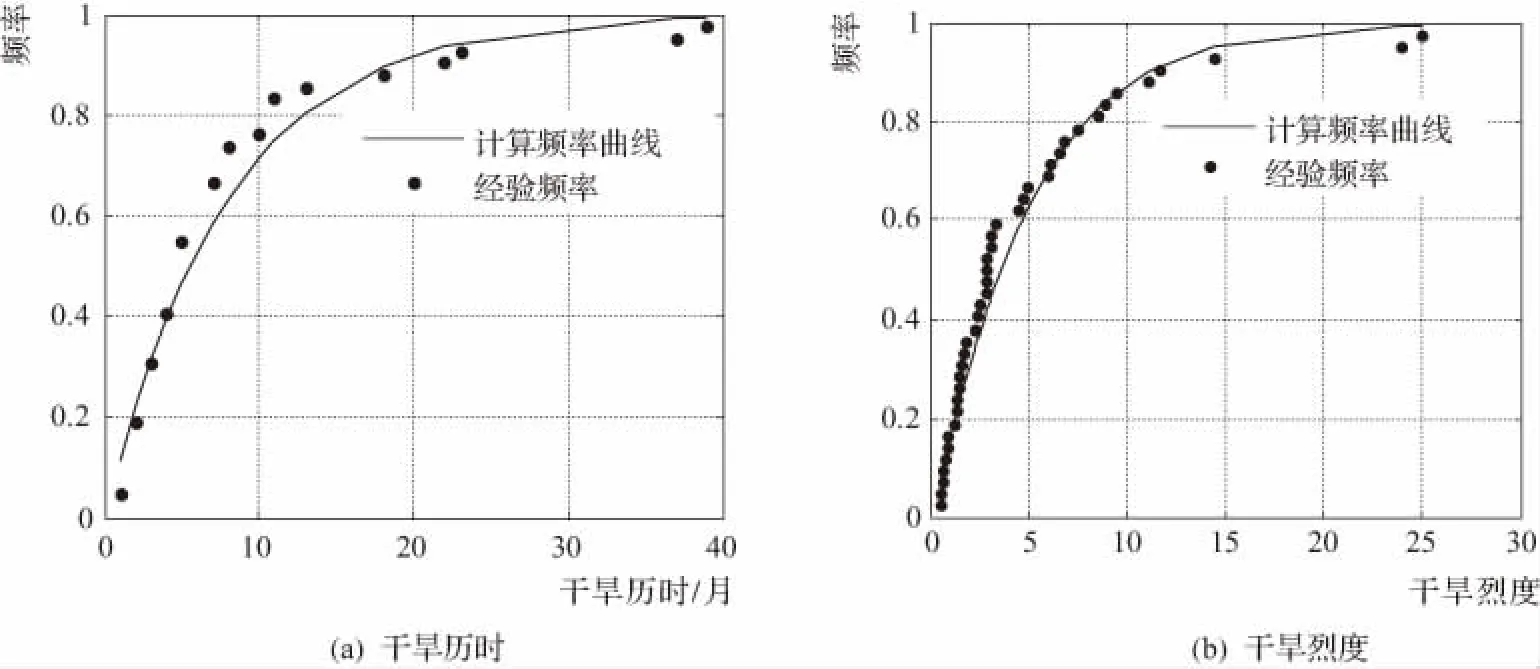
图3 协和拉站干旱特征

采用上述三种Copula函数建立干旱历时与干旱烈度的联合分布，分别运用相关指标法和极大似然法估计Copula函数参数，绘制了两种参数估计方法的理论与经验频率的相关图，如图4所示。

利用均方根误差检验不同Copula函数和不同参数估计方法对实测干旱历时和干旱烈度的拟合程度，

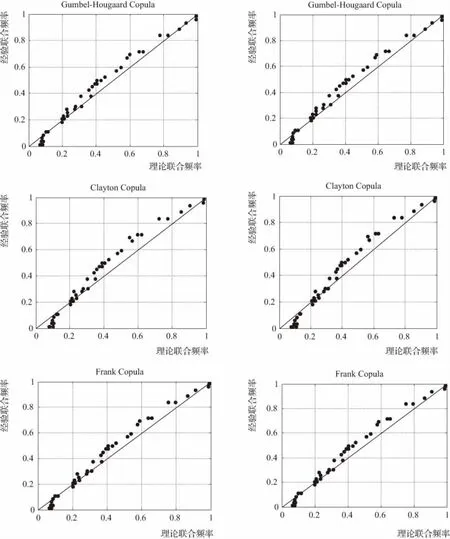
图4 不同方法对实测干旱历时及干旱烈度拟合比较

结果表明：协和拉站的干旱联合概率分布应选用Gumbel-Hougaard Copula函数，沙里桂兰克站选用Frank Copula函数，阿拉尔站选取Gumbel-Hougaard Copula函数；采用极大似然法较相关指标法拥有更好的估计效果，可得到干旱历时与干旱烈度的最优联合概率分布，结果见表4。

选取不同的边缘分布重现期得到联合分布重现期，当边缘分布的重现期为100年时，协和拉站实际发生干旱的重现期在76.7—143.5年之间(见表5)。

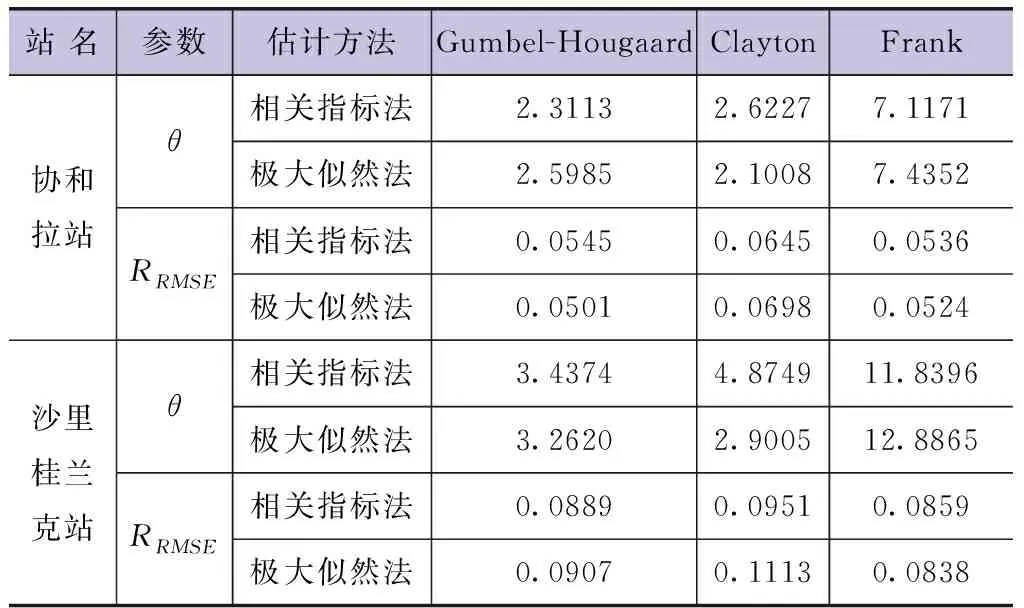
表4 水文各站Copula参数估计及评价指标计算结果

续表

根据协和拉站干旱要素同现重现期与联合重现期分布图，协和拉站1974年6月—1977年8月的干旱事件，干旱历时达到170年一遇的水平，对应的干旱烈度重现期为280年一遇，两者的联合重现期是155年，而同现重现期TDS则达到了330年一遇的水平，如图5所示。

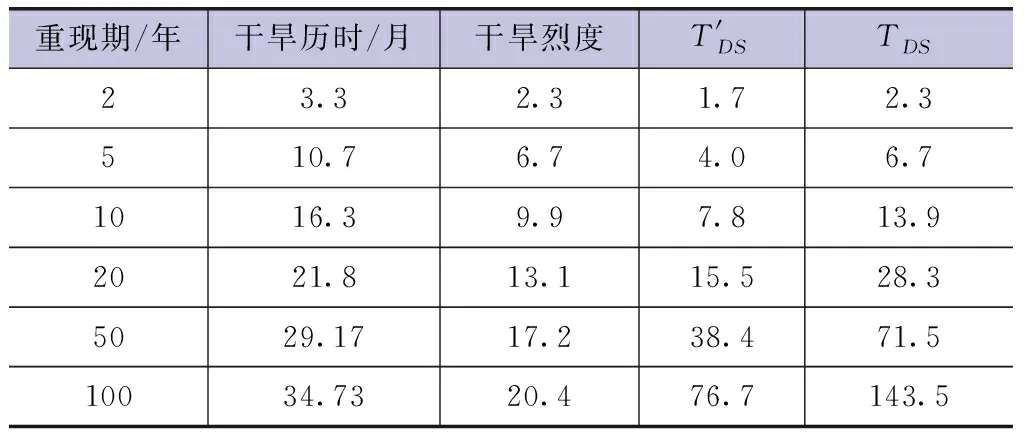
表5 协和拉站不同重现期下的干旱历时与干旱烈度

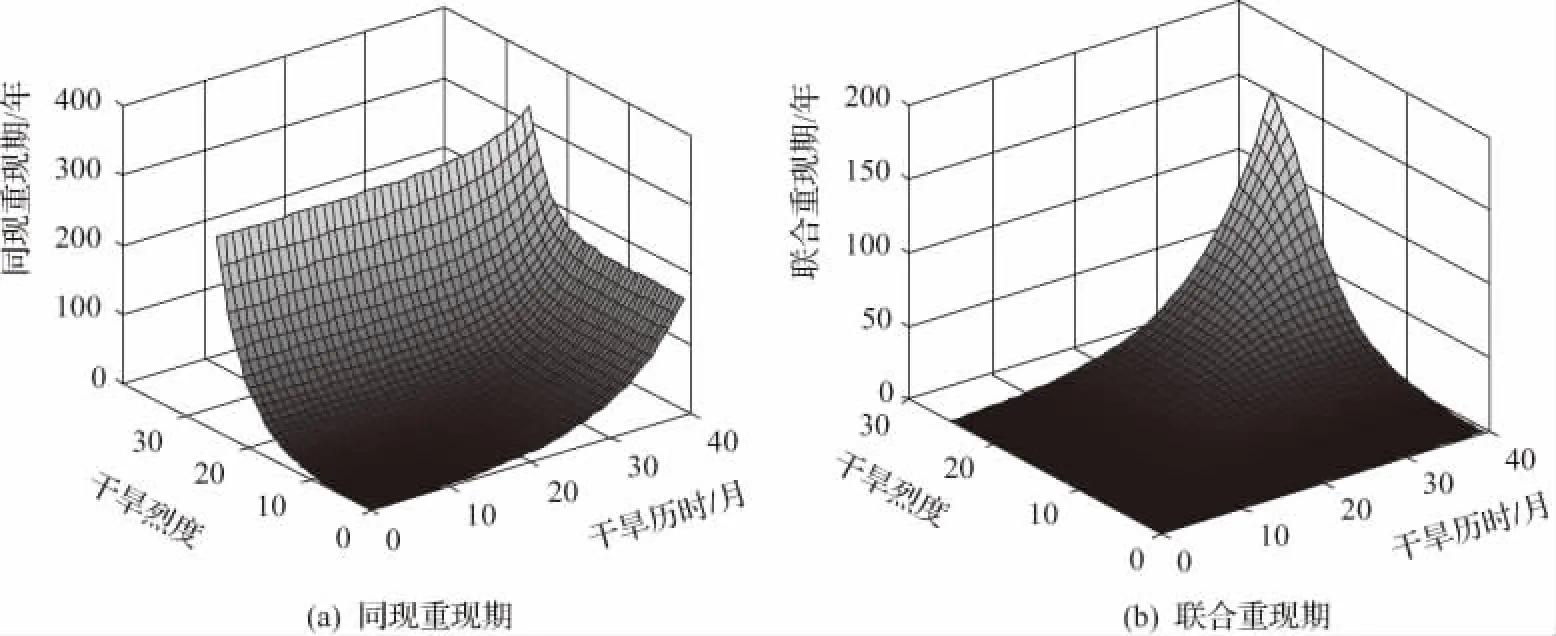
图5 协和拉站干旱要素同现重现期与联合重现期分布

2.2 流域水文干旱演变趋势分析

由于春季来水量关系到春季可引用水量，采用谐波周期法对流域主要代表水文站的SRI33-5月的指标值进行周期识别，发现沙里桂兰克站春季径流量具有同样的丰枯演变周期，演变周期为11.75年；阿拉尔站春季旱涝演变周期为4.7年与7.8年的混合演变周期；协和拉站无明显的周期变化；通过各站主震荡周期可以预测出未来一段时期内阿克苏河春季径流量将处在一个由偏丰逐渐向偏枯转变的阶段，各站点演变周期能够为未来流域旱情预测提供重要的参考价值。

3 结 语

本文根据阿克苏河流域1961—2016年逐月径流资料，采用水文干旱指标(SRI)，对研究区干旱演变特征进行了系统分析。结果表明：阿克苏河源流自2000年以来均处于丰水阶段，塔里木河干流均处于枯水阶段；进入20世纪90年代后，流域上下游干旱事件历时长短、烈度高低各有不同，干旱形势日趋严峻；未来阿克苏河春季径流将处于由偏丰向偏枯转变的阶段。研究结果为丰富流域干旱研究，合理配置水资源，缓解流域内供需水矛盾及抗旱减灾提供了科学参考。