河流健康评价指标权重分析

(安徽省·水利部淮河水利委员会水利科学研究院 水利水资源安徽省重点实验室，安徽 蚌埠 233000)

人类社会的发展与河流密不可分，河流不仅为人类提供日常生活所需的用水，同时也为人类经济社会发展提供必需的工农业用水，而且河流在人类的社会活动中还能提供航运交通、商业开发、休闲娱乐等诸多的服务功能[1]。河流的健康与否不但影响河流自身的发展演变，同时也会影响人类的生存和发展[2]。一旦河流受到污染遭到破坏，势必会对人类的经济社会发展产生影响。因此人类在开发利用河流的同时，需要遏制河流的健康恶化。

要遏制河流的健康状况恶化，需要了解河流的健康状况以及明确如何判定河流的健康状况，并分析河流健康评价指标的重要性，将其进行排序，可在后期河流健康治理方面有针对性地对河流进行保护或者修复。

1 评价指标体系构建

河流健康评价指标体系通常采用3级体系，即目标层、准则层、指标层[3]。目标层为河流健康状况，准则层则包括自然形态、生态环境、社会功能3方面，指标层则为针对河流健康提出的具体评价指标。其结构体系见下图。

a.目标层A。通过河流健康评价指标体系各评价指标的分析，对河流的健康状况进行综合评价，确定河流所处的健康状态，并发现威胁河流健康发展的问题，从而为指导河流的开发利用、管理以及保护提供科学依据[4]。

评价指标体系结构图

b.准则层B。包括3方面准则：自然形态方面、生态环境方面和社会功能方面。

c.指标层C。针对准则层3个方面，建立对应各准则层下的具体评价指标，并给出具体评价指标的计算方法或者评判标准，以及具体的健康刻度分值，就可对评价指标的健康分值进行定量或定性计算。

通过对各种标准、文献、规划、文件等资料中的有关评价指标的综合分析，对评价指标筛选结果，构建河流健康评价指标体系，并约定河流健康评价标准分为5个等级，分别为“理想状况”(80～100分)、“健康”(60～80分)、“亚健康”(40～60分)、“不健康”(20～40分)和“病态”(0～20分)，具体河流评价指标体系健康刻度见表1。

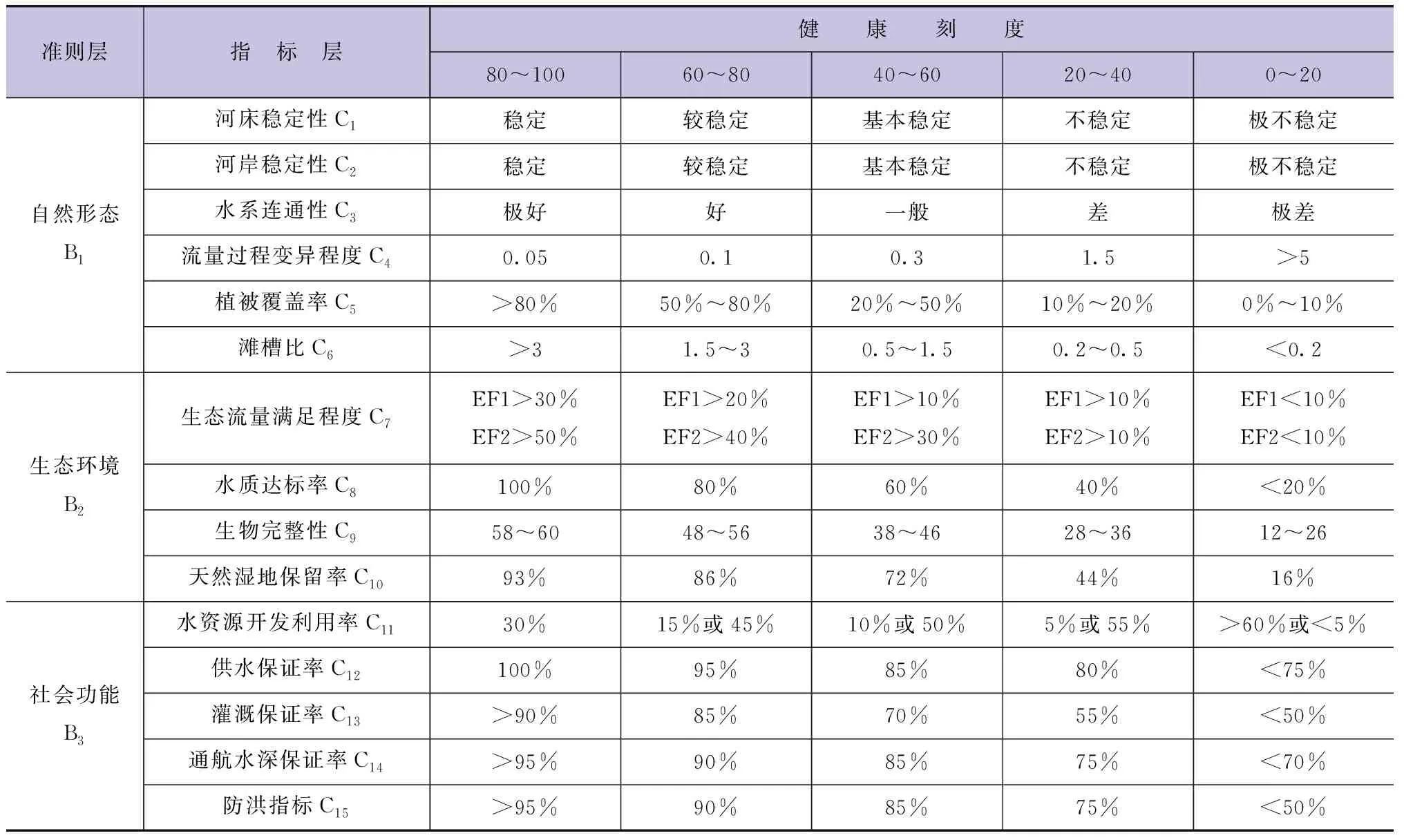
表1 河流评价指标体系健康刻度表

2 层次分析法简介

河流健康评价指标权重分析采用层次分析法(AHP)。层次分析法本质上是一种“分解—判断—综合”的基本决策思维过程[5],步骤如下。

2.1 建立递阶层次结构

根据属性的不同对评价指标进行分类组合，形成一种“目标层—准则层—指标层”递阶层次结构。

2.2 构造两两比较判断矩阵

运用“1～9”比较标度法把各因素之间的相对重要性判断结果用数值表示。准则层的自然形态、生态环境、社会功能3方面因素进行两两比较，对重要性进行赋值，据此构建准则层的判断矩阵。同理，构建各指标层的判断矩阵。

2.3 层次单排序

计算构建的准则层判断矩阵的最大特征根及对应的特征向量，可以计算得出3个准则层对应目标层所占权重，同理计算出各具体指标对应准则层所占的权重，然后进行层次单排序分析。层次单排序的两个关键问题是对构造的判断矩阵进行最大特征根和特征向量的计算，采用求和法。

将矩阵按列归一化：

(1)

式中aij——因素i与因素j重要性比较结果，为判断矩阵的组成因素。

按行求和：

vij=∑bij

(2)

归一化：

(3)

2.4 一致性检验

权重分配计算是否合理，还需要通过一致性检验确定。计算步骤如下：

(1) 计算一致性指标C.I.

(4)

式中n——判断矩阵的阶数；

λmax——判断矩阵的最大特征根，可由下式求出：

(5)

式中W——权重向量矩阵；

A——判断矩阵。

(2)随机一致性指标C.R.

(6)

其中，R.I.为平均随机一致性指标，对于低阶的平均随机一致性指标可以通过查表得出，其具体取值见表2。

表2 平均随机一致性指标

2阶以下的判断矩阵，R.I.为0，上述计算公式无意义，此时规定C.R.为0，即表示判断矩阵总是具有完全一致性。对于3阶及3阶以上的判断矩阵，当C.R.≤0.10时，认为判断矩阵的一致性令人满意；当C.R.>0.10时，则认为判断矩阵的一致性存在较大的偏差，需要重新调整之前构建的判断矩阵，直到最后的计算结果满足C.R.≤0.10时，表明此时建立的判断矩阵一致性检验合格，先前通过层次单排序分析得到的权重顺序是合理有效的。

2.5 层次总排序及其一致性检验

层次总排序是指在层次单排序的结果基础上，综合分析得出最底层(指标层)对于最顶层(目标层)的相对重要性权值。层次总排序同单排序一样也需进行一致性检验。C.I.、R.I.和C.R.的计算公式为：

(7)

(8)

(9)

层次总排序的一致性检验方法同层次单排序一样，若总排序的一致性检验合格，则所求得的指标权重就是指标的最终权重。

3 评价指标权重分析

通过层析分析法对准则层及各指标层的权重进行计算。

表3 准则层权重分配表

通过MATLAB数学软件计算得：A-B判断矩阵的λmax=3.0092，C.I.=0.0046，C.R.=0.0079<0.10，判断矩阵一致性检验合格，λmax所对应的特征向量进行归一化得到W=(0.1634,0.5396,0.2970)T，W的各个分量值就是各评价指标的权重,具体权重分配见表3。

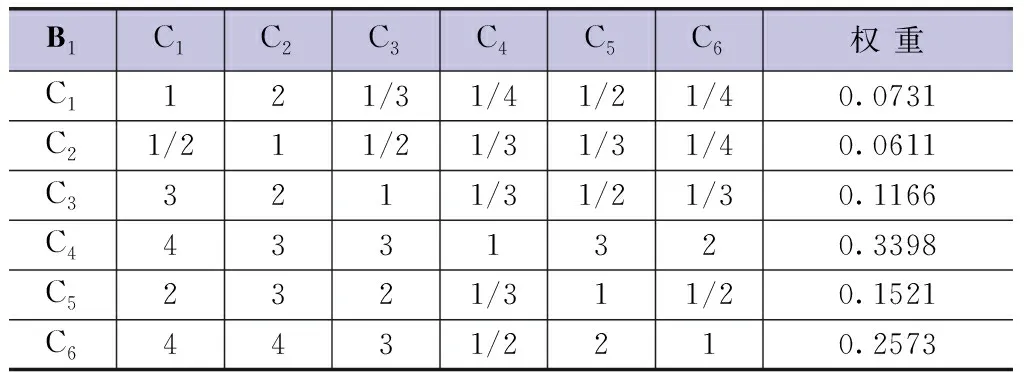
表4 自然形态准则层指标权重分配表

通过MATLAB数学软件计算得：B1-C判断矩阵的λmax=6.2879，C.I.=0.05758，C.R.=0.0464<0.10，判断矩阵一致性检验合格，λmax所对应的特征向量进行归一化得到W=(0.0731,0.0611,0.1166,0.3398,0.1521,0.2573)T，W的各个分量值就是各评价指标的权重,具体权重分配见表4。

表5 生态环境准则层指标权重分配表

通过MATLAB数学软件计算得：B2-C判断矩阵的λmax=4.0813，C.I.=0.0271，C.R.=0.0301<0.10，判断矩阵一致性检验合格，λmax所对应的特征向量进行归一化得到W=(0.2184,0.1452,0.5340,0.1023)T，W的各个分量值就是各评价指标的权重,具体权重分配见表5。

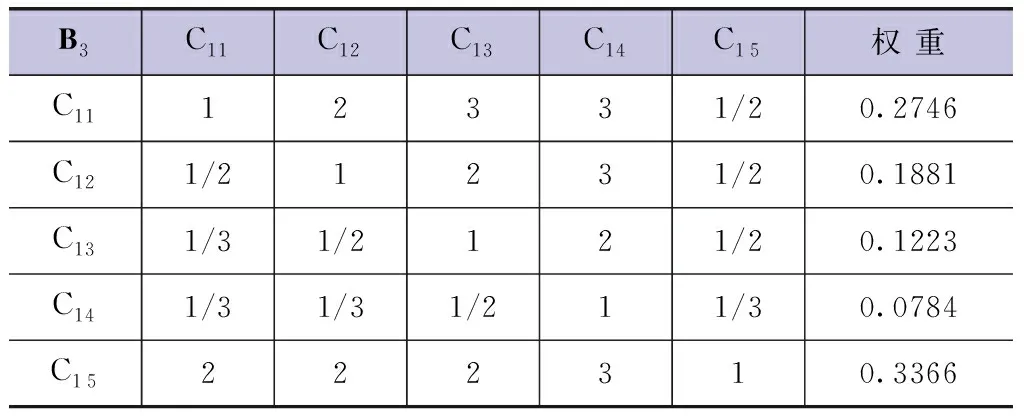
表6 社会服务准则层指标权重分配表

通过MATLAB数学软件计算得：B3-C判断矩阵的λmax=5.1759，C.I.=0.0440，C.R.=0.0393<0.10，判断矩阵一致性检验合格，λmax所对应的特征向量进行归一化得到W=(0.2746,0.1881,0.1223,0.0784,0.3366)T，W的各个分量值就是各评价指标的权重,具体权重分配见表6。

根据准则层及各指标层权重分配计算结果，确定河流健康评价指标体系中所有评价指标在河流健康评价指标体系中的权重,具体综合权重分配见表7。

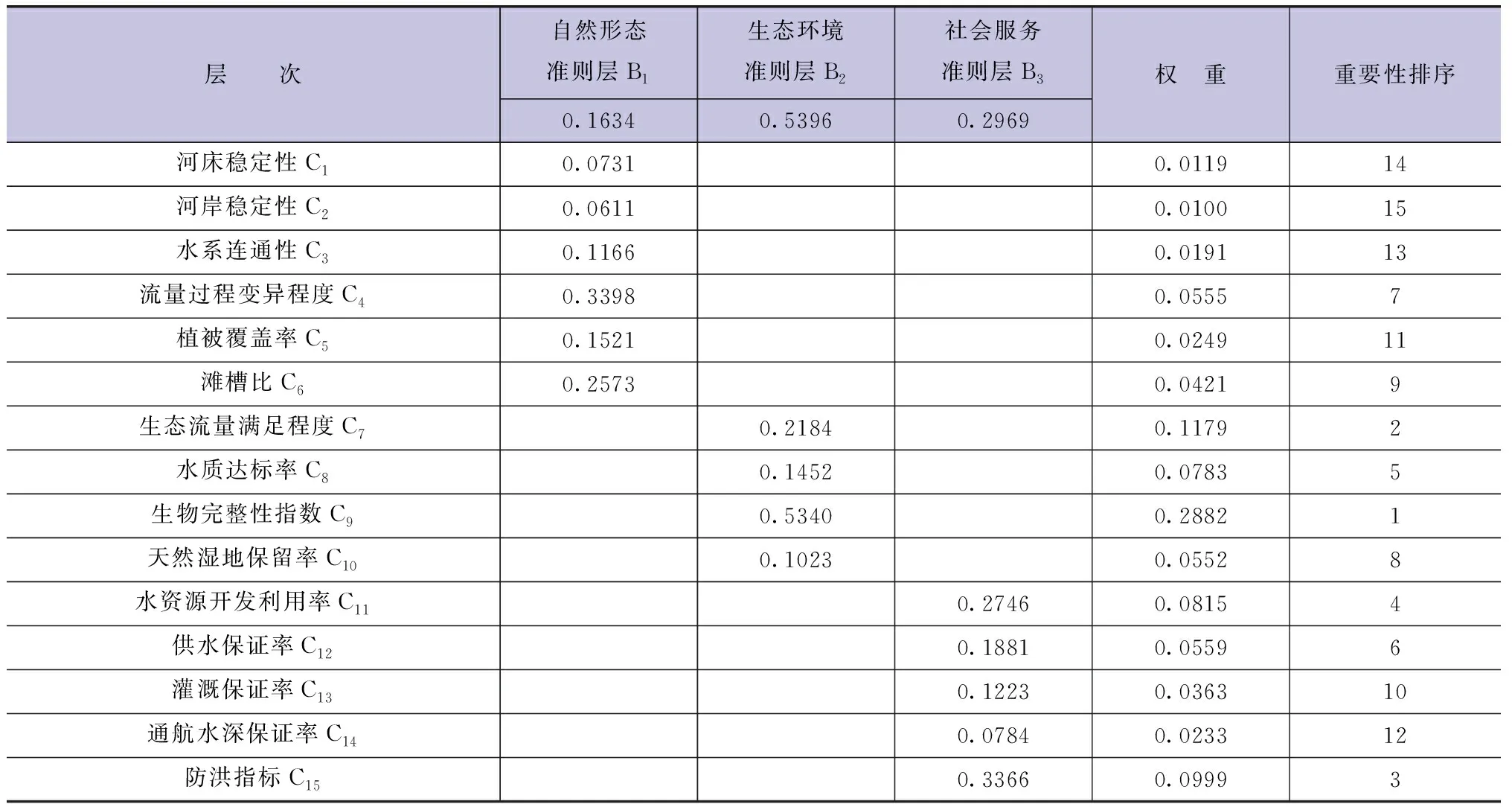
表7 河流健康评价指标体系综合权重分配表

运用公式(7～9)进行层次总排序的一致性检验，计算过程如下：

经计算得出层次总排序的一致性检验合格，所求得的指标权重就是评价指标的最终权重。

4 结 论

通过指标权重分析得出，河流的健康与否与生态环境有着重要联系，其中生物完整性指数及生态流量满足程度的权重占比达到总指标的40%，因此，在河流健康及修复保护方面，应当优先考虑对生态环境的治理保护。