一种基于重要点的时间序列分段算法
孙志伟,董亮亮,马永军
天津科技大学 计算机科学与信息工程学院,天津 300222
1 引言
时间序列是指按照时间先后顺序排列的各个观测记录的有序集合,广泛存在于商业、经济、科学工程和社会科学等领域。随着时间的推移,时间序列通常包含大量的数据。如何对这些时间序列数据进行统计和分析,从中发现一些有价值的信息和知识,一直是用户感兴趣的问题。近年来,时间序列数据上的数据挖掘研究受到普遍关注,包括关联规则挖掘、相似性查询、模式发现、异常检测等。由于时间序列数据的海量和复杂的特点,直接在时间序列上进行数据挖掘,不但在储存和计算上要花费高昂代价,而且可能会影响算法的准确性和可靠性。为了提高数据挖掘算法的准确度和有效性,需要首先对时间序列做预处理,以一种精简的近似表示来代替原始的时间序列数据。
人们对时间序列数据的近似研究做了大量的研究工作,国内外提出了很多时间序列模式表示的方法[1-2]:基于频域方法[3],基于奇异值分解、符号化[4]表示方法以及分段线性表示[5-6]方法。分段线性表示(Piecewise Linear Representation)方法是通过提取原时间序列上反映序列趋势走向的主要特征点,用连续的、首尾相连的直线段来近似表示原序列,具有简单直观,数据压缩率高等特点,是一种数据压缩和消除噪声的有效方法,因此对时间序列线性表示的研究具有重要意义。
按照分段方法的不同,基于分段的表示法可分为以下几种:
第一种称为PAA(分段近似聚合),通过对时间序列进行等间隔划分,用每一段的平均值来近似描述整个序列[7-8],即将给定时间序列转换为只包括K个直线段的近似序列,但是不能控制每一子段和全段的误差。PAA方法在不考虑实际序列形状的情况下,仅仅采用等分的方法,不能很好地保留原始序列的变化趋势。
第二种称为PLR(分段线性表示),将时间序列数据表示为相邻的线段簇,用若干条首尾相邻的直线段来近似代替原有时间序列,间隔并不一定相等。对于每个分段内部,一般采用线性插值或者线性回归的方法拟合数据。分段线性表示方法一种是采用拟合误差的方法进行分段,代表人是Keogh[3]。在Keogh的分段表示方法中,分段近似的目标是使原时间序列与其线性近似表示之间的残差平方和最小。这种方法又可以细分为两种:其一使用局部阈值来控制单个分段,让当前子段的误差不超过该局部阈值,其二是使用全局阈值,让所有分段的误差和不超过该阈值。文献[9]介绍了三种该类型的具有代表意义线性分段算法:即滑动窗口(SW)、自顶向下(TD)、自底向上(BU)。其中,SW支持时间序列的在线分段,但分段效果一般[10],而且不支持保留分段历史信息以及二次拟合[11]。相比之下,TD和BU算法尽管分段效果较好,但不支持对时间序列进行在线分段[12],而且算法空间复杂度较高。此外,文献[13]提出了一种基于时态边缘算子的时间序列分段算法,文献[14]提出一种基于斜率提取边缘点的时间序列分段算法,基于斜率提取边缘点的时间序列分段线性表示方法中提出了基于某点与左右两侧相邻点之间连线的斜率差来进行判断的方法,斜率差大于某个阀值时,即将其加入边缘点的集合。基于时间序列趋势转折点的分段线性表示法将极值点和变化幅度大于某一阀值的点列为转折点[15]。上述度量方法的共同缺陷是需要事先指定一些不容易确定的参数,如斜率的阀值、变化幅度的阀值,并且只考虑了局部的情况,对整体考虑不足。
另外分段线性表示还包括采用寻找重要点的方法,主要是存储对序列走势有重要影响的点[16-18]。而基于重要点的方法很符合人们的视觉印象,可以保留整个序列中重要的趋势情况,但需要准确对重要点进行定义。周大镯等证明了正交距离和垂直距离的等效性,并提出了基于序列重要点分割算法PLR_SIP[19]。该方法采用递归调用的方法,一直对最左侧序列进行分解,直到拟合误差小于用户指定的某个值,不能根据用户的需要找出最重要的指定个数的点,即用户参数不易设定,无法根据用户的需要选择压缩的程度。陈然[20]提出的基于重要点的时间序列固定分段数分段算法,采用每一段的拟合误差作为优先级的标准,同时设置了误差阈值作为输入参数,但是误差阈值的参数值不太好估计。
本文提出的方法通过分析原始曲线与拟合曲线,首先考虑到了拟合误差的大小和序列长度,接着针对优先级较高的分段进行预分段处理以期找到最优的分段,并在分段时考虑分段中多个重要点(最大值点和最小值点)的同异向关系,可以一次划分成多段,从而在压缩率一定的情况下,保证了反应时间序列曲线总体特征的同时,大大提高了固定点分段的效率;而且方法参数容易确定,除数据集外只需要输入压缩率或者分段数量,用户非常容易确定。
2 时间序列的概念和问题描述
2.1 相关概念
2.1.1 时间序列
时间序列数据中间的每个观察结果可形式化定义为元组(v,t)。v为待观察变量的值,可以是股票的价格、某地的温度、网络事件的评价等;t为观察时刻的时间戳,一个时间序列包含若干个这样的元组{(v1,t1),(v2,t2),…,(vn,tn)},其中t1,t2,…,tn,按照时间先后顺序有序排列。一般情况下,时间序列的采样间隔时间Δt=ti-ti-1相等,可以看出t1=0,Δt=1,此时将时间序列X={x1=(v1,t1),x2=(v2,t2),…,xn=(vn,tn)}简记为X={x1,x2,…,xn}。
2.1.2 时间序列的分段线性表示
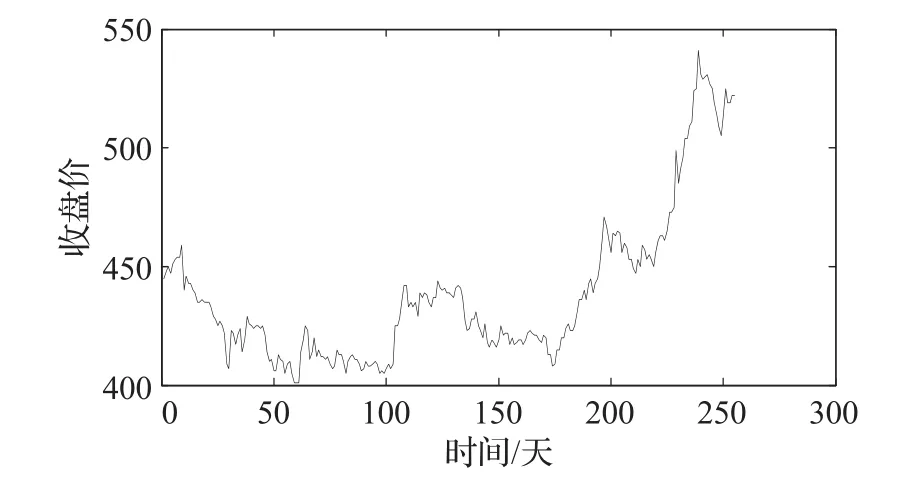
设有时间序列X= 其中,wi表示时间区间[wi-1,wi]的两个端点的坐标,fi(t,wi)表示连接模式wi两端点的线性函数,ek(t)是一段时间内时间序列与它的模式表示之间的误差。 2.1.3拟合误差 设时间序列,通过线性分段算法得到时间序列的PLR表示为: 其中L(⋅,⋅)表示连接两点的直线段。将L(X)经过线性插值后得到的时间序列记为,那么该PLR表示与原始时间序列之间的拟合误差定义为: 2.1.4 时间序列分段线性表示的压缩率 设时间序列X= 2.1.5 时间序列分段拟合差值的最大值和最小值 分段拟合差值定义为原始曲线与拟合曲线对应的点做差,表示为(参照垂直距离计算),拟合误差的最大值定义为一段时间序列中,拟合差值的最大值,表示为,分段拟合误差的最小值,定义为一段时间序列中,拟合差值的最小值,表示为 重要点探测技术最早由Chung[21]等提出,在时间序列分段算法中可用该方法生成一连串重要点序列作为时间序列的分段点,从而达到线性拟合的目的,重要点即是时间序列中dis最大的点,dis见公式(2),如图1所示,对于整段序列来说,点B是距离序列首尾连线垂直距离最大的点(文献[19]中,周大镯等已经证明使用垂直距离相对于使用正交距离的优越性),所以点B是序列重要点。垂直距离:从B向AC引垂直线段,与AC交于D,BD的长度,即: 图1 重要点分析 本文从不同角度提出了自己的三点看法: (1)在图2中,A段表示时间序列中X轴为0~3表示的分段,B段表示时间序列中X轴5~6表示的分段,按照拟合误差的公式(1)计算,A段的拟合误差比B段的拟合误差稍大,如果按照陈然[20]提出的分段优先级按照拟合误差的大小进行排序,应该先对A段进行分段,但是,显然B段的波动比A段更大,而且B段只需要一次分段即可更好地拟合,因此B段应该优先分段,所以只考虑拟合误差的排序是不合理的。不仅要考虑分段总误差对时间序列的影响,还要考虑分段所包含的时序长度对时间序列分段优先级的影响。对以往的时间序列重要点按照分段拟合误差比较的分段算法进行了改进,先将分段按照拟合误差大小进行排序,然后选取指定数的分段按照分段包含的点数由小到大进行排序。 (2)从之前先按照拟合误差排序,后按照分段包含的点数排列的优先级队列中,选取前两个分段,进行预处理,即模拟进行各自按照重要点分段之后,将分段之后的拟合误差与之前分段的拟合误差作比较,分段之后拟合误差减小的多的分段优先进行分段,表示采用该段进行分段之后,拟合误差会减小得更快,此方法考虑了分段的连续性,从而让拟合误差减小的多的分段优先分段。 (3)在进行模拟分段预处理和实际分段时,陈然[20]直接采用垂直距离最大的点将某一分段一分为二,然后逐一进行分段,分段的效率并不高,实际的重要点的分布经常是连续的,与具体的时间序列有关。如图3所示,时间序列片段x=1的点为最大值点,时间序列片段x=3的点为最小值点,分别为重要点,需要进行分段,使用固定点分段算法需要分段两次,才能同时找到x=1和x=3对应的点,如果能够一次同时获取两个分段点,将提高分段的效率。通过大量的数据观察测试发现,经常在某一段的最大值点或最小值分段之后,接下来就在该段的最小值点或最大值点进行分段,当某一分段中如果满足分段的原始曲线与拟合曲线的最大值与最小值符号相反并且或满足时,可以同时将最大值点与最小值点同时进行分段,从而一分为三,而不是一分为二,有效提升分段的效率。 图2 分段与时序长度的关系 图3 分段与拟合最大值和最小值的关系 PLR_TSIP算法执行流程如图4所示,具体描述如下:算法输入为时间序列X=(x1,x2,…,xi,…,xn)和固定分段数N或压缩率,算法输出为重要点集合IPs。 图4 PLR_TSIP算法执行流程 步骤1对时间序列数据X进行归一化处理,初始化分段点的集合IPs,将时间序列X的起点和终点加入到集合IPs中,将X的起点和终点构成的分段加入到优先级队列Q中。 步骤2计算优先级队列Q中新加入的分段拟合误差,优先级队列Q按照拟合误差的大小进行排序。 步骤3取出优先级队列Q中按照拟合误差排列的前k段(默认值为5),对前k段按照时间序列的分段长度进行从小到大排序。 步骤4选出步骤3中分段长度小的前两段,进行预处理,即模拟进行各自按照重要点分段之后,将分段之后的拟合误差与之前分段的拟合误差作比较,分段之后拟合误差减小较多的分段优先进行分段,将拟合误差减小的多的分段优先进行处理。 步骤5计算通过步骤4获取的分段的原始曲线与拟合曲线的最大值与最小值,如果满足符号相 反并且或时,可以同时将最大值点与最小值点作为分段点同时进行分段,从而一分为三,然后将分段起点,最大值点,最小值点,分段终点构成的三条时序分段,放到优先级队列Q中,同时固定分段点数N减2;否则按照重要点进行分段,将由分段的起点,重要点和分段终点构成的两条时序分段按照拟合误差由大到小的顺序加入到优先级队列中,同时分段点的个数N减1。如果分段点N的个数大于零,返回执行步骤2,当分段点的个数N为零时,就停止执行,输出重要点集合IPs。 基于重要点的时间序列固定点分段算法输入参数为时序数据集和压缩率,实验环境为:内存为8 GB的Intel电脑,开发语言采用Python。实验数据集采用IBM common stock closing prices:daily,29th June 1959 to 30th June 1960原始时间序列,时序长度为255和Keogh[3]等人提供的来自不同领域的公开数据集(简称KData数据集),KData数据集具有良好的广泛性和代表性,为方便对比,从KData数据集选取了其他论文中常用的11个作为实验数据,数据如表1所示。由于数据集中各个时间序列来自不同领域,序列值相差很大,所以为了便于计算和对比,在采用固定点分段算法之前首先需要对时间序列做[0,1]区间规范化处理,规范化公式如下: 表1 KData数据集描述 IBM common stock closing prices:daily,29th June 1959 to 30th June 1960原始时间序列长度为255,原始时间序列如图5所示,当选择的压缩段数为50时,拟合效果如图6所示,可以直观地看出,压缩后的序列很好地保留了总体的趋势。 图5 股票原时间序列 图6 股票数据线性拟合(50段) KData提供的Burst数据长度为9 382,原始时间序列如图7所示,当选择的压缩率为80%时,拟合结果如图8所示,可以直观地看出,压缩后的序列较好地反映了原序列的主题特征。 图7 原始Burst曲线(9 382段) 图8 Burst拟合曲线(1 876段) 算法的性能通过在同一压缩率下,比较分段线性表示序列与原序列的拟合误差的大小来确定。在相同压缩率为80%的情况下,比较PAA[7]、PLR_PF[22]、PLR_FPIP[20]、PLR_TSIP这四种算法的拟合误差,如表2所示。随着时间序列分段数的增加,PLR_TSIP方法的拟合误差明显小于PAA与PLR_PF,PLR_TSIP算法与PLR_FPIP算法相比,拟合误差的降幅最小为7%,最大为22%,平均为13%。 表2 80%压缩率下的拟合误差 比较PLR_TSIP、PLR_PF、PAA这三种算法选用Ocean数据集在不同压缩率情况下的拟合误差,如图9所示,随着时间序列分段数的增加,算法拟合误差在减小,但在相同压缩率的情况下,PLR_TSIP算法的拟合误差明显小于PAA、PLR_PF这两种算法。 图9 不同压缩率拟合误差比较1 比较PLR_TSIP与PLR_FPIP这两种算法选用Ocean数据集在不同压缩率情况下的拟合误差,如表3所示,随着时间序列固定分段数的增高,PLR_FPIP与PLR_TSIP的拟合误差都在减小,但PLR_TSIP的拟合误差要小于PLR_FPIP,PLR_TSIP算法与PLR_FPIP算法相比,拟合误差的平均降幅为15%,压缩率较小时甚至可以提高30%以上,非常明显。 表3 不同压缩率拟合误差比较2 PLR_TSIP算法的时间优化主要体现在步骤5,与陈然[20]的基于重要点的分段算法相比,时间优化主要体现在根据最大值Vimax与最小值Vimin的符号和大小关系可以在一次分段的同时得到两个分段点,而不需要经过两次分段,减少了分段的执行次数,从而提高了分段的效率,降低了算法的时间复杂度,下文通过实验加以证明。PLR_TSIP与PAA、PLR_PF相比,由于计算量大,因此执行时间较多,但拟合误差比PAA和PLR_PF降低很多。与同为重要点算法的PLR_FPIP相比,表3表明拟合效果提高很多,此处与PLR_FPIP进行时间效率比较,图10所示,相同分段数时,PLR_TSIP要比PLR_FPIP算法效率较高,性能平均可以提高20%以上。 图10 拟合时间比较 本文提出了一种基于重要点的时间序列的分段方法,避免了让用户输入拟合误差等难以确定的参数值,实验证明,这种方法在保留了原始时间序列的整体特征的基础上,减小了拟合误差,并提高了时间效率。在来自不同领域的公开数据集上的实验结果表明:与传统的PAA算法和其他主要的分段线性算法PLR_PF、PLR_FPIP相比,该算法具有很好的拟合效果和适应性。接下来将进一步研究参数的合理性,如文中k值选取为固定值5,同时也在对当前的算法进行改进,从而进一步减小拟合误差,提升算法效率。


2.2 时间序列重要点探测技术


2.3 问题分析


3 PLR_TSIP算法

4 实验与分析
4.1 数据集描述
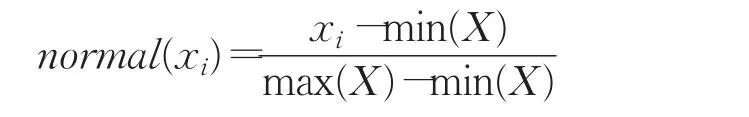

4.2 拟合结果



4.3 算法分段拟合误差比较



4.4 算法耗时分析与比较
5 结论


