一种SVDD增量学习淘汰算法
孔祥鑫,周 炜,王晓丹,于明秋
空军工程大学 防空反导学院,西安 710051
1 引言
支持向量数据描述[1](SVDD)是Tax和Duin等人提出的一种单分类算法。它使用同类样本数据建立一个最小超球体的数学模型,用来实现对原样本的描述和新样本的分类[2-4]。然而,在大多数情况下,难以在训练初期就获得某类样本完备的训练数据集,即训练样本是不断加入的。为满足准确率的要求,通常将新增样本加入原样本中一起进行训练并更新分类模型。SVDD构造超球体的实质[5]是求解一个二次规划问题,随着时间的累积,当样本量增大到一定程度时,会导致训练时间过长甚至无法进行。增量学习思想[6]不同于上文提到的整体块学习思想,它希望在模型更新时,仅保留历史模型中的有用信息,同时对新知识进行筛选,去除其中的冗余信息,从而提高模型的训练效率。
基于这一思想,许多学者进行了SVDD增量学习算法的研究。在已有研究中,文献[7]使用原样本集中的支持向量(Support Vector,SV)与增量样本中违反Karush-Kuhn-Tucker(KKT)条件的样本进行训练,但该算法无法控制增量学习过程中支持向量数量增加对模型更新时间的影响;文献[8]提出一种基于提升思想的SVDD增量学习方法,不断将误判样本提升为训练样本并更新分类器,直到分类效果满足某一阈值,但该算法可能会因更新次数过多而影响模型构建的效率,同时对于阈值如何设定,没有给出明确说明;文献[9]多次利用KKT条件对样本进行筛选,利用得到的少量样本进行训练,提升了模型的训练效率,但该方法实现增量的过程缺乏理论依据;文献[10]提出一种定向蚕食快速增量SVDD算法,使得增量SVDD的增长步长大于1,但是该方法依赖于初始训练集的选择,若选择不恰当,则会导致模型训练效率和分类精度大大降低。
本文提出了一种新的SVDD增量学习淘汰算法(NISVDD)。该算法在增量学习过程中考虑到了原样本中的非SV样本,以及满足KKT条件的增量样本中与原超球分类面距离较近的样本。通过设置自适应阈值并采用一种样本淘汰机制,充分挖掘含有重要分类信息的样本并及时淘汰对新模型构建影响不大的样本。实验结果表明,NISVDD算法在提升训练效率的同时,能够确保模型具有很高的分类精度。
2 SVDD相关理论
2.1 SVDD算法
SVDD算法对同类样本集合X={ }x1,x2,…,xN,先进行非线性映射Φ(xi),把xi映射到高维特征空间。然后,在特征空间中构造出一个包含训练样本的最小超球体。
对该问题描述如下:

其中O为球心;r为超球体半径;ζi和C分别是松弛变量和惩罚系数。
利用Lagrange乘子法构造Lagrange方程:

其中,ai≥0,μi≥0为Lagrange乘子。对式(2)中各变量求偏导,并令偏导数为0,将得到的结果代入式(2),可得到式(2)的对偶问题为:

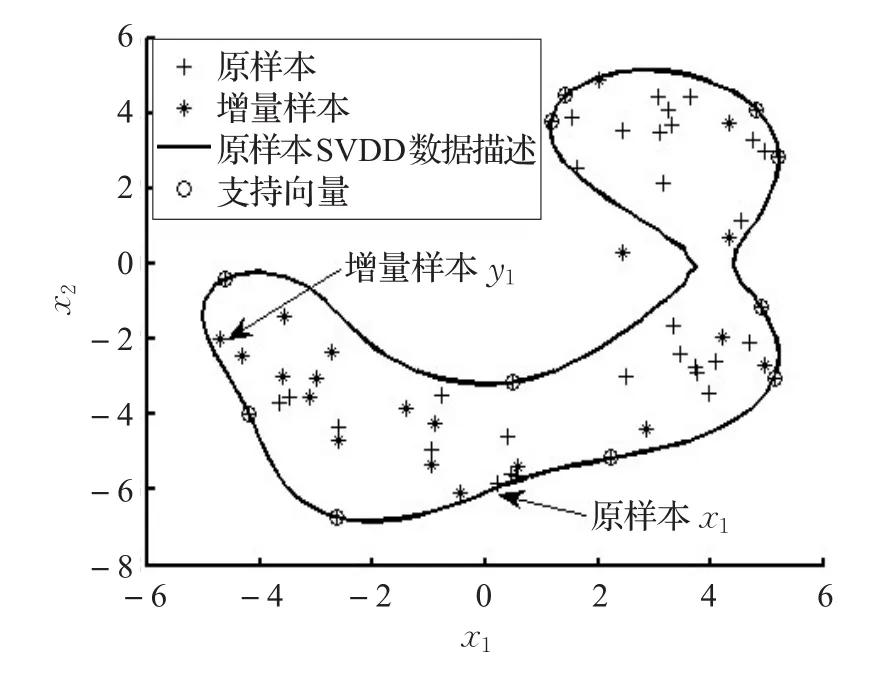
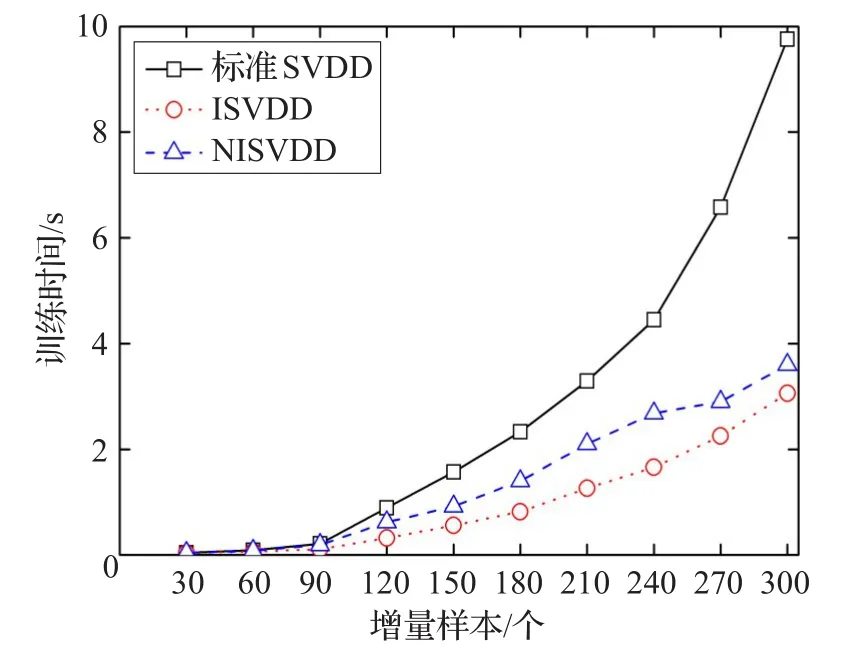
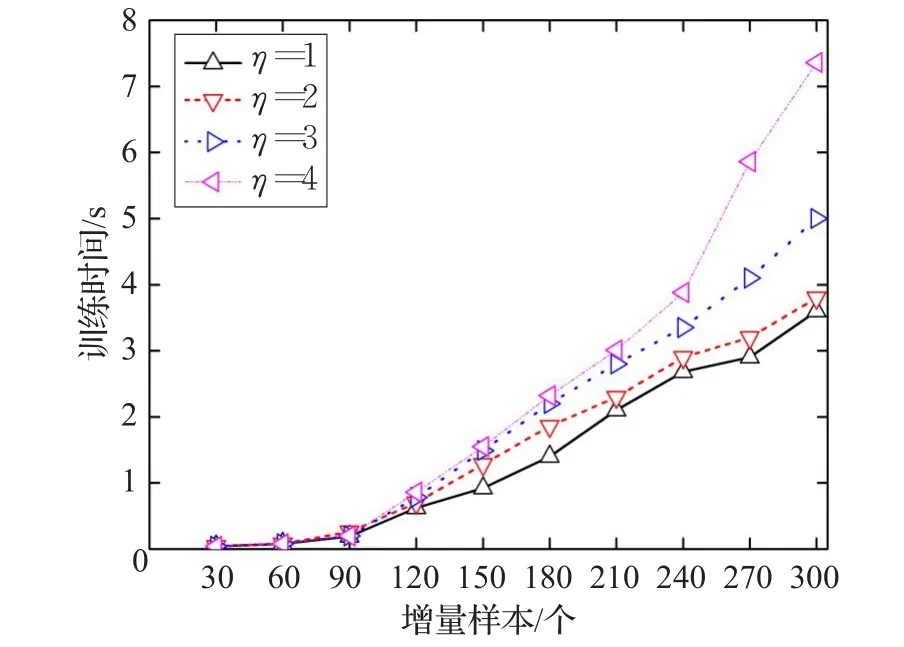
解该优化问题可得到ai,其中使得0 对待测样本Z,若满足式(5)条件,则被判为目标类,否则被判为非目标类: 由SVDD算法描述可以看出,构造超球的实质是求解一个二次优化问题,只有当所有的xi均满足下面的KKT条件时,[ ]α1,α2,…,αn才是规划问题的最优解。 其中,di2表示样本xi到球心距离的平方。在SVDD分类中,对应αi=0的样本位于超球内(含超球边界);对应0<αi 构建的SVDD模型由作为支持向量的样本决定,即支持向量集可以充分描述整个目标样本集的特征。基于此原理,当增量样本加入原样本后,使用可能成为新模型支持向量的样本集代替整个样本集进行训练,就能在保证分类精度的同时缩减训练时间。当已有的SVDD模型中加入新增样本时,会对应以下两类情况: (1)新增样本均满足原样本集的KKT条件,即新增样本均位于原超球内。此时,SVDD对合并后的样本集进行优化与对原样本集进行优化是等价的,新模型与原模型保持一致。 (2)新增样本集中存在违反原样本集KKT条件的样本,即新增样本中有部分样本位于原超球外。此时,原模型中样本间的平衡关系被打破,SVDD对合并后的样本集进行优化所得到的超球模型相比原模型会发生变形。常规增量算法(简称ISVDD算法)的做法是:仅保留原模型中的支持向量,将其与增量样本中违反KKT条件的样本一起训练,得到新的模型。 为研究在第二种情况下,原样本与新增样本中支持向量的具体变化情况,本文在MATLAB7.10编译平台上使用PR_tools工具箱并调用gendatb()函数生成两组Banana型数据集,分别包含40个和20个样本点。其中,40个样本点的数据集作为原样本集,另一组作为增量样本集。 首先,使用SVDD对原样本集构造数据描述,结果如图1。将新增样本加入原样本集,可以看出,新增样本中存在违反原样本集KKT条件的样本。 图1 对原样本集构造数据描述 然后,使用SVDD对包含60个样本的总样本集构造数据描述,结果如图2。 图2 对增量后的总样本集构造数据描述 可以看出,增量样本中违反KKT条件的样本成为了新的支持向量,大部分原支持向量也成为了新模型的支持向量。同时发现,若增量样本中存在违反原样本集KKT条件的样本,那么原样本集中靠近模型边界的非支持向量可能会成为新的支持向量,例如样本x1;增量样本集中靠近模型边界且符合原样本集KKT条件的样本也有可能转化为新的支持向量,例如样本y1。因此,ISVDD算法将这两类数据样本在SVDD增量学习过程中直接舍弃显然是不合适的,这会导致分类精度的降低。 为了从原模型的边界附近筛选出可能成为新模型支持向量的样本,定义自适应学习阈值α: 其中,r表示原模型的超球半径;ε为调节因子,可以表示为: 其中,xi是增量样本,函数 f(xi)返回增量样本xi到当前球心的距离;m是增量样本总数;count是计数函数,返回集合内的元素数量。ε的值等于增量样本中符合原模型KKT条件的样本数占增量样本总数的比例,反映了当前模型对该目标类样本描述的完备程度。 当加入增量样本后,计算得到阈值α,从原模型的非支持向量中筛选出距离球心大于阈值α的样本;同时,符合原样本KKT条件的增量样本,若其与球心的距离大于α,也会被筛选出来。这些筛选出的样本将组成新集合,与原模型的支持向量和违反原样本KKT条件的增量样本一起参与增量学习。 可以看出,阈值α的取值满足0≤α≤r,且阈值α具有自适应性:每次增量学习时计算得到一个对应的ε,ε值越小则表示当前模型越不完备,新模型与原模型相比将会发生较大变化,那么原模型边界附近的非支持向量和符合KKT条件的增量样本转化为新模型支持向量的可能性增大,此时阈值α随ε减小,能筛选出更多样本参与增量学习,有利于充分挖掘有用信息;反之,较大的ε值反映出模型在当前阶段对该目标类样本的描述较完备,那么原模型边界附近的非支持向量和符合KKT条件的增量样本转化为新模型支持向量的可能性变小,此时阈值α随ε增大,减少筛选出的样本数量,能有效避免对冗余样本的学习。特别的,当增量样本均符合原样本KKT条件时,阈值α=r,没有样本被筛选出来参与增量训练,新模型将与原模型保持一致。 随着增量学习次数的增加,整个样本集的规模不断扩大,模型边界附近的样本点也会越来越多。如果不对历史样本进行有选择的淘汰,那么随着增量学习的进行,通过阈值筛选出的样本将会非常多,从而严重影响增量学习的效率。 通过研究,发现如下规律:若某样本在多次增量学习得到的模型中,都是作为不影响边界形状的非支持向量,那么该样本在之后的学习中继续成为非支持向量的概率非常高。若及时将这类对后续学习影响较小的样本淘汰,就能提高增量学习的效率。基于此,提出一种样本淘汰机制: 首先,设定阈值η(η是正整数),对每个样本均设置一个计数器θ,初始化令θ均为0。在每次增量训练完成之后,对所有样本的θ值进行如下操作:如果该样本是模型的支持向量,则将其θ置0;反之,如果该样本是模型的非支持向量或未参与本次训练,则令其θ加1。在下一次增量训练之前,将满足θ>η对应的样本淘汰。 阈值η的选取没有唯一的标准,对于不同类型的目标样本,最佳的阈值η可能会不同。一般而言,当阈值η取值过大时,会保留大量的冗余数据,从而导致训练时间过长,达不到样本淘汰机制提高增量学习效率的目的;当阈值η取值过小时,会舍弃大量的有用信息,从而导致新模型的分类精度不高,无法体现出本文算法提升模型分类精度的优势。大量不同类型数据集上的实验结果表明,当阈值η在1~4范围内选取时,增量算法同时具有较快的训练速度和较高的模型分类精度。 综合以上思想,提出一种新的SVDD增量学习淘汰算法,其具体算法描述如下: 输入:原样本集X0及各样本的θ值,原SVDD模型Ω0,新增样本集X1,阈值η。 输出:增量学习后的模型Ω。 步骤1X0中支持向量样本组成集合SV0,剩余样本组成集合NSV0。 步骤2将SV0中所有样本的θ置0,同时令NSV0中所有样本的θ值加1。 步骤3检验X1中是否存在违反KKT条件的样本,若无,则输出Ω0,算法结束;否则,X1被分为违反Ω0的KKT条件的样本集X1v和符合Ω0的KKT条件的样本集X1s。 步骤4计算ε和α,根据样本淘汰机制,淘汰掉NSV0中θ>η的样本,将剩余样本组成集合NSV0′,从NSV0′和X1s中筛选出到球心距离大于阈值α的样本,放入样本集Xm。 步骤5将X1v,SV0和Xm合并,训练得到分类模型Ω 。将 NSV0′,X1v,X1s,SV0合并为样本集 X0,作为后续增量学习的原样本集。 为验证本文提出的NISVDD算法的性能,将NISVDD算法与标准SVDD算法和常规增量算法(ISVDD)进行比较,所有实验在Intel®CoreTMi7-4790 CPU@3.60GHz,Windows 7机器上完成,编译平台为MATLAB7.10,实验数据分别采用UCI数据集和弹头目标HRRP数据集。 本文所选UCI数据集为breast-cancer数据集,该数据集来自美国Wisconsin州医学院记录的关于乳腺癌的真实临床数据。该数据集共包含699条维度为11的数据,第1列是病人ID,第2列是分类标识(2表示良性,共458条;4表示恶性,共241条),其余9列是判断乳腺癌的9个属性。 图3给出了标准SVDD、ISVDD和NISVDD(η=1)对增量数据的训练时间。可以看出,NISVDD算法的训练时间接近ISVDD,但远小于标准SVDD算法。主要原因是:标准SVDD算法在每次增量学习时必须要对新增样本和所有历史样本全部重新训练,没能提取有效的历史信息,大量的重复训练导致其训练时间过长;ISVDD只保留前一次学习得到的支持向量样本与增量样本合并进行训练,因此训练时间最短;本文提出的NISVDD算法参考前几次的学习结果,可以对历史样本进行有选择的保留和淘汰,因此训练时间也较短。 图3 breast-cancer数据集的训练时间 图4 给出了 η分别取1,2,3,4时,NISVDD算法对增量数据的训练时间。可以看出,当η取值增大时,NISVDD的训练时间也随之增加,但均小于标准SVDD算法。主要原因是:η是控制样本淘汰的速度的一个参数,η的增大使得样本淘汰的速度和数量下降,从而使训练时间增加。 图4 η不同取值时的训练时间 在上述增量训练过程中,用剩余的158条良性数据作为测试样本集,分别检验增量学习各阶段所得模型的分类性能。 图5给出了3种算法的分类精度,可以看出,3种算法在训练初期的分类精度相近,但随着增量学习过程的深入,标准SVDD算法和NISVDD算法的分类精度均逐渐增高且两者分类精度相差较小;而ISVDD算法分类精度增加的幅度较小,甚至不随新样本的加入而增大,其分类精度在增量学习后期明显小于其他两种算法。主要原因是:ISVDD算法在增量学习中过多追求样本量的缩减从而导致大量对模型构造有用的样本被舍弃,使其分类精度下降;而NISVDD算法在进行样本缩减的同时,采取了必要机制防止包含有用信息样本的丢失,因此其具备和标准SVDD算法相近的分类精度。 图5 不同算法对breast-cancer数据集的分类精度 图6 给出了 η分别取1,2,3,4时,NISVDD算法的分类精度。可以看出,不同取值对应的分类精度在增量学习各阶段的变化趋势相近,当取较大值时,分类精度会有所增加。主要原因是:η的增大使得样本淘汰的标准更加严格,可能包含有用信息的样本被保留的时间更长,分类精度也随之增大。 图6 η不同值对breast-cancer数据集的分类精度 从以上实验结果可以看出,应用NISVDD算法进行增量学习时,在提升训练效率方面具有和ISVDD相近的优势,并且能够保持和标准SVDD相近的高分类精度。增大阈值η可以获得更高的分类精度,但会降低训练速度;减小阈值η可以提升模型的构建效率,但会损失分类精度。 结合图4和图6可以看出,与η=1相比,η=2时模型的分类精度提升很明显,但两者的训练速度接近;与η=3、η=4相比,η=2在分类精度方面的损失非常小,但在训练速度上却明显占优。因此,对于breast-cancer数据集,当阈值取η=2时,NISVDD算法可以很好地平衡分类精度与训练效率,使增量学习的整体效果达到最优。 当雷达距离分辨单元远小于目标的径向尺寸时,目标会连续占据多个距离单元,从而在雷达视线投影上形成目标幅度的图像,称为目标高分辨一维距离像(High Range Resolution Profile,HRRP)[12]。实验使用 FEKO电磁计算软件生成弹头目标的HRRP数据[13]。设置雷达入射波方位角范围为0°~180°,间隔为0.05°,雷达带宽为1GHz,频率范围为8.5~9.5 GHz,频点数为128,频率步进7.874 MHz。得到弹头目标的全方位样本集包含3 600个数据,在实验中选择每15°作为一个实验范围,则该角域包含300个样本,选择其中180个样本作为整个训练样本集,剩下的120个样本作为测试样本集。提取HRRP样本的幅度谱差分特征[14]、能量聚集区长度特征[15],采用PCA算法对幅度谱差分特征进行降维,得到5维的特征数据,把其与能量聚集区长度特征进行组合得到6维的弹头目标HRRP样本特征数据。 为模拟雷达持续获取弹头目标信息的情形,将训练样本集划分为8个样本子集,其中第一个子集包含40个样本,作为雷达t0时刻录入的初始样本集;其余7个子集均包含20个样本,分别在t1~t7时刻依次录入。不断更新训练模型并测试分类精度,具体参数设置方法与5.1节中实验相同。 图7为标准SVDD、ISVDD和NISVDD(η=1)对弹头目标HRRP样本进行增量学习过程中的训练时间,图8为 η分别取1,2,3,4时,NISVDD算法对增量数据的训练时间,图9为几种算法在各时刻所得模型的分类精度,图10为 η 分别取1,2,3,4时,NISVDD算法的分类精度。 图7 弹头目标HRRP数据的训练时间 可以看出,几种算法在弹头目标HRRP数据上的实验结果与在breast-cancer数据集上的实验结果大体一致。不同之处在于,当阈值取η=3时,与η=1、η=2相比,能够在训练时间增加较少的同时使模型的分类精度明显提升;与η=4相比,两者的分类精度相近,但η=3时的训练速度更快。因此,当阈值取η=3时,NISVDD算法在弹头目标HRRP数据上的整体性能最佳,不仅能够随着弹头目标HRRP数据的不断获取快速更新分类模型,而且能够保证较高的分类精度,符合弹头目标识别所需的快速性、准确性的要求。 图8 η不同取值时的训练时间 图9 不同算法对弹头目标HRRP数据的分类精度 图10 η不同值对弹头目标HRRP数据的分类精度 本文提出了一种新的SVDD增量学习淘汰算法,通过定义自适应学习阈值筛选出潜在的支持向量,提高了增量学习的精度;通过一种样本淘汰机制及时淘汰包含冗余信息的样本,提升了模型的训练效率。在UCI数据集上的实验结果证明了本文方法的正确性与有效性。同时,本文方法对弹头目标HRRP数据也表现出很好的适用性,这有利于将NISVDD算法应用于弹头目标在线识别领域。对于NISVDD算法的后续改进,可以进一步研究如何根据已有的样本信息,在增量学习之前确定出可能的最佳淘汰阈值η,从而进一步提高SVDD增量学习的整体性能。

2.2 Karush-Kuhn-Tucher(KKT)条件

3 SVDD增量理论分析

4 一种新的SVDD增量学习淘汰算法(NISVDD)
4.1 自适应学习阈值


4.2 样本淘汰机制
4.3 NISVDD算法描述
5 实验分析
5.1 UCI数据集
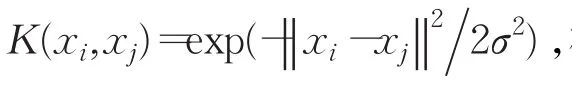


5.2 弹头仿真HRRP数据




6 结束语

