改进SMOTE的非平衡数据集分类算法研究

赵清华，张艺豪，马建芬，段倩倩

太原理工大学 信息工程学院&新型传感器和智能控制教育部（山西）重点实验室 微纳系统研究中心，太原 030600

1 引言

随机森林通过自助采样[1]获得数据子集构建决策树得到很好的分类预测效果，被广泛应用于数据挖掘各个领域中。在数据挖掘实际应用中，数据采集后的数据集样本通常是不平衡的。所谓不平衡样本数据集是指某一类的样本数量明显少于另一类样本数量，在二分类问题中，数量占优势的类别通常称为负类或多数类，数量稀少的分类通常称为正类或少数类。Weiss通过大量实验总结了不平衡数据集异常点、噪声和某一类样本数量稀少等问题[2]，得出了随机森林分类器在分类预测不平衡数据集时，结果倾向于多数类，造成很大的预测误差。实际数据集如癌症诊断、血液样本中心、网络信息安全等数据集通常是不平衡的，所以如何改进传统算法解决数据集不平衡分类问题是机器学习与大数据挖掘的研究热点。

Chawla等人以随机向上抽样为核心思想提出了SMOTE算法[3]，通过人为构造正类样本使得数据集中负类样本和正类样本的数量趋于平衡。文献[4]中提出一种基于SVM调参的算法来处理不平衡数据集，性能较SVM算法有所提升。吴洪兴在文献[5]中提出将遗传算法的遗传算子与支持向量机算法进行组合，较好地解决了支持向量机倾向性预测问题。针对文献[3]，文献[6]提出了一种将boost机器学习思想与样本构造结合起来，对原始正类样本中错误分类的样本加大权值，将训练的许多弱分类器组合成强分类器，减少了对正类样本的预测误差。文献[7]中提出代价敏感学习算法，其核心思想是赋予正类样本错判更大的惩罚。正类较负类错判代价高迫使模型对稀少的正类具有更高的预测正确率[8]。文献[3]无法控制正类样本生成区域和样本生成个数，样本分布容易边缘化。文献[4-7]采用增加模型正类样本的权值，加大误判惩罚的方法处理问题，算法计算复杂度大，时间效率较低。

综上所述，目前多数算法优化研究重点关注正类样本的权重与误判惩罚两个方面，在算法复杂度，数据集分布等方面研究力度不足。本文从限制样本生成区域着手，提出两种改进算法，TSMOTE算法和MDSMOTE算法。改进算法与随机森林的组合模型在6种不平衡数据集上进行大量仿真实验，实验结果表明改进算法进一步提高了随机森林在不平衡数据集上G-mean值、F-value值和AUC值，同时减少了算法时间复杂度。

2 传统算法与原理

2.1 随机森林

随机森林是一种性能较好，预测分类准确率较高的组合分类器，是Bagging集成机器学习方法中最典型的算法[9]。随机森林模型在构造的时候具有两个随机性。第一个随机性是采用自助采样法从样本数据集随机有放回地采样，构造出n个数据子集。第二个随机性是运用上一步得到的n个数据子集进行n个决策树模型的构建[10]。随机森林构建决策树模型时随机选择若干个属性，然后选择最佳属性作为分裂节点。决策树对分类任务采用简单投票法决定最终分类的类别。以上所述的两个随机性使得随机森林很好地避免了一般决策树所具有的过拟合问题，很好地提高了预测分类准确率。定义样本集A={(Xi,Yi),i=1,2,…,n}，每个样本有d个属性，决策树数目为N。随机森林算法详细步骤如下：

算法1随机森林

输入：样本集A={(Xi,Yi),i=1,2,…,n}，每个样本d个属性，待测样本Xtest。

1.Forj=1,2,…,N，训练集自助采样生成数据子集Si(i=1,2,…,N)。

2.选择数据子集Si作为构造第i个决策树的样本集合。

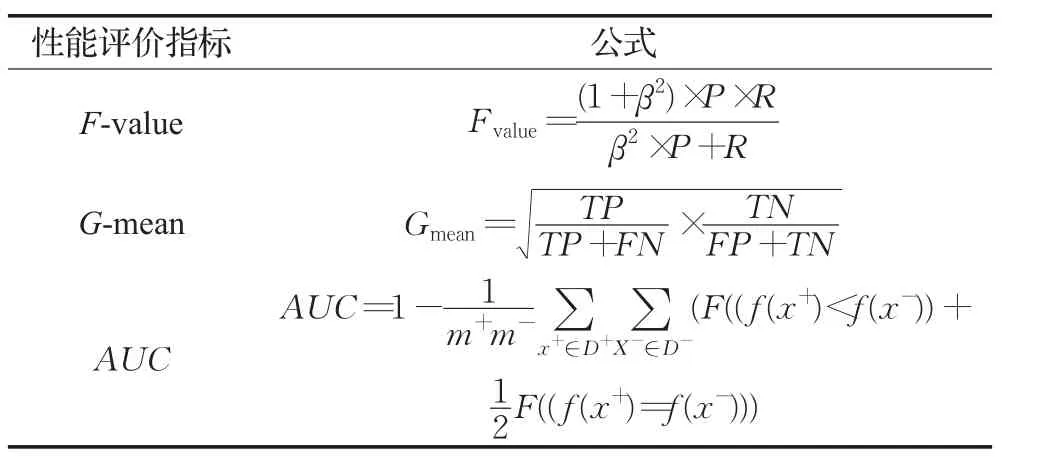
3.样本d个属性中随机选择m(m

4.选择信息熵增益率最大的属性作为分裂结点进行决策树的分裂，总共得到N个决策树。

5.对于待测样本Xtest，决策树ti输出为ti(Xtest)，随机森林分类输出为

2.2 SMOTE算法

SMOTE算法是先根据欧几里德距离将正类样本进行分组，假设一个样本X为X={x1,x2,…,xn},x1,x2,…,xn为样本X的n个维度值。同理样本Y={y1,y2,…,yn}。那么样本X与样本Y的欧几里德距离D为：

欧几里德距离最近的6个样本分为一组。根据聚类的思想[11]，正类样本在空间上距离较近的样本也是正类。SMOTE算法在每组6个样本中，样本两两之间连线上随机人为构造新的正类样本。

其中i=1,2,…,6,X表示稀少正类样本，Yi为X的第i个近邻样本，rand(0,1)表示0到1的一个随机数。Xnew表示新生成的样本。根据公式（2）进行多次迭代使得数据集平衡。SMOTE算法详细步骤如下：

算法2 SMOTE算法

输入：正类样本集Xpositive，负类样本集Xnegative。

1.对正类样本集Xpositive进行分组，欧几里德距离最近的6个样本分为一组。

2.每组样本两两之间连线上根据公式（2）随机生成正类样本，加入数据集。

3.While (Xpositive:Xnegative不等于1)

执行步骤2

END

随机森林与SMOTE算法组合较好地改善了分类结果倾向性的问题，使得模型对正类样本的分类预测正确率有所提高。SMOTE不能解决数据集存在的样本边缘化问题且算法时间复杂度大。本文改进数据集自身分布的方法，克服上述算法的不足。

3 不平衡数据集分类算法的改进

3.1 三角质心TSMOTE算法

SMOTE算法存在两个明显不足，无法解决数据集正类样本分布的边缘化问题[12]，计算复杂度大。本文针对其不足首先提出了TSMOTE（Triangle SMOTE）算法。TSMOTE算法重点关注新样本产生的区域，避免新样本使得数据集分布进一步边缘化。TSMOTE算法首先将样本集进行分组，每6个样本为一组。然后在每组随机抽出3个样本如X1,X2,X3,Xi={Xi1,Xi2,…,Xin}。计算出3个样本的质心XT为：

3个样本组成三角形，样本本身为三角形的顶点。每个顶点与质心的连线上随机产生一个正类样本，一个三角形产生3个新的正类样本。新样本向质心靠拢，较好地改善了SMOTE算法新样本分布进一步边缘化的问题。每组新样本的产生区域有一定的限制，新样本好比受着引力的影响靠拢着质心。TSMOTE算法详细步骤如下：

算法3 TSMOTE算法

输入：正类样本集Xpositive，负类样本集Xnegative。

1.对正类样本集Xpositive进行分组，欧几里德距离最近的6个样本分为一组。

2.每组随机抽取3个样本点作为三角形顶点，依据公式（3）计算质心。

3.三角顶点与质心连线之间随机产生新的样本。

4.While (Xpositive:Xnegative不等于1)

执行步骤3

END

3.2 最远点MDSMOTE算法

TSMOTE算法较好地限制了新样本产生的区域，改善了样本数据集分布问题，计算复杂度仍然较高。实际应用中，样本点一般是空间多维度，针对上百、上千甚至上万维度，SOMTE算法、TSMOTE算法消耗时间会大幅增加。本文针对这个不足进一步提出MDSMOTE（Max Disatance SMOTE）算法。该算法只关注两个样本点，正类样本质心点和距离质心最远的正类样本点。在最远点和质心点连线之间随机产生新样本点：

Xnew为新样本点，Xc为所有样本的质心点，Xmax为距离质心点最远的正类样本点。该算法首先摒弃了传统SMOTE算法将正类样本点分组的思想，只关注正类样本质心点和距离样本质心点最远距离的样本点，大大减轻了算法复杂度。而且MDSMOTE算法只需要迭代一次，根据公式（4）产生一批新样本点直接使得整个数据集样本达到平衡，算法简单易实现。其算法详细步骤如下：

算法4 MDSMOTE算法

输入：正类样本集Xpositive，负类样本集Xnegative。

1.计算正类样本的质心，遍历所有正类样本找出距离质心最远的样本点。

2.质心与最远点连线之间依据公式（4）一次成生大量正类样本使得样本数据集平衡。

4 实验结果与分析

实验中采用不平衡数据集常用的F-value、G-mean和AUC这3个指标来评价分类算法的优劣，这3个指标都是以混淆矩阵为基础扩展的[13]，混淆矩阵定义如表1所示，表2给出了3个指标的计算公式。

表1 二分类的混淆矩阵

表2 评价标准的计算方法

TP、FN分别为真实类别为正类，预测结果为正类、负类的数目。FP、TN分别为真实类别为负类，预测结果为正类，负类的数目。查准率P与查全率R分别定义为：

其中，F-value综合评价查全率与查准率，能很好评价模型对稀少样本类的分类效果[14]，式中β=1时，F-value为查准率和查全率的调和平均数[15]。β＞1时，查全率有更大的影响，β<1时，查准率有更大的影响。G-mean值综合考察正类预测分类准确率和负类预测准确率，只有正类预测正确率与负类预测正确率都高的时候，G-mean值才会增加。AUC式中，m+、m-为正例和反例个数，D+、D-分别表示正例集合和反例集合。f(x+)表示判别为正类样本的概率，F(x)为指示函数，x为真时，F(x)值为1。正例的预测值比反例预测值小，给予模型值为1的惩罚。正例的预测值等于反例的预测值模型给予值为0.5的惩罚。对于不平衡数据集，AUC值越大模型分类效果越好。

4.1 实验环境设置

为了检验文中改进算法的有效性与普适性，本实验采用表3所示6组不平衡数据集作为检验集，采用Python语言，Jupyter notebook编程环境对改进算法进行仿真实验。这6组不平衡数据集分别为血液捐助中心、糖尿病患者、酵母菌、汽车保险索赔、图片分类和玻璃辨识数据集，其中酵母菌数据集不平衡率尤为突出。

表3 不平衡数据集特征与分布

每次实验随机划分80%为训练集，20%为测试集；随机森林中用于生成随机数发生器的种子置0；SMOTE算法与TSMOTE算法需要分组，设定每组的样本均为6个；TSMOTE算法组内每次随机抽取3个样本用于构造新样本；实验评价指标F-value和G-mean是在随机森林的决策树个数为10时仿真100次求平均值来得到；为了更好地比较算法的计算复杂度和所消耗的时间，评价指标AUC值和实验耗时是在特意仿真1 000次求平均得到的。

4.2 实验结果分析

表4为6组不同数据集上3种算法的G-mean指标比较，决策树个数均设置为10，可以看出，6组样本集中SMOTE、TSMOTE和MDSMOTE算法的G-mean值均逐渐增加，其中，TSMOTE算法的G-mean指标较SMOTE算法大幅度提升，MDSMOTE算法的G-mean指标较TSMOTE算法小幅度提升。血液数据集中SMOTE算法的G-mean指标只有0.563 1，TSMOTE算法的G-mean指标达到0.761 4，MDSMOTE算法的G-mean指标达到0.831 0，说明血液数据集中正类样本存在严重边缘化，导致SMOTE算法表现较差。改进算法限制区域的思想使得样本中正类样本没有边缘化，而是围绕着质心中心化，更好地改善了样本数据集分布，提高了分类器的性能。图1给出3种算法在随机选取的3组样本集（酵母菌、糖尿病和图片数据集）上随着决策树个数不同的G-mean指标，可以看出，3种算法的G-mean值均随着决策树个数增加而有所增加，并最终趋于平稳。在各个决策树参数上，本文改进的TSMOTE算法和MDSMOTE算法的G-mean指标均比传统SMOTE算法大幅度提高，综合比较，MDSMOTE算法表现最佳，平稳值是模型的最佳表现，继续增加决策树参数模型会因为过拟合而性能下降。

表4 不同算法上的G-mean指标结果

图1 3种算法在酵母菌、糖尿病和图片数据集上随着决策树个数不同的G-mean比较

表5和图2仿真得出算法的F-value指标比较，由表5可以看出，除了血液数据集，其他数据集上TSMOTE算法的F-value指标均得到提高。MDSMOTE算法的F-value指标在TSMOTE算法的基础上进一步提高，说明改进算法对正类和负类样本的预测准确率都有所提高。图2是3种算法在酵母菌、糖尿病和图片数据集上随着决策树个数不同的F-value比较，每种算法的F-value指标均随着决策树参数增加而增加。当决策树为3时，糖尿病数据集上SMOTE算法的F-value约为0.75，MDSMOTE算法的F-value约为0.78，性能提升较小，而对于酵母菌和图片数据集，SMOTE算法的F-value分别约为0.72和0.87，MDSMOTE算法的F-value约为0.95和0.97，性能大幅度提高。究其原因可知糖尿病数据集本身边缘样本较少，所以采用中心化思想优化算法TSMOTE和MDSMOTE算法性能提升较小，而对于酵母菌和图片数据集边缘样本较多，性能大幅提升，F-value均在0.95以上。

表5 不同算法上的F-value指标结果

图3为算法复杂度对比实验结果，随机选取汽车保险数据集作为样本集仿真运行1 000次计算AUC指标，由图3（a）可知SMOTE算法 AUC值大多集中0.67左右，算法消耗时间44.7 s。由图3（b）可知TSMOTE算法 AUC值大多位于0.92左右，算法消耗时间39.3 s。由图3（c）MDSMOTE算法AUC值大多集中于0.935左右，算法消耗时间30.9 s。AUC值越大，说明模型对正类、负类的分类性能越好。显然，改进算法TSMOTE和MDSMOTE的性能都优于传统算法SMOTE。由图3（d）也可以看出在6种数据集上，SMOTE、TSMOTE和MDSMOTE算法消耗时间逐渐减少，SMOTE算法遍历所有正类样本，分组然后组内成生新样本时间复杂度为O(n2)，TSMOTE相当于减少组内用来生成新样本的原始正类样本，时间复杂度为O(0.2n2)，MDSMOTE算法不采用分组直接生成样本时间复杂度为O(n)。针对AUC指标实验数据集规模较小，数据集维度较小，实际数据挖掘应用中数据样本规模一般为十万、百万甚至更多，数据维度一般成千上万，算法计算量呈指数型增长，本文针对减少算法时间复杂度提出的两种算法在实际大规模数据集，海量样本数据挖掘工程中可以有效减少工程时间，提高数据挖掘工程效率。

图2 3种算法在酵母菌、糖尿病和图片数据集上随着决策树个数不同的F-value比较

图3 时间复杂度对比实验

5 结束语

由于随机森林和SMOTE算法组合存在样本边缘化、算法时间复杂度大的不足，本文提出了两种基于SMOTE的改进算法TSMOTE和MDSMOTE。改进算法将产生的新样本限制在一定区域中，使得模型对正类样本，负类样本的综合分类准确率提升，改善了SMOTE算法样本分布边缘化的问题。实验结果表明TSMOTE和MDSMOTE算法较SMOTE算法取得了较高的G-mean值、F-value值和AUC值，减小了算法时间复杂度，对于海量样本实际数据挖掘工程中可以有效减少工程时间，提高数据挖掘工程效率，进一步提高了对于不平衡数据集的综合分类性能。本文改进算法模型依然存在不少噪声样本，未来研究着重考虑将欠采样技术与重采样技术结合，使用过采样技术使得数据集平衡，然后使用特定的欠采样算法剔除样本集中的噪声样本和异常点，进一步优化模型。