基于余弦代价函数T/4分数间隔盲均衡算法—Simulink仿真

崔鹏鹏，韩迎鸽，李保坤，王 超

安徽理工大学 电气与信息工程学院，安徽 淮南 232001

1 引言

在数字通信系统中，有限的信道带宽、多径传播和非线性效应等因素引起的码间干扰（Inter Symbol Interference，ISI）会导致接收数据的误码[1]，严重影响通信质量。为了有效地消除这些不利因素的影响，可以在接收端采用无需发送训练序列的盲均衡技术[2]。在各种盲均衡算法中，常模算法（Constant Modulus Algorithm，CMA），因其结构简单、性能稳定而得到广泛应用[3]。CMA对高阶QAM信号，收敛较慢，收敛后稳态均方误差较大。相对于传统的基于波特间隔的常模算法，分数间隔常模算法[4]（Fractionally Spaced Equalizer based on Constant Modulus Algorithm，FSE-CMA）能够有效补偿信道畸变，提高系统的有效性[5]。但由于FSE-CMA的均衡器的权向量系数更新仍然采用的是CMA的代价函数进行调整，因此，对于非常模QAM信号，其稳态均方误差仍然相对较大，收敛速度仍然相对较慢。

本文针对非常模QAM信号，提出一种基于余弦代价函数的T/4分数间隔的盲均衡新算法（T/4 Fractionally Spaced Equalizer based on Cosine Cost Function，T/4-FSE-CCF），通过MATLAB的 M 文件对T/4-FSE-CCF的性能进行验证，并获取仿真相关的参数；在此基础上，搭建T/4-FSE-CCF的Simulink仿真模型。

2 T/4分数间隔常模盲均衡算法

图1给出T/4分数间隔均衡器[6-9]的结构图。

图1 T/4-FSE信道模型

图1 中，假设输入信号向量：

h(c)(k)是第c个子信道系统冲击响应，长度为N（N 为正整数）(c=0、1、2、3)

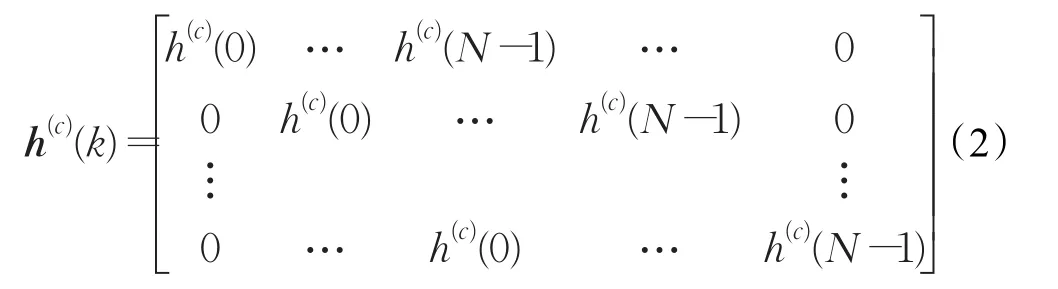
n(c)(k)是第c个子信道输入噪声向量：

x(c)(k)是第c个子均衡器输入信号向量：

f(c)(k)是第c个子均衡器抽头系数向量且长度为L（L为正整数）：

由图1，第 c条支路 (c=0、1、2、3)的物理量存在关系如下(M=4)：

式（6）中，h为整个系统的信道。

均衡器第c条支路的输入信号向量为：

均衡器第c条支路的输出为：

由于CMA的代价函数为：

式（9）中，R是信源s(k)的统计模值，且

采用最速下降法对第c个子均衡器权系数向量进行更新，以最小化式（9），得更新公式为：

为了便于理解和计算，利用矩阵表示均衡器的输入和输出：

该算法的误差函数项表达式为：

称式（1）～（13）构成的算法为T/4分数间隔常模盲均衡算法（T/4 Fractionally Spaced Equalizer based on Constant Modulus Algorithm，T/4-FSE-CMA）。

由代价函数式（9）可知，CMA目的是期望每个输出信号的幅度模值平方等于R，即，此时代价函数最小化为零，权系数向量稳定，但是对于非常模QAM信号，如16-QAM信号[10-13]，星座点坐标为s(k)=，所对应的幅度模值的平方值，根据式子（10）得 R=13.2，

3 基于余弦代价函数T/4分数间隔盲均衡算法

针对M-QAM(M＞4)信号，为了进一步提高T/4-FSE-CMA的性能，仿照CMA的代价函数，将式（9）修正为：

式中，yr(k)和 yi(k)分别为均衡器输出y(k)的实部和虚部。

该代价函数的目的是迫使均衡器输出信号y(k)的实部和虚部的余弦函数 cos2[yr(k)⋅π/2]和cos2[yi(k)⋅π/2]与统计模值R1和R2相等。

统计模值R1和R2的定义式为：

式（14）中，sr(k)和si(k)分别是信源s(k)的实部和虚部，当信号为M-QAM（星座的坐标为时，显然，M-QAM信号源星座坐标点使得cos[sr(k)⋅，此时，统计模值 R1和 R2恒等于零，因此，针对M-QAM非常模信号，进一步可将代价函数式（14）简化并降低阶数得到：

在最速下降法下，均衡器权向量更新公式为：

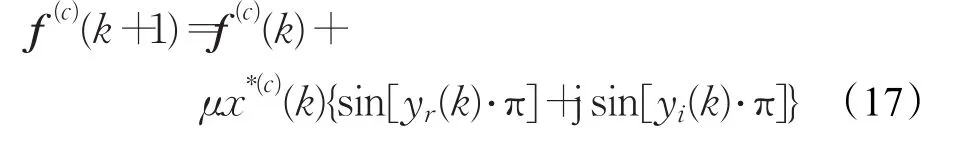
定义该算法的误差函数项表达式为：

将式（1）～（8）、（16）～（18）构成的算法定义为基于余弦代价函数T/4分数间隔盲均衡算法（T/4-FSE-CCF），由式（16）可知，基于余弦的代价函数摆脱了对统计模值R的依赖，且均衡器理想均衡时该算法的代价函数为零，均衡器抽头系数停止更新，稳态均方误差（Mean Square Error，MSE）为零。

4 Simulink建模与仿真

Simulink是MATLAB提供的一种可视化仿真建模库，可以使用库中已经存在的模块搭建所需的系统，点击运行之后，也可以显示出建模仿真的结果。与MATLAB的M文件仿真模型相比，Simulink搭建的模型直观清晰，更适于向硬件平台转移[7]。

4.1 M文件程序仿真

为了验证T/4-FSE-CMA和T/4-FSE-CCF的有效性，同时取得合适的Simulink仿真参数，现对T/4-FSECMA和T/4-FSE-CCF在MATLAB中先用M文件仿真。发射信号均为非常模16QAM信号，信噪比均为25dB，步长分别为和信道参数均为h=[0.965 6 0.090 6 0.057 8 0.236 8]，各子均衡器抽头个数均为10，且均采用中心抽头初始化，M文件的仿真结果，如图2所示。

（a）两种算法稳态均方误差曲线

图2MATLAB的M文件仿真结果

图2 （a）表明，T/4-FSE-CCF的稳态均方误差比T/4-FSE-CMA小了6 dB，收敛速度快了1 000步，图2（b）和图2（c）表明T/4-FSE-CCF输出的星座图更为紧密清晰，也就是说与T/4-FSE-CMA相比，T/4-FSE-CCF具有更快的收敛速度和更小的稳态误差。

4.2 基于余弦代价函数T/4分数间隔盲均衡系统设计

基于余弦代价函数T/4分数间隔的盲均衡（T/4-FSE-CCF）系统Simulink仿真模型是在传统的CMA盲均衡系统Simulink仿真模型[1]的基础上改进得来的，先介绍CMA系统仿真模型。CMA系统仿真模型如图3所示，由于CMA盲均衡系统的所有模块在Simulink模块库都有，从Simulink模块库[15]中找到如图3所示的各个模块，然后依次连接好各模块即可。

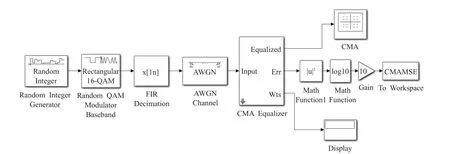
图3 CMA系统仿真模型

图4 T/4-FSE-CCF系统仿真模型

图5 CMA模块内部结构

由图3的CMA系统仿真模型可知，最左侧是随机整数信号发生器（Random Integer Generator），经过QAM正交幅度调制，输出发射信号序列，经一路子信道（FIR Decimation），一路噪声（AWGN Channel），传至CMA均衡器（CMA Equalizer），由图1可知，T/4-FSECCF为多信道系统。所以，在CMA系统仿真模型的基础上，需要变为4路子信道，4路噪声，有4个输入端的T/4-FSE-CCF均衡器，因此在图3基础上设计出T/4-FSECCF系统的Simulink仿真模型，如图4所示。从Simulink模块库中依次找到相应模块，并连接好。由于Simulink模块库只有CMA均衡器（CMA Equalizer），因此需要对其内部结构进行改造。

为了构造T/4-FSE-CCF系统，在接收端需将每一路子信号分别进行均衡，由于CMA均衡器（CMA Equalizer）只有一个输入，如图3。因此要对CMA均衡器模块进行改进使其变为4输入多信道的T/4-FSE-CCF均衡器。需要在CMA均衡器模块中增加3路信道，变成4信道系统。鼠标右击CMA均衡器模块（CMA Equalizer），选择Look under mask选项，得到图5的CMA均衡器内部结构。

为了变成4通道系统，在CMA均衡器内部结构中增加3路输入，即仿照图5，将各个子模块全部复制即可，最终得到图6。图6中，4路输入信号，分别进入4个子均衡器（Subsystem），每个子均衡器都有均衡输出、误差输出、权向量输出，并将各输出信号叠加然后取平均值，可得整个T/4-FSE-CCF均衡器的输出。

如图5搭建好模型后，接下来修改误差函数项，在图6中，单击每一个子系统模块（Subsystem），会出现CMA权向量更新子模块，依据式（18），将其中常模算法的误差项函数修改为余弦代价函数的误差项，修改后结果如图7所示。图7实线框内就是依据式（18）修改的余弦代价函数的误差项，修改完成后，关掉改造好的T/4-FSE-CCF内部结构，则会出现新的封装好的有4个输入端口的基于余弦代价函数的T/4分数间隔均衡器模块，即图4中的T/4-FSE-CCF均衡（T/4-FSE-CCF Equalizer）。

根据M文件仿真后所确定的参数进行Simulink仿真，T/4-FSE-CCF的Simulink仿真模型所得的仿真结果如图8所示，由于Simulink只能实现一次蒙特卡洛仿真，所以均方误差曲线比较粗。

Simulink模型在仿真的过程中，可以明显看到星座图的输出信号从发散到聚拢，星座图上的点在不停地变换，最后完成均衡，由图8（b）可以看出，在Simulink环境下，T/4-FSE-CCF系统输出的星座图紧密清晰，与M文件仿真得到的效果相同。

5 结束语

图6 T/4-FSE-CCF模块内部结构

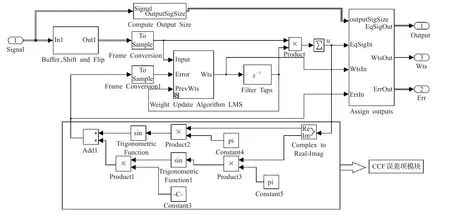
图7 CCF权向量更新子模块

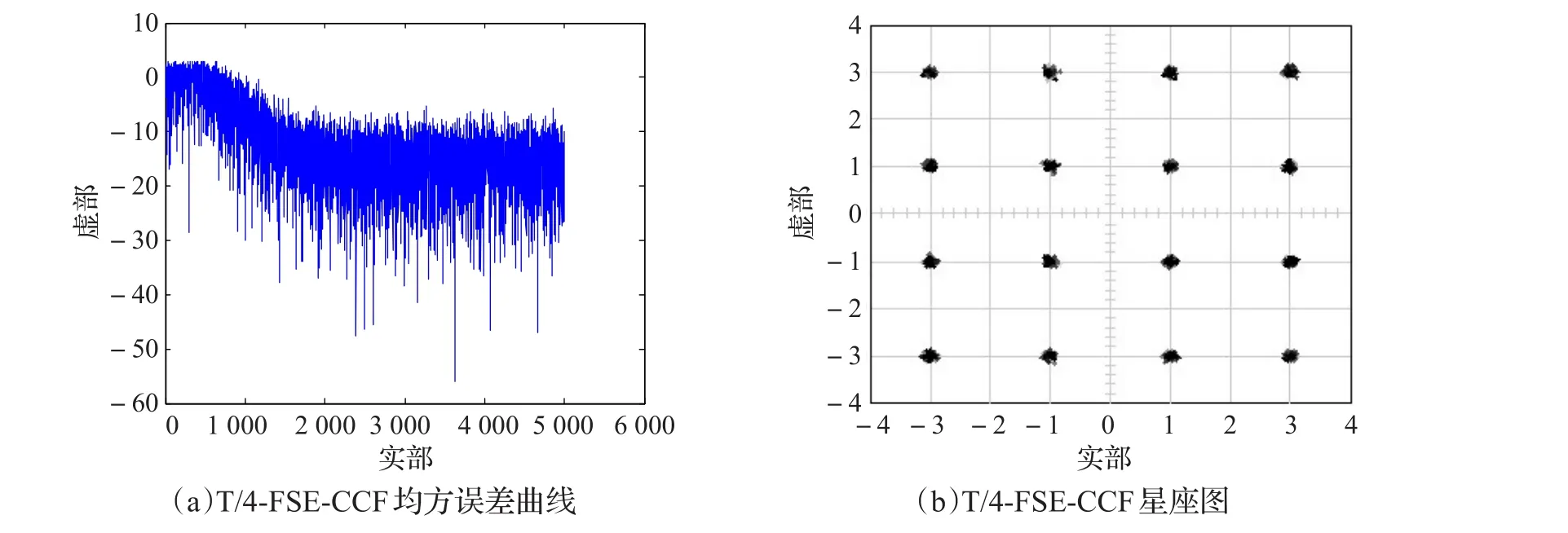
图8 MATLAB的Simulink仿真结果

在对T/4-FSE-CMA算法研究分析的基础上，针对非常模QAM信号，提出了一种基于余弦代价函数T/4分数间隔盲均衡算法（T/4-FSE-CCF），该算法将常模的代价函数用余弦代价函数来替代，与T/4-FSE-CMA相比，T/4-FSE-CCF摆脱了T/4-FSE-CMA对统计模值的依赖，且代价函数能够在信道完全均衡时趋于零，从而加快了收敛速度，减小了稳态均方误差。

为了验证所提T/4-FSE-CCF的有效性，通过MATLAB的M文件对T/4-FSE-CCF的性能进行验证，在获得算法最佳性能的参数值后，进一步搭建了T/4-FSECCF的Simulink模型，并进行了仿真，结果验证了算法的有效性。