基于最大团的层次化重叠社区发现算法
孙成成,席景科,占文威,李 懂
中国矿业大学 计算机科学与技术学院,江苏 徐州 221116
1 引言
早期很多传统的社区发现算法在挖掘社区结构时都是基于网络中节点的唯一性的,即每个节点都从属于某一个社区。然而,近些年研究发现,大量真实网络的社区结构并非如此泾渭分明,很多社区在某些方面彼此具有较为紧密的联系,社区之间存在交叉重叠现象,因此,社区结构通常具有重叠性和层次性。
现有的能够检测重叠结构的社区发现算法主要包括基于派系过滤的算法[1]、基于连边划分的算法[2]和基于局部挖掘的算法[3],这三类算法分别以团(最大完全子图)、边以及节点为研究对象来挖掘社区结构。以边为研究对象难以挖掘网络的层次结构,因此不予考虑。以节点为对象不断向外扩展最后形成层次树图是层次聚类算法中最为常见的做法[4-6],这种做法最大的弊端是稳定性问题,主要体现在初始节点的选择上,少数情况下,初始节点不同会导致算法最终结果不同,大多数情况下算法的结果不依赖于初始节点,但算法的复杂度会随其变化,另外,在具有重叠结构的网络中,若一开始就选择了重叠节点,那么对最终结果的影响就比较大了。因此,可以结合派系过滤算法的思想,将最大团(也称为派系、极大团、最大团等,本文统称为最大团)作为扩展对象,由于最大团本身内部结构非常紧密(任意两个节点间均有边相连),因此由最大团组成的社区也具有较高的内聚性,社区结构的质量有一定程度的保证。另外,每个最大团虽然各不相同,但同一个节点却可以出现在多个最大团中,这样就能检测出网络中的重叠节点。基于以上分析,本文提出一种基于最大团的层次化重叠社区发现算法(Hierarchical Overlapping Community Detection Algorithm Based on Maximum Clique),简称HOMA算法,该算法首先找出网络中的最大团,然后对最大团进行扩展,不断合并最大团直到网络中只剩下一个社区,这个过程形成了一个层次树图,通过选择合适的方法对该树状图进行剪枝,就能得到社区划分结果。
2 基于最大团的层次化重叠社区发现算法
2.1 最大团问题求解
最大团问题(Maximum Clique Problem,MCP)是图论中一个传统的组合优化问题,同时也是一个NP完全问题[7],不过由于求解最大团问题算法的不断改进再加上真实网络的稀疏性,这种NP完全问题基本得以解决。经典的最大团挖掘算法如Bron_Kerbosch算法[8],首先选择一个初始节点作为扩展节点,并将其加入集合R,再从旧的P和X集合中删掉与该扩展节点相连的节点,这样就产生了新的P和X集合,旧的P和X集合依旧保留,接下来对新集合中的节点递归执行上述操作,算法返回后将扩展节点从旧的P集合中移除,并加入X集合。Bron_Kerbosch算法效率不高,因为递归搜索了所有情况,其中有些不是最大团的也进行了搜索,后续出现了很多对于该算法的改进[9-10]。文献[9]针对此问题提出了关键点选取策略,通过缩小扩展节点的范围来提高效率。因此,在本文中采用改进的Bron_Kerbosch算法来挖掘网络中的最大团,不过在细微处作些调整,首先是过滤掉节点数较少的最大团,通过设置一个参数k来控制最大团的最少节点个数。一般而言,一个最大团包含的节点个数应不少于3个,这是因为节点数较少的最大团容易成为冗余的团,这种团的每个节点都来源于其他最大团,将这种团考虑在内就意味着进行了多余的扩展操作。此外,算法挖掘到的最大团很可能没有涵盖网络中所有的节点,对于这些节点不能排除在外,可以将其视为节点数为1的特殊的团。
2.2 社区的扩展合并
HOMA算法的第二部分就是对最大团或单个节点构成的社区进行合并扩展形成层次树图,这一部分是整个算法最关键的地方,如何迭代合并社区直接关系到算法的最终结果,首先介绍几个与扩展过程相关的定义。
定义1(重叠节点集合)两个社区间相同节点构成的重叠节点集合可表示为:

其中,Ci表示社区i,V(Ci)表示社区i所包含的节点集合。
定义2(共同邻居节点集合)两个社区间的共同邻居节点集合可表示为:

其中,N(Ci)表示与社区i内部节点相连但不属于该社区的节点集合。
定义3(社区间桥接边)两个社区间的桥接边是指两个端点分别在不同社区内所构成的边,可表示为:

在2.1节通过调用改进的Bron_Kerbosch算法得到最大团集并初始化为社区后,现在要将其进行合并扩展。首先,要解决稳定性问题,即不能随机选择一个社区为扩展起点,而应该根据某种标准进行选择,这种标准也可称为合并两个社区的原则,在合并两个节点时可以依据节点相似度,那么这里可以依据社区相似度,只是节点相似度已经有很多经典算法对其进行研究,而社区相似度则并无一个较为权威的定义,也没有固定的计算公式,为了便于区分节点相似度,本文将社区间的相似度称为社区的耦合强度。
社区的耦合强度反映了两个社区间的关联程度,关于节点相似度已有很多算法进行研究[11-12],社区间的关联程度并没有一个权威的定义,两个社区间联系越紧密,则耦合强度越大,而两个社区间的关联程度又取决于重叠节点、共同邻居节点和社区间桥接边等因素,分析如下:
(1)重叠节点,两个社区间的重叠节点越多,其耦合强度越大,当小于临界值时,这两个社区即为同一个社区。此外,如果一个社区包含相对较少的节点,而另一个社区拥有更多的节点,那么可认为节点少的社区是另一个社区的子社区,则可将两个社区进行合并。
(2)共同邻居节点,共同邻居是影响节点相似度大小的因素之一,而社区是由节点组成的,那么共同邻居也是社区耦合强度的影响因素之一,共同邻居越多,则社区耦合强度越大。
(3)社区间桥接边,社区间的桥接边反映了社区间连接的紧密程度,因此,两个社区间的桥接边越多,那么社区的耦合强度越大。
基于以上分析,综合考虑两个社区间的重叠节点、共同邻居节点和桥接边这三种因素,定义社区耦合强度如下所示:
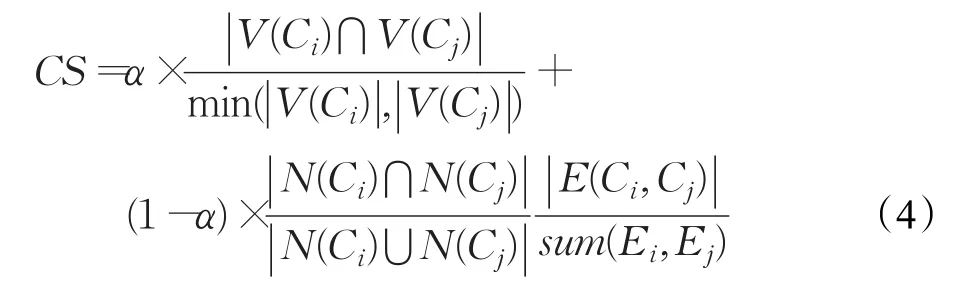
其中,CS是耦合强度,α是调节系数,其值在0至1之间,V(Ci)是社区i的节点集合,则表示社区i和 j共同拥有的节点即重叠节点占其中较小社区的节点个数的比例。N(Ci)表示社区i的邻居节点集合,表示社区i和 j社区的共同邻居节点个数占所有邻居节点个数的比例。E(Ci,Cj)表示社区i和 j之间的桥接边的集合,sum(Ei,Ej)表示社区i和社区 j的边数和。
α是介于0和1之间的调节参数,作用是为了应对不同的情况,社区中除了存在最大团还有许多单个节点。当计算单个节点社区与其他社区的耦合强度时,只需考虑该节点与其他社区之间连边的数量,那么这时候通过设置α的值可以只计算桥接边的比例或共同邻居比例。
定义了社区耦合强度后,需要计算所有社区间的耦合强度,构造耦合强度邻接矩阵,然后从中选择最大值对应的两个社区进行合并,生成一个新的社区,再将两个旧社区从社区集合中删除并计算新社区与其他社区间的耦合强度,之后更新耦合强度矩阵,然后再次选择最大值对应的两个社区进行合并,重复上述操作,由于每次总能找到耦合强度的最大值,因此合并操作能够一直继续下去直到网络中只剩下一个社区为止。在这个过程中,通过记录每次合并社区的序号可构造一个层次结构树状图,树状图的每一层都代表算法得到的一种结果,选择哪一层作为算法结果取决于采用的社区结构质量评价函数,这里将其称为剪枝函数。模块度最大化问题是一个经典的最优化问题,其最大值对应的社区划分即为近似的最优社区划分,本文中依然采用模块度函数,由于涉及到重叠结构,因此采用文献[13]提出的适用于重叠社区结构的模块度函数,其定义如下:

其中,Ov表示节点v所从属的社区个数;Avw表示节点v和w间是否有边相连,值为1说明有边相连,反之则无;kv表示节点i的度;Ci表示i所属的社区;m为网络中的总边数。模块度表示社区划分的精确程度,基于模块度最优思想,模块度值越接近1,划分的社区结构越好。当模块度值达到最大时,说明此时的社区划分结构近似最佳[13-15]。需要注意的是,尽管是最后进行剪枝操作,但模块度的计算不应放在最后,而是在每次合并社区导致社区结构发生变化时更新模块度,这样在生成层次树图的同时,每一层对应的模块度也都计算完毕,这时只需要选择模块度最大的一层作为算法的最终结果,算法终止。
2.3 基于最大团的层次化重叠社区发现算法
HOMA算法能够同时检测网络中的层次结构和重叠结构,其主要包括提取最大团、扩展社区生成树状图以及对树状图进行剪枝这三个步骤:
(1)采用改进的Bron_Kerbosch算法提取网络中所有的最大团,由于节点个数小于3的最大团较多且容易成为附属最大团(团中的节点都来源于其他团),因此可设置一个参数k来控制最大团的最少节点个数,即提高了正确度同时降低了计算量。然后将所有的最大团以及未出现在任何团中的单个节点初始化为独立的社区。
(2)计算网络中任意两个社区间的耦合强度,构造耦合强度矩阵,然后矩阵中最大值对应的两个社区进行合并,得到新的社区,再计算新社区和其他社区间的耦合强度,更新耦合强度矩阵。这样每次总是合并矩阵中耦合强度最大的两个社区,然后更新矩阵,直到最后只剩下一个社区,在这个过程中就生成了一个层次树图。
(3)利用重叠模块度函数对树状图进行剪枝,选择模块度最大的一层作为社区划分结果。
3 实验分析与结果
通过展示HOMA算法在不同网络上的实验结果来验证HOMA算法发现层次结构和重叠结构社区的准确度,实验网络包括真实网络和LFR人工基准网络。实验中采用NMI(Normalised Mutual Information)[16]作为社区结构质量优劣的参考标准。NMI的值介于0和1之间,值越大说明两个社区划分的结果越相似,值为1时则两个社区划分结果完全相同。实验环境为:四核1.4 GHz处理器;内存4 GB;操作系统为Windows 7;使用MATLAB及Java编程。
3.1 空手道俱乐部网络
空手道俱乐部网络又称Zachary’s Karate网络,该网络是从现实世界的一个空手道俱乐部抽象化得到的。该俱乐部由34个成员组成,将成员之间的联系抽象为边,则一共有78条边。
HOMA算法的第一步是提取网络中的最大团,将k值设置为3,即只提取节点数不少于3的最大团,这一阶段一共生成了25个最大团,然后将没有被最大团集合涵盖在内的两个节点即10号节点和12号节点初始化为社区,则一共有27个社区,所有社区节点的分布情况如表1所示。

表1 HOMA算法在Zachary’s Karate网络提取的最大团集合
算法的第二阶段是利用公式(4)计算这27个社区间的社区耦合强度,构造耦合强度矩阵,然后选择最大值对应的两个社区进行合并,接下来更新耦合强度矩阵并重复上述步骤直到最终只剩下一个社区,这个过程生成了层次树图,如图1所示。

图1 HOMA算法在空手道俱乐部网络上生成的层次树状图
由图1可以看出,初始的27个社区一共进行了26次合并操作,在最后一次的合并操作后,整个网络中只剩下一个社区,这个社区包含了最开始的27个社区。在每次合并后,更新一次整个网络的重叠模块度EQ,结果如图2所示。图2中,在第25次合并时,模块度值达到最大值,即此时社区结构划分最为理想,因此将这一层作为该网络的近似最优划分结果。此时划分,则一共得到2个社区,这与Zachary’s Karate网络原本的社区数量吻合。进一步分析发现,节点3和9均出现在两个社区内,因此这两个节点为重叠节点。
为了能够更直观地分析HOMA算法发现的社区结构的质量,将其与LFM算法以及CPM算法在Zachary’s Karate网络上的实验结果进行比较,结果如表2所示。CPM算法用K-clique(大小为K的完全子图)来表示社区,通过某种策略来合并相邻K-clique,那些属于多个K-clique的节点即为重叠节点[1,17]。Lancichinetti等人于2008年提出了可以同时检测网络重叠结构和层次结构的LFM算法,算法是一个将随机种子节点进行迭代扩展形成社区的过程,扩展策略是优化适应度函数,即适应度函数达到局部最大值时才进行扩展[18]。
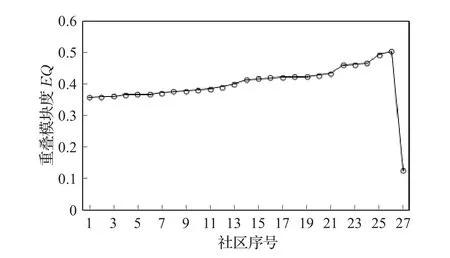
图2 空手道俱乐部网络层次树图对应的重叠模块度值

表2 HOMA、LFM以及CPM算法在空手道俱乐部网络上的结果
从表2可以看出,LFM算法与HOMA算法均得到了2个社区,而CPM算法则为3个,并且发现的重叠节点即1号节点是原本网络中的两个核心节点之一,不应该被归为重叠节点,因此,CPM算法在Zachary’s Karate网络上的结果不太理想。进一步分析发现,LFM算法和HOMA算法得到的两个社区与原本社区均出入不大,但LFM算法发现了5个重叠节点,因此,NMI值和EQ值比HOMA算法低,但结果也较为理想。综上所述,HOMA算法在3个算法中实验结果最好,能够发现重叠节点,挖掘到的社区结构质量较好,在Zachary’s Karate网络上的实验效果较为理想。
3.2 LFR重叠网络
第二个实验采用LFR人工网络来验证HOMA算法检测重叠节点的准确率,LFR人工网络的具体设定参数如表3所示。

表3 LFR重叠网络设定参数
按照表3设定参数生成的LFR网络共有5个社区和12个重叠节点,其社区划分及重叠节点如表4所示。
将该网络应用于HOMA算法,结果如表5所示。由表5中数据可以看出,HOMA算法在LFR网络中挖掘出5个社区,与实际网络社区个数一致,发现重叠节点15个,比实际网络多了3个,这种情况属于正常现象,因为网络中存在一些社区隶属度不高的节点,这些节点处于两个或以上社区的中间层,当不考虑重叠情况时,那么这些节点就会被划分到其中某一个社区,而HOMA算法是对最大团进行扩展的,那么这些节点就可能存在于不同的最大团,最终被若干社区同时包含在内,这也是为什么真实网络如空手道俱乐部网络和海豚社会网络均能发现重叠节点的原因。在这15个节点中,共有10个节点与原本网络相同,其正确率约为83.3%,因此,HOMA算法在该LFR网络发现的重叠节点正确率较高。

表4 LFR重叠网络社区分布

表5 HOMA算法在LFR网络上检测的社区分布
为进一步探究不同模糊程度的社区结构对重叠节点正确率的影响,通过改变γ的值,进行多个网络的实验,得到如图3所示的曲线图。从图3可以看出,当γ≤0.2时,由于社区结构较为明显,则HOMA算法识别正确重叠节点的比例较高;当0.2<γ≤0.4时,此时HOMA算法随着γ的增大其识别重叠节点的比例开始下降,但依然能够发现大部分正确的重叠节点;当γ>0.4时,由于社区结构逐渐模糊,重叠节点正确率下降较快,此时还能够发现一小部分正确的重叠节点,而当γ超过0.6时,社区结构变得很不明显,此时重叠节点正确率很低,说明HOMA算法在这种结构的社区效果不理想。

图3 不同γ值下的重叠节点正确率
4 总结
本文提出一种最大团的层次化重叠社区发现算法,该算法首先提取网络中的所有最大团,但是网络中存在附属最大团,附属最大团中的所有节点全部来自其他最大团,显然附属最大团会对检测结果产生干扰,为了消除其影响同时降低复杂度,对最大团的节点个数设置k值。其次,将网络中的所有最大团和单个节点当作单独社区,并用自定义的社区耦合强度对社区进行扩展合并,每次合并相似度最大的两个社区,直到网络中只剩下一个社区,这样就形成了一个系统树图,最后用重叠模块度对系统树图进行剪枝,得到重叠社区划分结果。

