Redis压缩列表研究与优化设计
张慧宁,李拥军,王绍东
1.广东石油化工学院 实验教学部,广东 茂名 525000
2.华南理工大学 计算机科学与工程学院,广州 510006
3.腾讯科技有限公司 MIG安全云部,广东 深圳 518000
1 引言
传统关系型数据库建立在关系模型基础上,借助集合代数等数学概念和方法来处理数据库中的数据[1-3]。随着互联网业务与数据量逐渐增大,传统数据库存在单机(单库)性能瓶颈且扩展困难的先天性缺陷,无法满足日益增长的海量数据存储及其超高并发数据读写性能要求,从而衍生出各种不同的NoSQL数据库产品[4-7]。NoSQL简单、易于大规模分布式扩展,并且读写性能优越,常见的有Redis、MemCached以及MongoDB等,其中Redis不仅读写性能高,支持多种数据结构,支持数据持久化,而被广泛使用[4,8]。
Redis作为一个开源Key-Value模型分布式内存数据库,可将用户全部数据分布存储在节点内存空间,极大提升了数据读写操作效率[7]。其包含列表、字符串、集合、哈希、有序集合5种Redis数据结构类型[8-11]。同时每种数据结构类型针对不同应用场景支持不同编码方式,压缩列表(ziplist)为其中之一。
由于压缩列表能节约内存,因此哈希键、列表键和有序集合键初始化的底层实现皆采用压缩列表。压缩列表通过节点的previous_entry_length域(见图1)保存前驱节点长度,便于存储数据时实现查找。但此方法连锁更新时间复杂度为O(N2)。具体分析见2.2节。
本文针对Redis压缩列表连锁更新过程中时间复杂度优化问题,设计了新的内存空间级联扩展操作方式,以降低连锁更新时的时间复杂度,同时优化结构体,提升压缩列表操作性能。
2 Redis压缩列表研究
2.1 压缩列表结构
分析发现,Redis单机服务器每秒读写操作可达6万次,在大多数场景下压缩列表对效率的提升起到了重要的作用[12]。压缩列表(ziplist)是紧凑的数据存储模式,由连续特殊编码的内存字节空间组成,包含多个不同类型节点(entry)的顺序型数据结构[13-14]。其功能是将数据按照既定的编码规则存储在一块内存区域中,该内存在物理上是连续的,逻辑上则被按功效区分为多个部分,其作用是在一定可控制的时间复杂度前提下尽可能地减少不必要的内存开销,从而达到节约内存能耗的效果[15-17]。Redis压缩列表数据结构模型如图1所示。
压缩列表(ziplist)内存布局分header、entries、end三个功能区,其中 header包含 zlbytes、zltail、zllen 属性。entries包含zlentry属性,end包含zlend属性。
zlbytes记录整个ziplist占用的内存字节总数;zltail记录ziplist表尾节点距离起始位置偏移字节数大小(即最后一个节点到压缩列表的起始位置字节数量);zllen记录ziplist包含的节点总数量,但当节点数超过65 535时则需重新遍历整个ziplist才能计算得出节点数量。zlentry保存长度受限的字符数组或整数数组。结尾符zlend用于标记ziplist末端,为特殊值0xFF。
Zlentry将空间划分previous_entry_length域、encoding域、content域。为阅读方便,将previous_entry_length域缩写为prevlen域。
entry的prevlen域用于记录前驱节点所占内存空间字节数,具有1字节或5字节存储形态。5字节存储实例如图1(b)所示,当整体编码值为0xFE000007E1,其中值的最高位字节以0xFE表示,之后4字节0x000007E1(十进制值2017)是前驱节点的实际长度。encoding域,用于记录content存储内容的编码方式。若encoding域首字节高两位为11则content域存储内容为整数编码,否则以字节数组编码表示。末端content域用于存储实际的数据,因此Content域存放的是(十进制值2018)当前节点的值。
压缩列表中每个entry所包含的所有字节位相关的特殊含义都可以通过解析函数zipEntry()使用结构本体zlentry保存,prevrawlensize域记录prevlen域的大小是1或者5,prevrawlen域记录前驱节点所占内存空间字节数,lensize域记录encoding所占内存空间字节数,len域则记录content的长度,hadersize域表示节点的头部大小,保存prevlen与encoding的长度之和,encoding域保存content存储数据的编码方式,指针p则指向content存储的数据内容。

图1 压缩列表数据结构
综上所述,Redis压缩列表适用于小数据量的高性能操作,专注运算上效率的提升。从压缩列表的设计结构中不难看出其紧凑的存储方式对降低内存占用有着明显优势。
2.2 压缩列表连锁更新问题分析
2.2.1 产生连锁更新的原因
压缩列表以节点形式存储,可以有任意多个节点。entry的prevlen域占用的内存空间大小是根据前驱节点长度决定为1字节或者5字节。若首字节为特殊字符0xFE,则表示prevlen域占据5字节内存空间,之后4字节表示前驱节点所占据的内存空间字节数,否则只使用首字节表示前驱节点所占内存空间大小,即1字节长度。因此当ziplist删除一个entry或者新增一个entry时,后继节点的prevlen域所占内存空间大小可能会随之发生改变[18-19]。这种可灵活扩展的特性是直接引发连锁更新问题的根本原因。
压缩列表的存储数据形式等同于增加节点,而增加节点将出现3种可能:
(1)用于记录new节点长度所需内存空间小于等于后继节点prevlen域的表示长度,即两者相等(同为1字节或5字节)。则不需要对后继节点进行内存空间扩展,直接存储前节点数据即可。
(2)后继节点prevlen域长度为5字节,能满足记录new节点的最大空间存储需求,同上,不扩展程序直接更新。
(3)new节点占用的内存空间较大,后继节点的prevlen域现有空间长度不足以保存,程序必须对ziplist进行内存重新分配,并扩展后继节点的内存空间。此种操作方式可能会引发连锁更新问题。
Redis压缩列表连锁更新过程如图2所示。
2.2.2 连锁更新产生的前提条件及出现频率
在实际应用中可能出现一种特殊情况,即ziplist在某一时刻存在多个连续的、长度介于250字节到253字节之间的节点entry1至entryN,由于这N个节点长度均小于254字节,那么entry1到entryN的prevlen域长度均为1字节,此种情况的构成是引发连锁更新的前提条件,如图3(a)所示。
若此时通过lpush命令(头插法)插入一个长度大于等于254字节的新节点“new”,插入后new节点将成为entry1的前驱节点,而此时entry1的prevlen域长度为1字节,不能保存前驱节点new节点的长度,需要通过内存重新分配操作将entry1的prevlen域扩展为5字节,实现entry的prevlen域更新。如图3(b)所示。

图2 压缩列表连锁更新流程图

图3 连锁更新的产生条件及节点扩展方式
同理,由于entry1之前的长度介于250~253字节之间,当完成prevlen域扩展后entry1占用的内存空间会大于等于254字节,而此时entry2的prevlen域长度为1字节,因此亦需将entry2的prevlen域大小由1字节扩展为5字节,随着这一过程的不断进行,Redis需要不断地对entry3至entryN的prevlen域大小进行空间重新分配和内存移动,直到所有entry都满足压缩列表对每个节点的属性要求,将这种连续的特殊entry所引发的连锁操作称为连锁更新。同样,当Redis进行压缩列表删除操作时也可能会引发连锁更新。
由以上分析可知,连锁更新产生频繁程度取决于实际应用数据大小,本文通过实验表明,实际应用数据大小在250~253字节所占比例越大,则连锁更新产生的几率越大。
2.2.3 原算法时间复杂度分析
ziplist原更新算法的时间复杂度问题要探究到一般情况和最坏情况。
现假设在列表区间需要扩展更新的连续节点数为m(m=■rN■,0 则一共移动 由等差公式得: 在一般情况下,由于插入或删除而引起的连锁更新的节点个数m(m≪N)甚至不产生连锁更新(m=0),此时r→0,可设移动一个节点位置一次的时间代价为T(1),则对于产生m个点连锁更新导致的移动节点的总的时间代价为: 即在一般情况下,ziplist使用的时间复杂度为O(N)。 在最坏情况下,同样设移动一个节点位置一次的时间代价为T(1),则对于产生的m个节点,r→1,连锁更新导致的移动节点的总的时间代价为: 所以在最坏情况下,ziplist使用的时间复杂度为O(N2)。 时间复杂度是衡量算法好坏的重要指标。算法执行时间是与算法中基本操作的执行次数成正比。由此可知,原更新算法可进一步优化。优化方案可以分别从算法更新流程和列表结构两个方面进行考虑,后文将从这两个方面分别对算法进行优化,并对二者的性能做分析。 通过2.2节分析可知,产生连锁更新时间复杂度问题的主要原因是:内存重新分配操作以及内存移动操作两个方面因素造成了不同程度的时间消耗。为优化时间耗损,针对原压缩列表更新过程不足,提出连锁更新优化算法方案,减少基本操作的执行次数,使时间复杂度由O(N2)降为O(N)。 优化后流程如图4所示,有效避免了因扩展节点导致的节点重复移动。 优化后算法步骤为: (1)输入更新前的ziplist的首地址 zl,以及原entry(k)节点的起始地址 p。 (2)从ziplist头部信息获取当前ziplist所占内存空间长度: 图4 压缩列表连锁更新优化流程 (3)计算需要扩充的内存空间长度extra。 (4)计算出内容总共需要扩充的空间extra之后,即可对ziplist进行扩充,从后往前进行节点移动,同时对需要更新prevlen字段的节点进行扩充更新。 (5)更新完成后返回zl,算法结束。 其中第(3)步,计算需要扩充的内存空间长度extra的算法步骤为: 步骤1初始化extra=0。 步骤2判断 p所指是否为ziplist的结尾,即若p=ZIPLIST_ENTRY_END(zl),则ziplist不需要扩充内存返回zl,算法结束;否则,执行步骤3。 步骤3获取 p所指当前节点cur=ZlEntry(p),ZlEntry(p)函数参数为某一节点首地址,功能是获取 p所指的节点。 步骤4计算当前节点在所占内存空间大小:Rawlen=cur.prevlensize+cur.encodingsize+cur.contentsize。 步骤5判断该节点是否为尾节点,即若p[Rawlen]=ZIP_END,则无后续节点需要扩充,跳转到步骤4;否则计算出存储当前节点长度所需要的内存空间长度: 步骤6找到下一个节点: 步骤7判断下一个节点是否需要更新prevlen字段记录: 若next.prevlen=Rawlen,则下一个节点prevlen字段记录的前置节点的长度和当前节点在内存中所占空间长度相等,则下一个节点不再需要更新,跳转到步骤4。 否则,执行步骤8。 步骤8判断下一个节点prevlen字段是否需要扩充: 若next.prevlensize≥Rawlensize,则表示下一个节点prevlen字段足够记录前置节点长度,则只需要将下一个节点prevlen字段记录的前置节点的长度为更改为当前节点的长度即可。跳转到步骤4。 若next.prevlensize 步骤9移动到下一个节点,p=p+Rawlen;跳转到步骤3。 优化后操作是将长度为L的新节点插入到列表位置k,实现将数据对某个节点的前插操作,具体操作是先检查插入或删除的位置k合法性,然后查找表中第k-1个节点,统计后续节点所需扩展空间大小,将其向后移动一次。 优化后节点插入示意图如图5所示,其中(b)是(a)移动的最终结果,其中统计所需节点扩展大小的主要操作为: 假设新节点的长度为L≥254字节,原列表有N个节点,插入位置为k,则前k-1个节点不需要移动位置,第k+i个节点e(K+i)后移字节数为(L+(i+1)×EXPANSION),其中 i=0,1,…,N-k,EXPANSION为扩展字节数。 图5 压缩列表时间复杂度解决方案 假设new节点插入的位置共有n个,节点插入任意位置的概率相等,则new节点插入第k位置的概率Pk为设插入第k位置的总移动次数为Tk。 时间复杂度算法推演步骤如下: 当k=n时,移动最后一个节点1次,Tn=1。 … 当k=1时,全部节点各移动1次,总共移动n次,T1=n。 则推算移动次数T的数学期望: 即平均移动次数: 故优化后的时间复杂度为O(N)。 优化后Redis压缩列表进行连锁更新操作时,对节点内存空间重新分配及内存移动操作仅需进行一次,而不是N次。即先进行顺序遍历统计完成连锁更新所需扩展的内存空间大小,然后进行一次内存空间重新分配操作,最后依次倒序对entry(N)~entry(K)进行内存移动操作并对应更新其prevlen域,从而所有节点仅需移动1次。算法在耗时上优于原算法,程序优化后,连锁更新的时间复杂度量级由O(N2)下降为O(N)。 从算法描述看出,_ziplistCascadeUpdate函数用来处理内存空间级联扩展操作。当一个新增节点需要插入列表时,如果原节点的prevlen不足以保存新节点的长度,那么就需要进行扩展[19]。特别是这种扩展操作又可能导致后继节点需要扩展[20]。如图6所示,假设从e(k+1)到e(k+m)这m个节点需要连锁更新,即均为1字节长度。针对这一函数_ZiplistCascadeUpdate()级联更新函数优化后算法实现的核心步骤为: (1)初始化ziplst需要扩充的内存空间 (2)对i=k+1,k+2,…,k+m (3)对i=n,n-1,…,k+m+1 (4)对 i=k+m,k+m-1,…,k+j,…,k+1 (5)若k+m+1!=ZIPLIST_ENTRY_END(zl) 算法结束。 图6 包含多节点的压缩列表 为了直观分析算法优化前后功能差异,下面首先简单描述原算法的算法步骤。 优化前算法核心步骤描述: (1)对 i=k+1,k+2,…,k+m 对 j=n,n-1,…,i+1 Entrymove(j,j+EXPANSION);//节点 j往后移动EXPANSION个字节。 Enlarge(i);//节点i的起始地址不变,但是prevlen字段也扩充了EXPANSION个字节。 Relength(i);//更新第i个节点的prevlen字段的值为前置节点更新之后的长度。 (2)若k+m+1!=ZIPLIST_ENTRY_END(zl)Relength(k+m+1) 算法结束。 在优化前的算法中,对于k+m+1节点及之后的节点,即i=k+m+1,i=k+m+2,…,n,每一个节点在内存里位移量为: L0(i)=EXPANSION×m 而对于i=k+1,k+2,…k+j,…,k+m,每一个节点在内存里位移量 L0(i)=EXPANSION×(j-1) 而对于e(k)节点及之前的节点都未移动,位移量为零。即,i=1,2,…,k,有: L1(i)=0 在优化后的算法中,对于k+m+1节点及之后连续的节点,即i=k+m+1,i=k+m+2,…,n,每一个节点在内存里位移量为: L1(i)=extra 而对于i=k+1,k+2,…,k+j,…,k+m,每一个节点在内存里位移量为: L1(i)=extra-EXPANSION×(m-j+1) 而对于e(k)节点及之前的节点都未移动,位移量为零。即,i=1,i=2,…,k,有: L1(i)=0 将_ZiplistCascadeUpdate()函数优化前后效果进行对比分析可得: 优化后算法中extra=EXPANSION×m。 则对于ziplist中k+m+1节点及之后的节点,有: 对于ziplist中k+1节点到k+m节点,有: 对于ziplist中k节点及之前的节点都有: 通过对比发现,优化前后的_ZiplistCascadeUpdate()函数使ziplist上每个节点在内存中最终的相对位置和状态完全一致,所以_ZiplistCascadeUpdate()函数优化前后功能等效。 优化结构之后重新编译redis,在服务器的实验环境下,通过模拟实验验证其功能,在后期将对结构优化问题进行深入讨论研究,此处只对算法做简要讨论,提供解决思路。 重新设计的压缩列表连锁更新处理流程,虽能将时间复杂度降为O(N),但仍存在连锁更新问题,其根源在于当前节点的prevlen域长度会根据前驱节点的大小进行动态调整。prevlen域用于实现压缩列表逆序遍历,若将其替换为entry_length域放置在节点末尾来记录当前节点长度,亦可实现逆序遍历。entry_length域编码方式与prevlen域一样,但需逆向解析,即若当前节点长度大于等于254,entry_length域占5字节,末字节为固定值0xFE,标识前4字节表示当前节点长度,此时可使用属性zllen结合entry_length域获取末尾节点位置,故可删除属性zltail。 优化后的压缩列表如图7所示。 图7 优化后的压缩列表结构 图7 (b)中enconding记录整数编码占用1字节,content存放整数内容占用5字节,entry_length域用于存放自身节点在内存空间中的长度,所示节点总长度占用6字节小于254字节,则entry_length用1字节表示即可,记录为0x6。由图7(a)、(b)中对比看出,结构体优化从根本上改变了原结构记录前驱节点长度的特征。 在保证算法正常逆序遍历,且按上文所示对节点进行存储结构调整,优化后的算法功能和原算法功能是等效的。对算法的功能及性能的验证在实验过程中将做详细的对比分析。 结构调整后优化算法逆序遍历的实现步骤: 步骤1输入压缩列表ziplist,其首地址为zl。 步骤2 解析zl前6个字节,获取zl信息,得到zlbytes、zllen。 步骤3找到尾节点tail,tail=zl+zlbytes-2,同时将指针p指向zl尾节点的最后一个字节位置。 步骤4判断链表是否已经遍历完或者链表为空,若遍历完成或者链表为空,算法结束,否则执行步骤5。 步骤5解析当前节点的Entry_Length字段,确定指针 p所指节点的实际空间长度len以及用来表示该长度的变量lensize的值(1字节或5字节)。 步骤6解析节点的encoding字段: 首先执行操作 ptr=p-len+1,此时 ptr指向 p指向的当前节点的encoding字段的首地址。调用解析出编码当前节点所需的内存空间长度encodingsize和当前节点真实内容长度contentlen。 步骤7访问当前节点的实际数据content字段: 以ptr+=encodingsize为起始位置的长度为contentlen的连续内存空间上存放的便是当前节点的实际数据content。 步骤8指针 p往前移动一个节点长度,然后转向步骤4。 为验证新算法性能,抽取可靠数据样本,对连锁更新优化前后Redis服务器对于压缩列表进行插入操作时的处理速度进行统计与对比分析[21]。 实验所需测试环境为服务器1台,配置如下:Intel®Xeon®CPU E5-2620 v2 6核12线程CPU,32 GB内存,240 GB硬盘,操作系统采用Ubuntu16.04LTS版本,数据库为Redis3.0.3版本,脚本环境为Ptyhon3.4.6。 考虑特定情况下执行时间存在一定的随机性,为方便实验结果对比,本实验采用python随机生成10组字符串数据样本,重复实验50次,取其结果的平均值。 实验采用的步骤为:首先通过lpush命令插入单个长度为250~253字节长度的数据样本到Redis数据库,随后通过插入长度为255字节的数据,来触发连锁更新机制,最后统计优化前后两个版本的Redis数据库实例处理每组数据样本所需的时间消耗,缓存占用,性能变化等数据,用来做实验对比。 实验过程中,每插入下一组数据样本前,对Redis数据库进行清空操作,删除上一次数据样本的所有数据,以确保每组数据插入前的初始环境状态完全一致。 压缩列表连锁更新测试方案设计如图8所示。 4.3.1 连锁更新时间消耗对比 针对连锁更新的时间消耗对比问题,实验过程中每次从10 000个数据量开始,每次叠加10 000个数据量,最高为100 000个数据量,重复50次后,取其平均值进行对比验证。 图8 压缩列表连锁更新测试方案 相同数据量下的连锁更新优化前后的时间消耗对比如图9所示。 图9 连锁更新时间消耗对比 对比以上数据和曲线图可以看出,优化了压缩列表连锁更新问题的Redis数据库实例在处理相同数据量,相同连锁更新的情况下,时间消耗更少。 另在实验过程中,对每次Redis数据库实例插入数据时所占用内存空间进行采集,多次重复实验后取其平均值,得到表1数据。 表1 连锁更新优化前后缓存消耗对比 对比优化前后的Redis实例内存占用情况,在数据量相同的情况下,优化后的Redis数据库实例,通过对相同数据量情况下的连锁更新消耗时间以及内存占用情况的对比验证,在不影响Redis原有功能的前提下,表明优化后的连锁更新耗时更少,处理相等数据量的缓存消耗稳定。 4.3.2 优化后Redis服务器插入性能 为了验证连锁更新重新设计实现后,Redis服务器压缩列表增删等操作性能是否有所提升或者下降,使用了ziplist自带的测试工具对压缩列表在列表头部与列表尾部进行push+pop操作,对比连锁更新优化前后压缩列表插入、删除操作的处理速度效率[2]。连锁更新优化前后压缩列表使用头插法(HEAD)与尾插法(TAIL)两种不同操作方式处理相同数据量所需时间分布如图10所示。 图10 头插法与尾插法处理时间消耗对比 实验数据对比分析统计结果发现,连锁更新优化前后压缩列表进行push+pop操作所需的处理时间效率基本一致,并不影响原有的操作处理效率[22]。但不同的操作头插法与尾插法的操作效率差别较大,头插法算法简单但在链表中节点的次序和输入数据的顺序不一致,若希望两者次序一致,可采用尾插法。该方法是将新节点插入到当前链表的尾部上,为此必须加一个位指针r,使其始终指向当前链表的尾部节点。 同时,从压缩列表头插法(HEAD)与尾插法(TAIL)处理时间消耗分布图还可以看出,压缩列表使用头插法进行数据增加、删除操作所需处理时间远大于使用尾插法进行数据增加、删除操作所需处理时间,这是因为头插法(HEAD)操作比尾插法(TAIL)操作增加了一个内存移动过程,数据量越大,所需移动内存字节数越多,因此所需时间更多。 对比优化前后两个Redis服务器实例在处理相同连锁更新情况的数据,优化前的Redis数据库实例随着数据的增加,处理连锁更新所占用时间也随之增加,反之优化后的Redis服务器实例所花费的时间增长缓慢,从实验结果可以看出,优化后的压缩列表在处理连锁更新过程上所消耗的时间大大减少,从侧面反映出当数据量越来越大,优化后的处理连锁更新所用的时间复杂度也从O(N2)减少成O(N),验证了论文中的方案设计思路。 4.3.3结构优化后连锁更新时间消耗对比 为了验证结构体优化后的作用,实验过程中分别采用了3个Redis数据库实例进行对比验证,分别为: 实例1没有采用任何优化的原始压缩列表。 实例2采用优化连锁更新算法后的压缩列表。 实例3采用优化结构体的压缩列表。 对这3个Redis实例进行数据插入,通过与4.3.1小节相同的实验方式对结构体优化后压缩列表进行的测试。分别采集不同数据量情况下压缩列表进行连锁更新所消耗的时间,得到的数据如表2所示。 表2 结构体优化前后连锁更新时间消耗对比 连锁更新时间消耗对比曲线图如图11所示。 图11 结构体优化前后连锁更新时间消耗对比 从上述数据可以看出,采用了结构体优化压缩列表的Redis实例,和采用了连锁更新算法优化压缩列表的Redis实例,在处理相同数据量的情况下,所消耗的时间几乎一致,相比较优化的原始压缩列表Redis实例消耗的时间少,同时表明,结构体优化后的压缩列表与优化了连锁更新算法的压缩列表在处理连锁更新方面时间复杂度几乎一致。 4.3.4 结构体优化后性能验证 (1)固定数据插入对比验证 针对结构体优化前后,数据插入耗时的对比,实验采用两个不同的压缩列表实例,一个优化了结构体,另一个维持原状态,通过对这两个压缩列表分别插入1万~5万个节点数据(单节点长度固定为250个字节),采集每次插入所消耗的时间,多次重复后取其平均值,对比优化前后的时间消耗,得到优化前后时间消耗对比曲线图,如图12所示。 通过以上数据可以表明,在不造成连锁更新的情况下,结构体优化前后,插入数据所消耗的时间几乎等效,不会对压缩列表的性能造成影响。 图12 结构体优化前后无连锁更新时耗时对比 (2)随机数据插入对比验证 实验采用1万~10万个单个长度在1~500字节的节点,在结构体优化前后的压缩列表采用随机头插、尾插的方式进行插入操作,记录压缩列表消耗的时间,重复多次实验后,取其平均值后,得出的数据如图13所示。 图13 结构体优化前后随机插入时间消耗对比 上述实验数据表明一般情况下,结构体优化后对压缩列表插入的数据量越大时,优化效果越明显。 通过多次对比实验验证了两种优化方案的性能,实验测试效果表明,两种方案在最坏情况下对压缩列表的性能优化明显,通常情况下,插入的数据量越大优化效果越明显。 Redis压缩列表连锁更新机制,最坏情况下时间复杂度为O(N2)。针对此情况,提出两种解决方案,第一种是通过设计新的算法,在原连锁更新机制的基础上,先进行顺序遍历统计完成连锁更新所需扩展的内存空间,然后进行一次内存空间重新分配操作,从而将连锁更新的时间复杂度降为O(N)。第二种给出压缩列表结构体优化方案,在不影响原有功能的基础上消除了存储节点时由于连锁更导致的时间复杂度偏大问题。由实验结果分析可知,结构体优化后的压缩列表读写操作性能获得了明显提升,实现了性能优化。 两种方案都有效减少了原方案在出现大量连锁更新时的时间消耗,但是所提出的优化方案是否适合所有场景,在实际应用场景中是否也有较好的效果,还需要做进一步探讨。在优化连锁更新算法方面,针对字符串的长度有较大限制的场景中,这种优化效果尤为明显,比如在对字符长度有要求且用户量巨大的的微博、Twitter等应用,在后续工作中,会着重对各种实际应用场景进行测试,以验证优化的连锁更新算法在实际应用中的效果。在结构优化方面,后续将对Redis底层知识进行深入研究,将实验扩展到实际应用环境中,此处只对算法做简要讨论,为后期进一步优化提供解决思路。
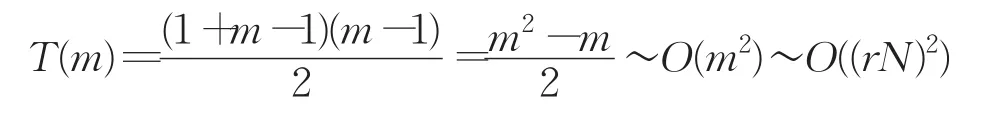
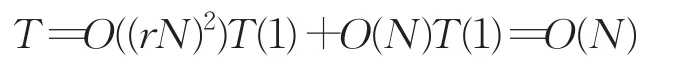

3 优化方案
3.1 连锁更新优化步骤与算法分析








3.2 连锁更新优化算法实现

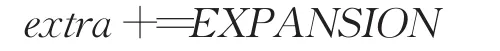




3.3 连锁更新算法优化前后功能对比分析

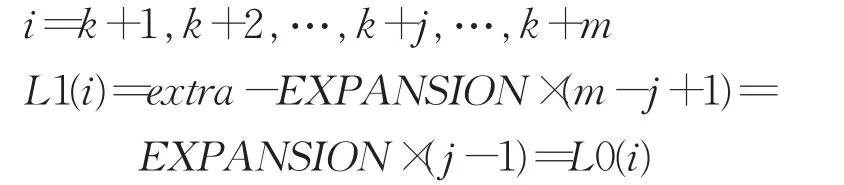

3.4 结构优化

4 实验测试与结果分析
4.1 实验环境
4.2 实验步骤
4.3 实验结果分析








5 总结

