轿车制动器紧急制动瞬态温度场仿真分析
王 兴
(安徽三联学院 机械工程学院,安徽 合肥 230601)
轿车在不同工况条件下制动(高速紧急制动,低速长距离连续制动),制动器温度通常在573.15 K以上。高速制动时,制动器快速升温。制动器温度上升后,摩擦力矩常会有显著下降。还有可能通过钢背将大量的热量传递给制动活塞,导致制动液沸腾或汽化,使制动器完全失效以至于严重影响行车安全。
轿车盘式制动器的制动力要求高而稳定,同时要求振动小,磨损率低。特别是在任何条件下,制动器的摩擦系数都必须保持稳定。唐旭晟建立了三维瞬态温度/应力场有限元模型,利用非线性有限元多物理场方法,较真实地模拟了制动器的制动过程[1]。王国顺从能量传递的角度分析了盘式制动器制动过程能量的转换,摩擦热量的产生机理[2]。李亮基于制动过程中能量耗散的研究,建立循环制动过程中温度场快速分析的有限元仿真模型,应用试验验证仿真结果,确认快速仿真模型的正确性与实用性,从而为制动器的抗热衰退和热疲劳设计提供了系统的解决方案[3]。
轿车紧急制动会将动能转换为热能,属于热力耦合过程,存在大量的非线性因素。随着温度的上升,摩擦力矩会有显著下降,而整车的节能环保也对制动器摩擦副性能提出了更高的要求。因此,深入研究制动摩擦副的温度场状况及分布特点,分析其影响因素,完善其研究方法,对指导制动器的设计、摩擦材料配方的选配,推动摩擦学的发展有很大的参考价值。为了更准确地认识制动器摩擦副温度场分布特点及产热、散热特性,本文基于COMSOL软件,对轿车盘式制动器紧急制动过程中的瞬态温度场展开研究,内容如下:
(1)对实际的制动器尺寸进行一定简化后,建立与实际车型尺寸一致的有限元模型;
(2)建立接触模型,并利用COMSOL多物理场耦合有限元软件求解制动器的三维瞬态温度场分布;
(3)用图表直观地表示出制动器单次紧急制动瞬态温度场的分布状况,分析研究摩擦副接触面温度场对制动器设计的影响,得出一些对后继工作有参考价值的结论。
1 固体传热仿真分析理论基础
1.1 瞬态传热理论基础
一个系统的热参数是随时间变化的温度场称为瞬态传热分析(transient heat transfer analysis)[4]。
瞬态传热与稳态传热的典型区别在于:传热方向上不同位置的热导率在整个瞬态热传导过程中是不同的,并且不同位置之间的物体内热导率随时间的变化呈现不同的差异。
瞬态温度场的基本方程为:

(1)

各单元的导热矩阵Kij,变温矩阵Cij,节点热流量向量Fi分别可以表示为:

(2)
Cij=∭ΩρCNiNjdxdydz
(3)
Fi=∭ΩQNidxdydz-∬S(q-αTf)Nids
(4)
式中:Ω为求解区域;S为给定热流量和对流条件的边界区域;Kx、Ky、Kz分别为材料x、y、z三个方向的导热系数;Ni、Ny为形状函数;α为对流换热系数;ρ为材料的质量密度;C为热容量;Q为物体内部热流量;q为热流密度;Tf为流体的温度。
若采用向后差分法求解瞬态温度场,时刻tn的温度Tn与时间tn+1的温度Tn+1有如下关系:
Tn+1=Tn+Tn+1Δt
(5)
由上述5个方程可以导出瞬态温度场求解公式:
(6)
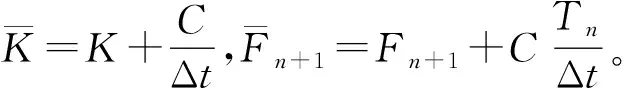
解决传热问题本质上归于求热微分方程解。对瞬态传热问题[5],确定性条件主要有两个:一是初始温度分布的输入时刻状态参数,二是物体的边界上热交换规律[6]。
1.2 有限元分析在瞬态温度场中的应用
瞬态热分析中,热载荷是随时间变化的。对盘式制动器瞬态温度场来说,制动中摩擦副产生热载荷随着刹车盘旋转不断变化,故合适采用瞬态有限元法做相关分析。分析时将整个制动时间划分成若干的微小时间段,假定摩擦副位置固定不动即热源位置不动,在每个微小时间段内输入确定性条件参数(初始状态参数及边界条件等),加载到制动器摩擦副上,采用瞬态温度场求解方程获得瞬态温度解。这里注意的是,上一个微小时间段的瞬态温度解是下一个微小时间段的初始状态参数。不断的循环求解,就可以分析出整个制动过程中摩擦副温度场的变化状况。
2 紧急制动瞬态温度场数值模拟
数值模拟的技术路线:
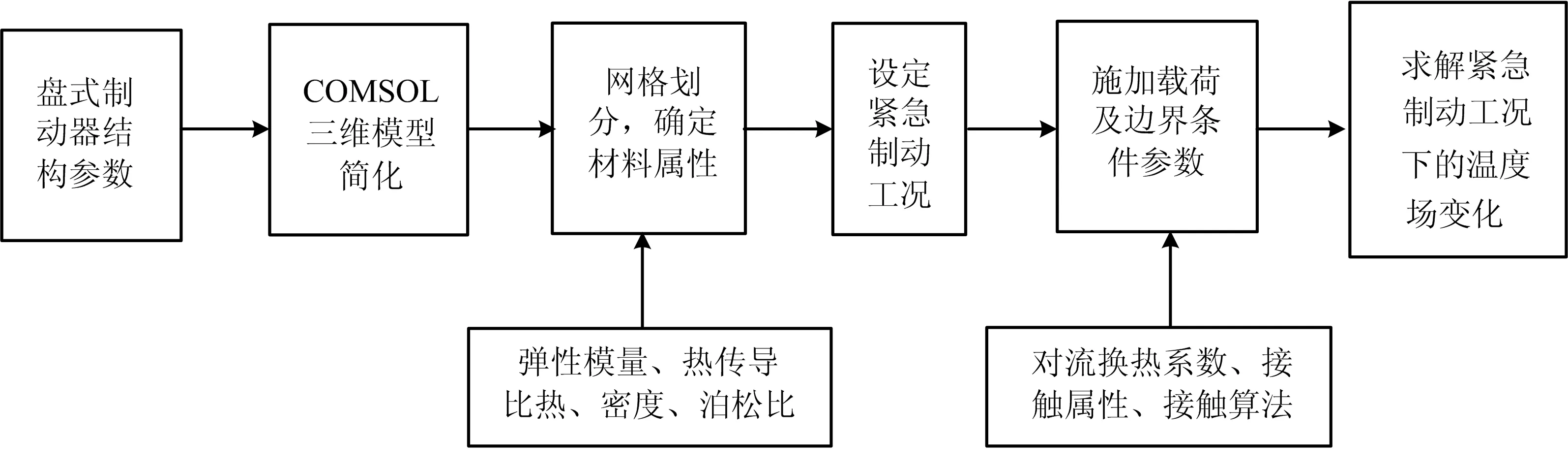
图1 技术路线
2.1 有限元模型的建立
由所研究的盘式制动器组件的实物图(图2)可知,组件中最主要的零件就是刹车盘和刹车片,由它们构成的摩擦副产生大量的摩擦热,同时也耗散大量的摩擦热。因此研究基于这两个零件对单次紧急制动时的瞬态温度场做仿真分析。
根据组件实物,在不影响模拟结果的前提下做出简化模型。图3为简化后的刹车盘及刹车片的三维模型构件。设定:前刹车盘直径280 mm,厚度22 mm,凸台直径100 mm,高度50 mm,同刹车盘底面。构建工作平面为刹车盘上面,刹车片由贝氏多段线构建,前刹车片厚度16.2 mm。
在多物理场耦合有限元分析中,网格的划分比较关键。一般可以根据物理场自由剖分三角形网格。也可以用映射、分布的功能去定义各个模型不同的网格密度。网格划分的越粗,计算的越快,过粗会失真;网格划分的越细,计算速度越慢,但精度较高。本文对于制动器组件的有限元网格划分时,考虑到后续建立摩擦副的需要。将制动盘和摩擦片在轴向上距离接触区域的网格划分的较密,而在远离接触区域划分的较疏。这样即考虑到了计算精度的需要,也控制了计算量,节约了计算时间。网格采用三角形单元,由5 460域单元、5 340边界单元和404边单元组成的完整网格(图3)。

图2 盘式制动器组件

图3 有限元网格
2.2 初始条件与材料参数
本文研究条件:夏季(30 ℃)重量为1 325 kg的汽车正以33.33 m/s的速度行驶,直到驾驶员(75 kg)突然紧急制动3 s。这时,8个刹车片以-7 m/s2的加速度使汽车降速(假定车轮在路上不打滑)。紧急制动3 s后驾驶员释放刹车,汽车以12.33 m/s的速度行驶了8 s,期间未踩刹车。
2.2.1 输入状态参数 对各个输入参数命名赋值(表1)。

表1 输入状态参数
2.2.2 分段函数来定义车速变化 函数定义要求区间起始和结束,以及函数值的物理量为无量纲。以下函数定义使用了单位转换(表2)。整个制动过程的车速变化(图4)。

表2 车速变化函数
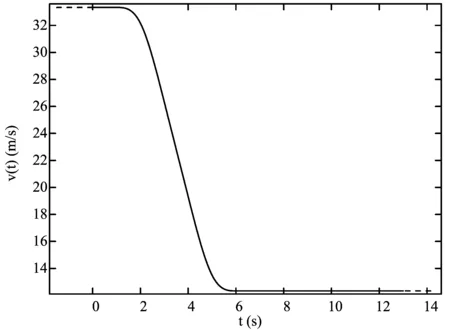
图4 制动过程车速变化
2.2.3 解析函数来定义加速度变化 使用解析函数a=d[v(t),t]定义整个制动过程的加速度变化(图5)。

图5 制动过程加速度变化
2.2.4 定义组件材料属性 刹车盘采用HT250,刹车片采用NAO复合材料。查阅参考文献中的相关资料可知这两种材料的属性参数(表3)[7-9]。

表3 材料属性
2.3 定义组件耦合及边界条件
设定2 s后,刹车盘和刹车片的交界面发生接触。忽略刹车外部的曳力和其他损耗,刹车的延迟功率由汽车动能时间导数的负值给出:
(7)
汽车上8个刹车片中的1个上的摩擦热源为:
(8)
刹车盘与刹车片之间的接触压力与单位面积上的摩擦热源Pb相关,接触压力表达式为:
(9)
这里,摩擦系数μ=0.35,硬化定义:微硬度Hc=800 MPa。
刹车盘和刹车片通过对流和辐射耗散二者边界处产生的热量[10]。本研究将旋转模拟为刹车盘中的对流。局部刹车盘速度矢量为:
(10)
为了仿真贴近实际,保证摩擦副位置固定不动即热源位置不动的前提下,设定组件中的运动约束:刹车片只能做轴向平移运动,刹车盘只能做轴向转动。
2.4 结果与分析
2.4.1 制动过程摩擦副接触面温度场分布特性 选取制动器组件在整个制动过程中的温度变化进行对比分析(假定驾驶员没有应急反应时间),特征时刻选取2 s,5 s,13 s。

表4 制动过程温度变化
由表4可知,整个通风盘式制动器在紧急制动过程中总体的温度变化趋势呈现先增加,后随着制动释放变为下降。
为了进一步分析制动器摩擦副接触面温度变化规律,本文选取摩擦副边缘4个特征点,分别是接触面左端点,接触面右端点,接触面上端点,接触面下端点,分析摩擦副接触面在本次制动过程中的温度变化情况(图6)。由图6可知,4个特征点温度变化趋势一致,均为先急速升温达到极值后下降并逐渐缓慢降温。但随着刹车开始到释放,4个特征点达到温度极值的时间并不相同,并且极值温度也不相同,其中左端点温度极值最高为439.32 K,下端点的温度极值最高为398.45 K,说明摩擦副接触面在本次紧急制动过程中传热温度分布不均匀特性。由于制动过程是热力耦合过程,从而证明制动力在接触面上分布不均匀。
以0.1 s为间隔对接触面温度变化做深入分析,发现开始刹车后的1.3 s(3.3 s时刻),刹车片表面温度达到极值472.24 K,图7可以观察到,最高温度位于刹车片左边缘位置。刹车后的2.2 s(4.2 s时刻),刹车盘表面温度达到极值394.36 K,最高温度位于刹车盘与刹车片接触的左边缘位置。

图6 摩擦副接触面温度变化规律

图7 温度极值时刻
2.4.2 制动过程摩擦副接触面温度梯度变化特性 从表4制动过程温度变化中发现,温度场云图中相同时刻的不同位置温度在空间三轴方向上表现出明显的梯度特征。为了直观的了解制动器摩擦副接触面温度梯度分布情况,依旧选取摩擦副边缘4个特征点,此外再选择1个刹车盘外边缘节点来对比它们在紧急制动过程中3个方向温度梯度的变化情况。5个特征点的等效温度梯度随时间的变化曲线(图8)。

图8 等效温度梯度变化曲线
对比5个特征点的等效温度梯度可以发现,刹车盘外边缘节点的等效温度梯度远小于摩擦副边缘4个特征点的等效温度梯度。此现象发生的主要因素是由特征点位置决定的,当特征点位于摩擦副范围内的热源区域,会受到制动过程摩擦热流的直接影响,升温很快;当特征点位于摩擦副范围之外,仅受到固体传热及环境介质的间接影响而缓慢升温,所以温度上升速度远低于摩擦副范围内的特征点。
2.4.3 制动过程耗散热分析 要计算产生的耗散热量,必须对相应的热耗率变量随时间的变化进行积分[11]。为此,定义两个常微分方程:

(11)
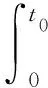
(12)
这两个积分给出刹车盘产热Qprod和散热Qdiss的总热耗率(W)随时间变化的情况。这两个物理量的时间积分Wprod和Wdiss分别提供刹车盘中产生和耗散的总热量(J)。图9显示了摩擦副产生和耗散的总热量与时间的对比图。驾驶员停止刹车后8 s,仅耗散了一部分产生的热量。换言之,为了充分冷却系统,刹车需要保持释放状态的时间远远超过8 s。

图9 摩擦副产热与散热曲线
3 结语
本研究以国产某型轿车前轮采用的盘式制动器为研究对象,应用多物理场有限元软件COMSOL建立热力耦合的有限元模型,在模拟过程中考虑了制动压力、制动盘转速以及对流换热边界条件的实时变化,获得紧急制动时盘式制动器的瞬态温度场分布云图,显示出制动器的瞬时最高温度不是出现在制动结束时,而是出现在制动结束前的某一时刻;分析了制动过程中摩擦副接触面特征点温度变化规律,发现开始刹车后的1.3 s(3.3 s时刻),刹车片表面温度达到极值472.24 K,刹车后的2.2 s(4.2 s时刻),刹车盘表面温度达到极值394.36 K;分析了制动过程中摩擦副接触面温度梯度变化特性,对比5个特征点的等效温度梯度可以发现,摩擦副边缘4个特征点的等效温度梯度远大于刹车盘外边缘节点的等效温度梯度;分析了制动过程中的耗散热,摩擦产生的热量明显大于耗散的热量,且产热速度较快,证明驾驶员停止刹车后8 s,仅耗散了一部分产生的热量。本研究内容可为轿车盘式制动器结构设计与材料选择提供参考。

