一种雷达信号特征参数评估的新方法

， ， ，

(空军预警学院， 湖北武汉 430019)

0 引言

当前，可用于雷达辐射源信号分选识别的脉内特征参数种类繁多、性能各异。近年来，研究者们为了提高信号识别准确率相继提出了时频原子特征、双谱、瞬时派生矩阵、灰度矩、纹理特征[1-5]等10余种新的特征参数。尽管这些特征参数性能稳定、识别率高，但存在着提取算法复杂、应用范围受限等弊端，易造成资源冗余。因此，对特征参数进行科学有效的评估显得尤为重要。

在特征参数评估中，经典方法有基于满意特征选择法、基于粗集理论的特征选择法和基于主成分分析的特征选择法[6-8]。基于满意度特征选择法是针对不存在最优解或难以求出最优解的问题中所提出来的。该方法在“最优”和“满意”中选择“满意”，能将性能指标的满意设计与参数优化融为一体，应用广泛、灵活性强。基于粗集理论的特征选择法则在无需任何先验知识和外部信息的前提下，从大量的数据中挖掘出决策准则，给出属性间的关联关系，但该方法仅能处理离散的属性值，连续性属性需离散化后才能处理。而基于主成分分析的特征选择法则利用映射原理，以信息损失最少为原则将高维数据映射至低维空间中，达到数据降维、简化数据结构的目的。文献[9]基于识别正确率、识别损耗时间、识别方法的复杂性、识别方法的工程可行性，对只有粗糙集理论识别、灰关联理论识别方法及粗糙集理论与灰关联理论相结合的3种识别方法从识别时间、识别正确率、方法优缺点进行了分析。但该评估方法仅基于某一特定指标对信号特征参数进行评估与选择，评估内容单一。基于此，文献[10-11]以特征复杂性、可分离性和稳定性为指标，对特征参数评估。但该方法是以算法语句的频度之和作为时间复杂性，实际应用价值较弱。文献[12]针对上述文献中的不足，对特征提取的算法复杂度和特征稳定度重新定义。文献[13]在上述文献所建立的指标体系基础上，对信号特征参数的可分离性进行了重新定义，但其计算准则仅停留在低维平面中，并未考虑实际应用时分类器核函数对特征参数的影响。此外，文献[14]基于噪声、多径效应、杂波等应用背景提出了一套基于稳定性、置信度、可分性为指标的评估指标体系，并通过建立云决策矩阵和权重云向量对特征的综合效能予以评估。

为此，本文在研究分类器核函数对特征参数影响的基础上，提出了一种新的雷达辐射源信号特征参数评估方法，构建了以可分离性、稳定性和复杂性为评估指标的评估体系，给出了特征类内聚集度与类间聚集度的新的度量准则，并利用层次分析法对不同应用场景下的评估指标赋予权值；其次利用指标评分函数对各指标予以评分；最后通过权重矩阵和指标评分矩阵对各评估对象以综合打分的方式进行评估。将新的评估方法分别应用至雷达辐射源信号实时处理和事后处理两种不同的应用背景中，该评估方法的有效性与可行性得以验证。

1 评估指标的建立与计算

评估指标的建立是进行评估工作的前提与基础，指标选取应遵循目的性、科学性和系统性等原则，但实际评估环境极为复杂，指标易受到多种因素的影响，难以完全满足以上原则。因此，结合雷达辐射源信号脉内特征参数的本质特点从以下3个方面来构建特征参数评估指标体系：

1) 利用特征参数实现雷达辐射源信号的分选识别，关键在于当核函数将特征参数从低维空间映射至高维空间后这些被映射的样本自身的聚集性和不同类样本之间的分离性。因此，选用可分离性来对特征参数的类内聚集度和类间聚集度进行度量。

2) 在实际侦察环境中，信号时频域波形极易受到噪声等因素的影响而产生畸变，从而导致信号脉内特征参数同样会产生变化。因此，选用稳定性来度量噪声对信号脉内特征参数的影响。

3) 在雷达辐射源信号脉内特征参数提取时，特征提取算法的时间复杂度和空间复杂度将直接会影响特征参数的适用范围，而在实际装备中运算平台的运存和内存足够大，空间复杂度可不予考虑。因此，选用复杂性来对特征参数的时间复杂度进行度量。

依据上述指标，构建雷达辐射源信号特征评估体系，如图1所示。

图1 雷达辐射源信号特征评估体系

假设信号特征参数B=[bij]m×n经过核函数K(·，·)从低维空间映射至高维空间后表示为C=[cij]m×m。

定义信号特征的相似性系数为Cr，它表征了两组特征之间的相似性程度，是对特征整体差异度程度的一种度量。特征相似性系数的取值范围是[0,1]，若两组特征完全相关时，该系数取值为1；当两组特征完全正交时，该系数的取值为0。记c1，c2是两组特征，有

(1)

1.1 类内聚集熵

特征参数的类内聚集熵是在特征参数的相似性和信息熵的基础上所提出的，是对特征参数类内聚集度和混乱度的一种度量。当特征类内聚集熵越小时，信号特征的类内聚集度越好，混乱度越小；反之，信号特征的类内聚集度越差，混乱度越大。

记mk为特征参数B经核函数映射到高维空间后映射样本C的均值，其中mk为

(2)

则由信息熵公式可得，信号特征的类内聚集熵为

E=-Crmk,cijlog2Crmk,cij

(3)

式中，Crmk,cij表示mk和cij的相似性系数，由式(1)可得。

1.2 类间聚集熵

类间聚集熵是对特征独立性和混乱度的一种度量，是用来衡量特征间影响程度的指标。当特征类间聚集熵越小，特征间的独立性越差，特征之间的影响程度越严重；反之，类间聚集熵越大，特征独立性越好，特征间的影响程度越小。

记两组特征分别为Cij和Ctk，由式(1)可得到这两组特征的相似性系数。因此，该组特征的类间聚集熵为

E=-Crijlog2Crtk

(4)

1.3 特征灵敏度

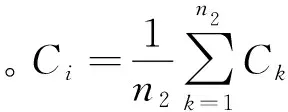
记S1为组内平方和，用来衡量样本内部的随机波动情况：

(5)

特征组间平方和记为S2，用来衡量不同噪声等级条件对特征所引起的差异：

(6)

S1和S2共同组成了特征受噪声的影响程度，因此常用S2与S1两者的比值来进行综合度量：

(7)

式中，F服从自由度为(m-1,m(k-1))的χ2分布，且临界值为Fa，若F>Fa则特征受噪声影响明显，反之影响微弱。

1.4 时间复杂度

目前，针对特征时间复杂度的度量并无标准的方法和依据，其中最直观、最有效的方法为提取该特征时程序所运行时间。因此，本文选用特征提取时程序运行时间作为该特征的时间复杂度。

2 基于用户需求的雷达特征评估模型

Step 1：根据上节中所给出的指标计算规则对指标原始值进行计算，构建评价矩阵C=(aij)m×n,其中m为评价目标数，n为属性指标数。

Step 3：确定指标的评分值。在实际应用中，特征类间聚集熵可用凸递增函数来描述，其评分值随着实际数值的增加而增加，因此其评分函数如式(8)所示；而特征类内聚集熵、灵敏性、复杂度则用凸递减函数来描述，其评分值随着实际数值的增加而降低，因此其评分函数如式(9)所示。

(8)

(9)

式中，bmax和bmin代表指标值b的满意点和无效点。

Step 4：确定评估指标权重W。在雷达辐射源信号识别过程中，可以分为实时处理和事后处理两大类。实时处理时，侦察接收机所截获的雷达信号信噪比低，且实时处理时对样本的稳定性和复杂性有较高的要求；而事后处理时，对稳定性和复杂性则要求不高，识别率才是关键。因此，用户可根据用户经验及实际应用需求，利用层次分析法对各评估指标的权重予以确定。

Step 5：对各评估对象进行综合评分。S=W·Y，W代表各评估指标的权重，Y代表评估对象各指标的评分值。

Step 6：对评估方案进行排序。根据评估方案的总体的评分值，依次对各方案进行排序。

3 应用分析

假定在雷达信号样式和信号脉内特征参数已定的情况下，选用单载频、频率捷变、线性调频、非线性调频、频率编码、二相编码、四相编码、线性调频和二相编码、线性调频和四相编码、相位编码和频率编码十种信号所提取的相像系数、熵值、小波包和复杂度四种信号脉内特征参数，为了使仿真环境贴于实际侦察环境，对这10类信号的载频、脉宽等参数均进行随机产生，并分别在信噪比为-5，0，5，10，15和20 dB下进行实验。在这10种信号的特征参数中，分别取100组特征参数进行训练，取150组数据进行识别 ，并记特征识别率为F1；特征灵敏性为F2；特征时间复杂度为F3。支持向量机(SVM)核函数选取多项式核函数(Poly)。实验结果如表1所示。另有由式(3)和式(4)得到其类内聚集熵及类间聚集熵，分别如表2和表3所示；由式(7)所得的特征灵敏性如表4所示；表5为特征时间复杂度；表6是由式(8)和式(9)所得的评分矩阵。

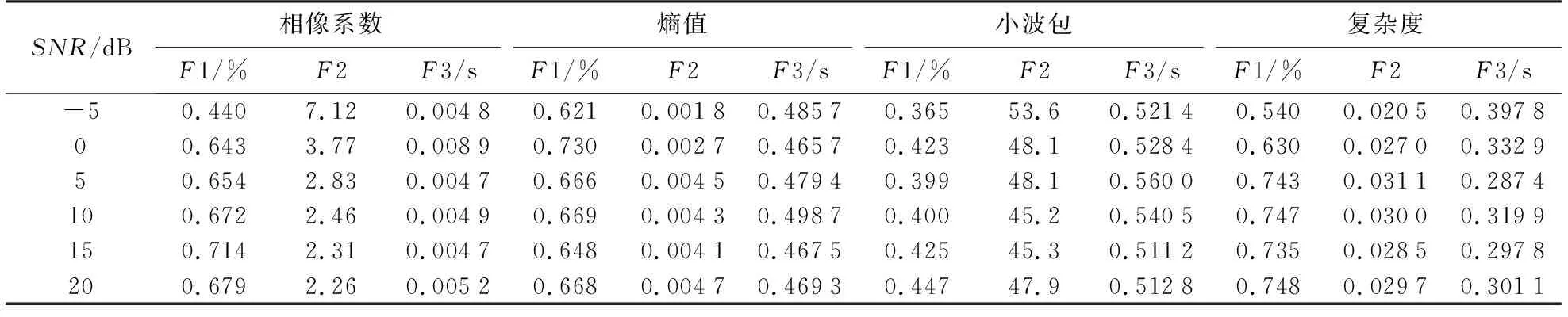
表1 特征参数识别性能

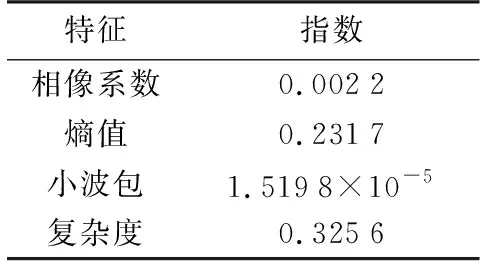
表2 特征类内聚集熵

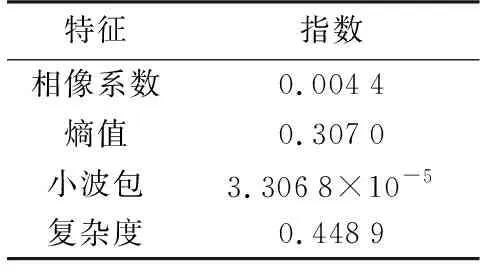
表3 特征类间聚集熵

表4 特征灵敏性

表5 特征时间复杂度

表6 指标评分矩阵

在指标评分中，对于评分值过小的分值近似于0处理。

实验1 基于实时处理的雷达信号特征参数评估

由斯塔相对重要性等级表得信号特征参数实时处理时判断矩阵如表7所示。

表7 实时处理时判断矩阵

此时，该判断矩阵的特征值为λ=3.007 0，一致性指标CI=0.003 5<0.1。因此，此矩阵的一致性可以接受，并由此得到的指标权重为W=(0.079 4,0.079 4,0.403 0，0.438 2)。根据表6的评分矩阵可得各指标的评分值依次为：89.847 1，36.826 4，69.467 3，82.828 5。

由表1特征参数识别结果可知，在信噪比小于10 dB时相像系数的时间复杂度最小，且特征灵敏性较为折中，虽然识别率较低，但满足雷达辐射源信号实时处理时对处理速度要求高，对识别结果要求较低的实际情况。因此，评估结果符合实际情况。

实验2 基于事后处理的雷达信号特征参数评估

同样由斯塔相对重要性等级表得信号特征参数事后处理时判断矩阵如表8所示。

表8 事后处理时判断矩阵

此时，该判断矩阵的特征值为λ=3.012 6，一致性指标CI=0.006 3<0.1。因此，此矩阵的一致性可以接受，并由此得到的指标权重为W=(0.370 5，0.370 5，0.133 6，0.119 4)。根据表6的评分矩阵可得各指标的评分值依次为：52.065 1，61.479 0，56.190 9，73.559 2。

当信噪比大于10 dB时，由表1的特征参数识别结果可知，复杂度特征的识别率在4种特征参数中最高，且特征灵敏性较为稳定。因此，评估结果符合实际情况。

4 结束语

特征参数性能的优劣决定了雷达辐射源信号分选识别效果。因此，本文在研究分类器核函数对信号特征参数影响的基础上，提出了一套完整的特征参数性能评估方法，首先建立了以可分离性、稳定性、复杂性为评估指标的评估体系，并给出特征类内聚集度与类间聚集度的新的度量准则，并基于用户实际应用背景利用层次分析法对各评估指标赋予不同的权重，最后利用综合打分的方式对各评估对象的性能予以评估。将该方法运用至特征参数性能评估的仿真应用中，仿真结果验证了该评估方法的可行性和有效性，具有一定的实际应用参考价值。