基于LDLPP的SAR目标型号识别
, , , ,
(1.陕西师范大学计算机科学学院, 陕西西安 710119;2.中国兵器工业第203研究所, 陕西西安 710065;3.西安电子科技大学雷达信号处理国家重点实验室, 陕西西安 710071)
0 引言
合成孔径雷达(Synthetic Aperture Radar,SAR)几乎不受气候条件的影响,可以全天时、全天候地进行工作[1-3]。致力于从复杂的地物场景中有效地检测到目标,并对检测到的目标进行SAR目标识别,这一技术旨在实现目标的属性、类型或型号的判定[4-6]。同类型不同型号的目标被称之为变形目标[7],目标型号识别比类型识别能够提供更多的目标细节信息。目标型号识别的研究在感兴趣目标细节信息获取、战场感知、精确打击等方面具有重要的意义。
对于目标的类型识别而言,国内外学者已经提出了诸多有效的算法[8-10],而对于目标型号识别的研究方兴未艾[7],目标的型号识别对数据细节特征的准确捕获与保持提出了更高的要求。局部保持投影(Locality Preserving Projection, LPP)[11]是一种基于流形学习的特征提取算法。不同于传统的基于欧氏空间的特征提取算法,如主成分分析(Principle Component Analysis, PCA)[12]、线性判决分析(Linear Discriminant Analysis, LDA)[13]等,局部保持投影在更符合数据实际分布的流形空间中进行特征提取,能更好地捕获数据的本质结构特征。利用局部保持投影算法对数据进行特征提取,能保持特征提取前后数据的局部结构。然而对于实际的SAR图像空间而言,由于目标具有方位角敏感特性[14-15],对于某一个样本而言,在高维空间存在一些和它不同类的样本离其距离很近,希望当样本被投影到低维空间时,它们之间的距离能够被拉远。
针对此问题,本文提出一种融合类别信息的局部保持投影算法以实现SAR目标型号识别,所提算法利用样本的先验类别信息构造能反映样本之间关系的相似性矩阵和差异性矩阵。通过相似性矩阵保持同类样本降维前后的局部结构,通过差异性矩阵扩大降维后异类相似样本之间的距离。采用MSTAR数据进行SAR目标型号识别,验证了所提算法的有效性。
1 融合类别信息的局部保持投影算法
数据的局部结构对于识别而言至关重要,希望降维前后数据的局部结构能够得到保持,即希望在高维空间距离近的数据在映射到低维空间后,相应的数据距离仍然近,也就是说,希望能尽可能地保持数据降维前后的局部结构信息。为此,可建立如下的目标函数:
(1)
式中,yi=ATxi,X={x1,x2,…,xn}∈RD为原始的训练样本集合,Y={y1,y2,…,yn}∈Rd为降维后的训练样本集合,n为样本个数,D和d分别为降维前后数据的特征维数,d≪D,A={a1,a2,…,ad}为D×d维的投影矩阵,S为相似性矩阵,反映了样本之间的相似性,为了保持同一类目标所有样本之间的内在关系,这里将Sij定义如下:
(2)
式中,t1为常数。
由式(2)可知Sij=Sji,即S是一个对称矩阵,当样本xi和xj在高维空间中是近邻点时,S会施加一个大的惩罚,这样最小化目标函数就意味着在高维空间为近邻点的样本在低维投影空间仍会为近邻点。对目标函数作如下代数变换,可得

tr(ATXHXTA-ATXSXTA)=
tr[ATX(H-S)XTA]=
tr(ATXL1XTA)
(3)
式中,H为对角矩阵,对角线元素Hii=∑jSij(或Hii=∑iSij)为相似性矩阵S的行和或列和(S为对称矩阵),L1=H-S为拉普拉斯矩阵。
最小化式(3)得到的投影矩阵A,可保持降维前后同类目标所有样本之间的内在关系。然而,如前所述,仅仅保持数据的局部结构信息并不能实现数据结构全面准确的描述。图像空间中往往还存在着另外一种情况,尤其对于具有目标方位角敏感特性的SAR目标图像而言[14-15]更是如此,即对于某一个样本而言,存在一些不同类的样本在高维空间离其很近,甚至属于彼此的k个近邻点,那么希望当数据被投影到低维空间时,样本之间的距离能够被拉远,以减弱异类相似样本对识别的影响。因为仅仅通过式(2)无法实现异类样本之间关系的描述,为达到此目的,建立如下的目标函数:
(4)
式中,D为差异性矩阵,反映了样本之间的差异性,为了能使在高维空间距离近的不同类样本在投影到低维空间时距离能够变远,差异性函数Dij的表达式构造如下:
(5)
式中,t2为常数,Nk(xi)表示xi的k个近邻点。也就是说,如果xi属于xj的k个近邻点或者xj属于xi的k个近邻点,并且它们属于不同的类别,则在两者之间施加一个如式(5)所示的权值。
由式(5)可知Dij=Dji,也就是说,D同样也是一个对称矩阵,属于不同类的两个样本xi和xj的距离越近,则Dij越小,也就表示xi和xj的差异性越小,可是由于xi和xj属于不同类目标,希望它们投影到低维空间时距离能够变大。最大化式(4)就意味着将xi和xj在低维投影空间里的距离变远。类似地,对目标函数作如下代数变换,可得

tr(ATXGXTA-ATXDXTA)=
tr[ATX(G-D)XTA]=
tr(ATXL2XTA)
(6)
式中,G为对角矩阵,对角线元素Gii=∑jDij(或Gii=∑iDij),为差异性矩阵D的行和或列和(D为对称矩阵),L2=G-D为拉普拉斯矩阵。
因此,在保持同类样本之间局部结构的同时,为了达到异类样本在高维空间距离近的,在低维空间的距离能够变远的目的,可构建如下目标函数:
(7)
将式(3)和式(6)代入式(7),对目标函数进行整理,可得
min||yi-yj||2Sij-||yi-yj||2Dij⟺
mintr(ATXL1XTA)-tr(ATXL2XTA)=
mintr[ATX(L1-L2)XTA]=
mintr(ATXLXTA)
(8)
式中,L=L1-L2。令B=H-G,给目标函数添加约束条件ATXBXTA=I,可得
(9)
利用拉格朗日乘子法求解式(9)所示的含有约束条件的最小值问题,可得
XLXTA=λXBXTA
(10)
投影矩阵A可通过求解式(10)所示广义特征分解得到。A={a1,a2,…,ad}的列向量为式(10)的d个最小非零特征值对应的特征向量,0<λ1≤λ2≤…≤λd。
得到投影矩阵A后,利用投影矩阵将所有训练样本和测试样本投影到低维空间,然后采用最近邻分类器在低维空间进行识别得到识别结果。本文算法的流程图如图1所示。

图1 本文算法的流程图
2 实验结果与分析
为验证所提算法的有效性,本文采用美国DARPA/AFRL提供的MSTAR 数据进行实验[16]。具体的数据描述如表1所示。实验中采用SAR在俯仰角为17°时获得的图像作为训练样本,俯仰角为15°时获得的图像作为测试样本。所有图像的大小均为128像素×128像素,聚束模式下获得的SAR图像的距离分辨率和方位分辨率为0.3 m×0.3 m,图像的方位覆盖范围为0°~360°。图2给出了表1所示10个不同类型目标的光学图像和SAR图像,图3给出了BMP2数据集和T72数据集中不同型号目标的光学图像和对应的SAR图像。从图2和图3可以看出,不同于光学图像,不同类型的目标在SAR图像中表现的十分相似,而同一类型不同型号目标在SAR图像中的差异更小,精确捕获并描述数据的结构信息是实现高精度目标识别的关键。识别时首先从每幅SAR图像的中心截取48像素×48像素的子图像,然后对每幅子图像的幅度进行L2范数归一化处理[17],处理过程如图4所示。选取基于LDA的识别算法[13]、基于PCA的识别算法[12]和基于LPP的识别算法[11]作为对比算法验证所提算法的有效性。识别时,LDA的特征维数为N-1,其中N表示待识别目标的类别个数[13],PCA算法和LPP算法的特征维数为49维,式(5)中的参数k=50,式(2)中的参数t1和式(5)中的参数t2采用5折交叉验证方法在集合{10-2,10-1,100,101,102}中确定。

表1 实验数据描述

图2 10类目标的光学图像和对应的SAR图像

图3 BMP2和T72数据集中不同型号目标的光学图像和对应的SAR图像
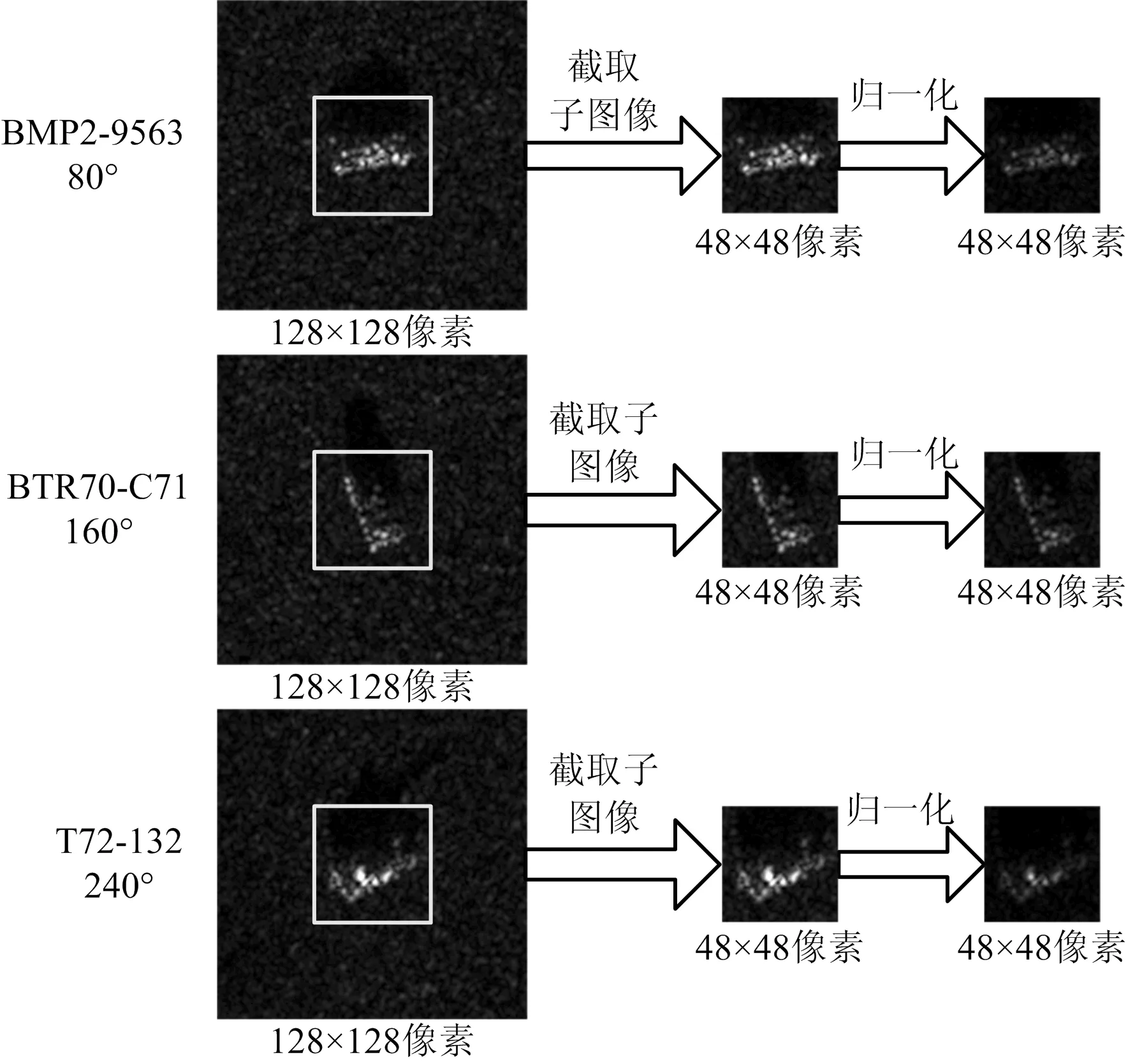
图4 SAR图像预处理示意图
2.1 类型识别
首先进行SAR目标的类型识别,分别进行3类目标识别实验和10类目标识别实验以验证所提方法在数据结构保持方面的优越性。进行类型识别时,目标BMP2和目标T72的训练样本选取BMP2-9563(样本数量为233幅)和T72-132(样本数量为232幅),测试样本则包含目标BMP2的3个型号(样本数量为587幅)和目标T72的3个型号(样本数量为582幅)。首先进行BMP2装甲车、BTR70装甲车和T72主战坦克三个类型目标数据的识别实验。利用训练样本集,构建式(2)和式(5)所示的相似性矩阵和差异性矩阵。采用本文所提算法获得投影矩阵后,对训练样本和测试样本进行降维,对降维后的样本采用最近邻分类器进行识别,相应的识别结果如表2所示。可见,基于LPP算法的识别结果要明显优于基于LDA和基于PCA的识别算法,因为LPP算法成功保持了数据的局部结构。而本文所提算法由于利用了样本的先验类别信息,并且更进一步地描述了数据的空间结构,因此获得的准确识别率要高于基于LPP的识别算法。
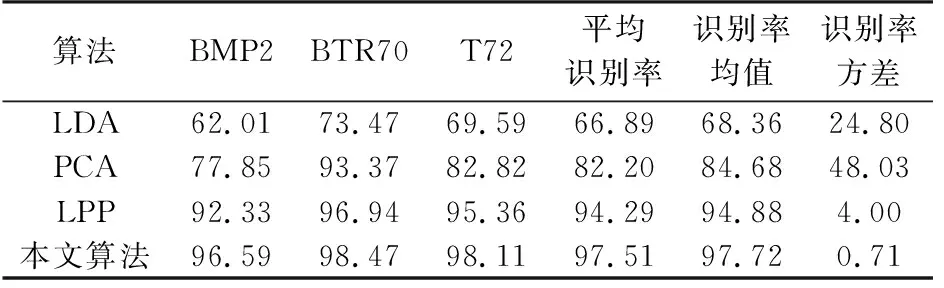
表2 不同算法下3类目标的识别结果 %
为进一步验证所提算法对类型识别的有效性,进行了10个类型的目标识别实验,目标BMP2和目标T72的训练样本选取BMP2-9563和T72-132,测试样本则包含目标BMP2的3个型号和目标T72的3个型号。该实验中,10个类型目标的训练样本总数为2 747,测试样本总数为3 203。实验结果如表3所示。可见,在样本类型增多的条件下,所提算法仍然可以取得91.01%的正确识别率,实验结果验证了所提算法的有效性。
需要说明的是,对于包含多个型号的目标来说,例如BMP2数据集,其包含BMP2-9563,BMP2-9566和BMP2-C21 三种不同的型号。在类型识别中,将其中的一个型号识别为同类的另一个型号,被认为是正确的识别。然而在型号识别中,这样的判决则被认为是误判。可见,型号识别对算法提出了更高的要求。

表3 不同算法下10类目标的识别结果 %
2.2 型号识别
下面进行目标的型号识别以验证所提算法的有效性。首先,将所提算法在BMP2数据集上进行实验,不同算法下的识别结果如表4所示。采用俯仰角在17°录取的全部BMP2数据作为训练样本(样本数量为698),采用俯仰角在15°录取的全部BMP2数据作为测试样本(样本数量为587)。由实验结果可见,采用所提算法进行特征提取可以取得最高的正确识别率,平均识别率比基于LDA的识别算法、基于PCA的识别算法和基于LPP的识别算法的识别率分别高出51.79%,25.72%,12.10%。

表4 BMP2目标型号识别结果 %
接下来采用T72数据集进行实验验证所提算法的有效性,不同算法下的识别结果如表5所示。与BMP2型号识别类似,同样采用俯仰角在17°录取的全部T72数据作为训练样本(样本数量为691),采用俯仰角在15°录取的全部T72数据作为测试样本(样本数量为582)。可见,在所有对比算法中,所提算法的正确识别率仍然是最优的。平均识别率比基于LDA的识别算法、基于PCA的识别算法和基于LPP的识别算法的识别率分别高出40.55%,18.05%,4.99%。
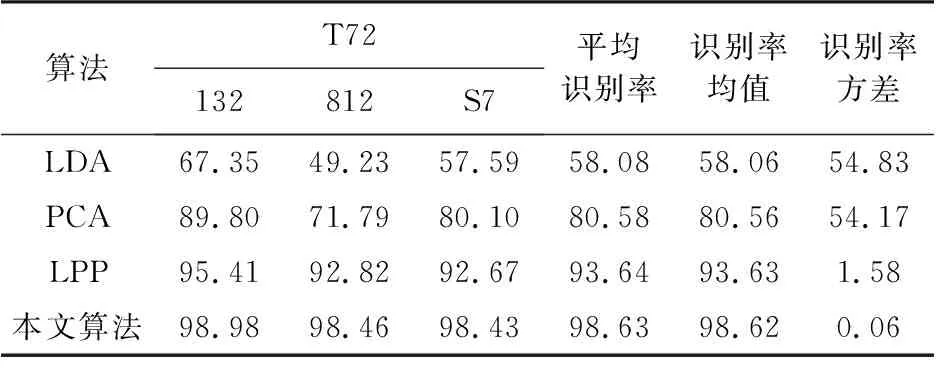
表5 T72目标型号识别结果 %
最后,将所提算法应用于BMP2,BTR70和T72 三类7个型号目标的识别,采用俯仰角为17°时录取的数据作为训练样本(样本数量为1 622),采用俯仰角为15°时录取的数据作为测试样本(样本数量为1 365)。相应的识别结果如表6所示。由实验结果可见,LDA算法由于其原理的限制,识别时的特征维数小于N-1,造成了信息的损失,因此识别率低于基于PCA的识别算法[13]。而LPP算法是基于流形学习的特征提取算法,能够保持数据的局部结构特性,因此比基于欧氏空间的PCA算法和LDA算法具有更好的识别能力。所提算法不仅保持了同类样本的局部结构,而且在特征空间里增大了异类相似样本之间的距离,对识别有利的信息保持得更加完整,因此取得了最好的识别结果。图5给出了不同算法对各个型号目标的识别结果对比,图6给出了不同算法的识别率随特征维数变化曲线,从图中均可看出利用所提算法进行SAR目标型号识别的优越性。

表6 7个型号目标识别结果 %
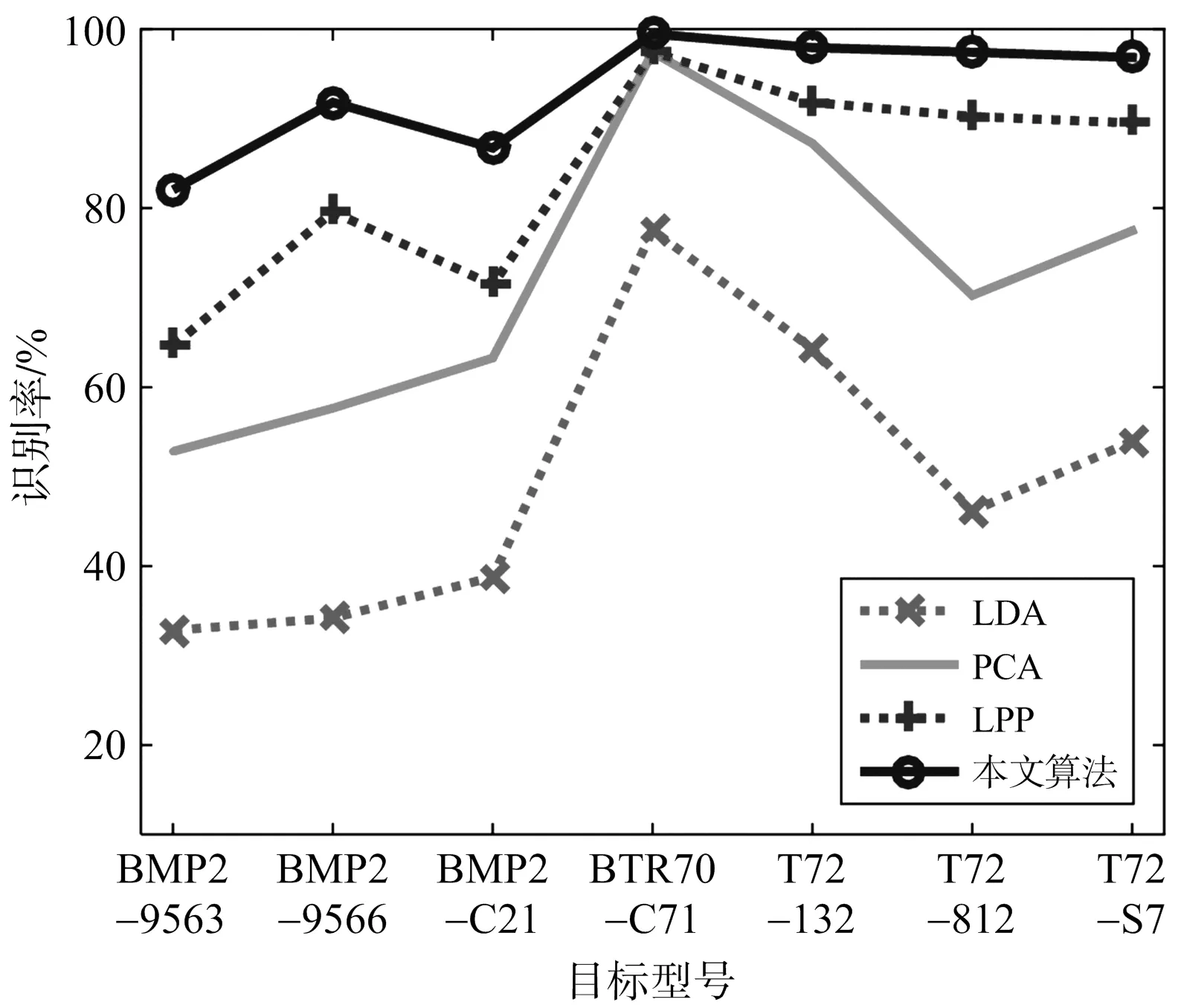
图5 不同算法对各个型号目标的识别结果对比图
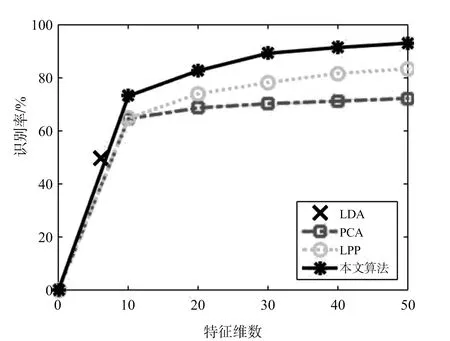
图6 不同算法的识别率随特征维数变化曲线
3 结束语
目标的型号识别可提供更多目标的细节信息,但其较之于类型识别也更加难以实现,对特征提取的要求更高。本文提出了一种融合样本先验类别信息的局部保持投影算法进行SAR图像的特征提取,最终实现SAR目标的型号识别。所提算法在实现同类别目标局部结构保持的同时,还可以有效达到异类相似目标彼此远离的目的。实验结果验证了所提算法进行SAR目标型号识别的有效性。

