MIMO-OTHR稀疏频分互补混沌调制波形设计
, , , , ,
(南昌大学信息工程学院, 江西南昌 330031)
0 引言
超视距雷达(Over-the-Horizon Radar,OTHR)是一种通过电离层对高频电磁波的反射作用探测远距离目标的雷达系统[1]。由于受电离层和海面杂波的影响[2-3],传统OTHR的研究进展比较缓慢。为此,国内外的学者考虑引入新的理论和方法,对OTHR开展新一轮的研究。在2007年的IEEE雷达会议上,来自澳大利亚国防科技组织(DSTO)的Frazer等首次提出将MIMO雷达技术应用到OTHR中[4]。这种通过MIMO分集效应来提高OTHR系统性能和拓展系统功能的新体制超视距雷达称为多输入多输出超视距雷达(MIMO-OTHR)。MIMO-OTHR可以改善传统OTHR在目标检测时面临的距离空间分辨率低、杂波干扰严重、目标探测精度差等问题,对降低目标虚警概率、提升海面低可观测性目标(远距离小舰船和低空飞行目标等)的检测性能具有重要意义。
合适的MIMO-OTHR波形是实现MIMO-OTHR探测的前提和基础。在MIMO-OTHR中,发射波形除了需具备良好的自相关特性和互相关特性之外,还必须兼顾OTHR的应用需求和探测环境。MIMO-OTHR的工作频段,短波电台密集,干扰严重,很难找到连续的、满足信号带宽要求的“寂静”频带。同时,在进行目标探测时,距离单元内的回波极易被海杂波或电离层杂波淹没。同时,在窄频带上集中发射高能量,也容易被敌方截获。因此,本文力求设计一组具有良好正交性能和目标探测性能(距离/速度分辨率、抗干扰性能以及低截获性能等),同时兼顾非连续频率分布频谱环境的MIMO-OTHR正交波形。针对上述背景,本文提出了一种基于稀疏频分正交相位编码(Sparse Frequency Division Orthogonal Phase Coded, SFDOPC)波形设计及优化方法。该波形在每个脉冲中发射多个子带信号,不同子带之间的载频采用稀疏步进频方式,每个子带载频上调制相位编码序列。该波形既保留了相位编码的良好相关特性、抗干扰和低截获特性,又兼顾了可用频谱不连续的情况。同时,与单载频调制波形相比,同时辐射多个载频可以实现展宽信号带宽和获取高分辨率的目的。
对于所提出的SFDOPC波形,最关键的问题是如何设计具有良好性质的编码序列。在雷达领域同时具有理想自相关和理想互相关的编码序列是不存在的。已有的研究主要致力于采用最优化方法获取具备良好自相关和互相关的编码序列。Deng首先将现代优化计算方法引入正交波形设计中,采用模拟退火算法设计了正交多相编码信号[5]。文献[6]提出采用遗传算法设计正交多相码。文献[7]研究应用代数数学方法设计正交多相编码波形。混沌信号由于其本身的随机性,在正交波形设计中具有先天优势,近年来引起广泛关注并得到较多研究。利用混沌具有类随机、无周期、敏感于初始条件等独特性质,使混沌产生的相位编码信号天然具有一定的信号间正交性,以及良好的抗干扰、低截获性能,而利用混沌信号可以产生任意数目,任意长度的编码信号,从而很好地解决SFDOPC波形中调制编码序列数量有限、长度灵活多样性不足的问题。但是,原始混沌序列的相关性能较差,如果直接用于雷达波形探测,将存在高的距离旁瓣和波形相互干扰的问题。为了进一步提升混沌相位编码的相关性能,本文提出了一种混沌互补发射结构来抑制高的自相关距离旁瓣。利用随机产生的混沌序列为初始序列,采用自适应克隆选择算法最优化搜索一对基本互补的混沌序列。同时,SFDOPC波形的多载频频分结构可以进一步弥补有限长混沌序列自身正交性的不足,从而降低波形之间的相互干扰。
1 信号模型及优化设计
1.1 SFDOPC波形模型
1.1.1 波形的数学结构
在MIMO-OTHR中,假设发射阵列是阵元数为Mt的均匀线阵,SFDOPC波形发射信号为S=[s1(t),s2(t),…,sMt(t)]T,其中第m个通道发射的波形信号sm(t)为调制在载频fm上的相位编码信号,其数学表达式为
sm(t)=Am(t)exp(j2πfmt)=
m=1,2,…,Mt
(1)
(2)
(3)

l=0,1,…,L-1
(4)
式中,Am(t)为信号sm(t)的复包络,u(t)为码元调制的矩形脉冲函数,fm为稀疏频分的第m个发射信号的载频,am(l)为相位编码序列,Mc为相位编码的相数。其波形结构为每个发射阵元发射中心频率为f1,f2,…,fMt的载波脉冲信号,每个载波脉冲上调制码元宽度为Ts,编码长度为L的相位编码序列,脉冲宽度为T=Ts·L。根据SFDOPC波形的数学表达式可知,该波形的主要特点在于:一是采用了MIMO雷达中的分频技术,在获取正交性的同时,扩展了信号带宽,提高了频谱利用率。各个发射通道的载频选择不是确定的,而是根据对OTHR频谱进行实时监测后确定的,从而可以有效避开干扰频带。二是在每个发射载频上进行了相位编码调制。
1.1.2 混沌相位编码调制
混沌信号可控,易于产生、存储和恢复。因此,选择混沌序列作为相位编码的基础,可以保证编码信号的随机性、安全性,且编码数量和长度要求可以满足。本文选取离散混沌序列作为产生相位编码的基础,在迭代产生混沌序列后,需要对该序列进行量化编码,得到相应的相位编码序列。假设混沌序列为xm(l),l=1,2,…,L,xm(l)可由一个非线性混沌迭代Φ(·)产生,即
xm(l+1)=Φ(xm(l))
(5)
不失一般性,假定xm(l)∈(0,1)。相位编码序列am(l)是由混沌序列xm(l)量化映射得到,具体的映射步骤如下:
1)为混沌映射选择一个初始值xm(0),且xm(0)∈(0,1)。
2)根据式(5)的混沌迭代,产生序列{xm(n)},1≤n≤L+999。为了降低初始值的影响,去掉前1 000个点,提高混沌序列的复杂度。可得到一个混沌序列{xm(l)},l=0,1,…,L-1。
3)由映射am(l)=2π·ceil(Mcxm(l)-1)/Mc,可得到基于混沌的相位编码序列{am(l)}。
重复以上步骤Mt次,可获得包含Mt个混沌相位编码的序列集{am(l)},m=1,2,…Mt,l=0,1,…,L-1。由于这Mt个序列是独立随机产生的,它们之间是近似相互正交的。将产生的混沌相位编码序列集调制在Mt个载波上,便可得到基于混沌相位编码的SFDOPC波形。
1.1.3 接收信号处理
对于一个雷达接收端,假设Mt个波形回波信号同时到达,当对回波信号进行匹配滤波时,会引入由(Mt-1)个波形的互相关带来的相互干扰。对于Mt个波形,在接收端存在和波形s1(t),s2(t),…,sMt(t)相对应的Mt个匹配滤波器,这些匹配滤波器的总体输出可表示为
(6)
式中,S为发射波形集合,Raa(·)为自相关函数,Rcc(·)为互相关函数。 由式(6)可以看出,接收端的脉冲压缩输出是由波形的自相关和互相关决定的,那么为了降低脉冲压缩的输出旁瓣水平,有必要对波形的自相关和互相关性能进行优化。自相关和互相关函数的表达式如下:
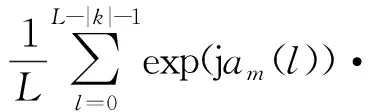
exp(-jam(l+|k|))·
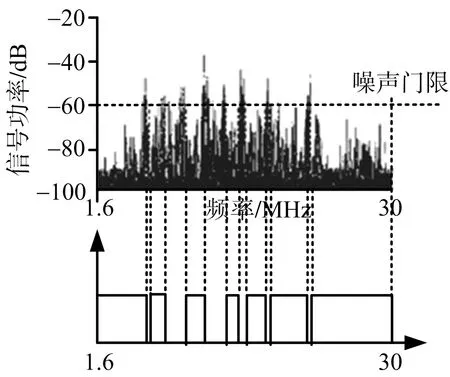
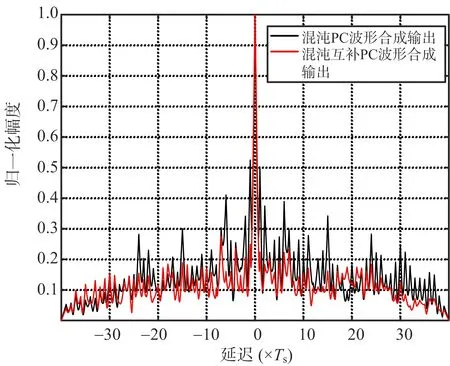
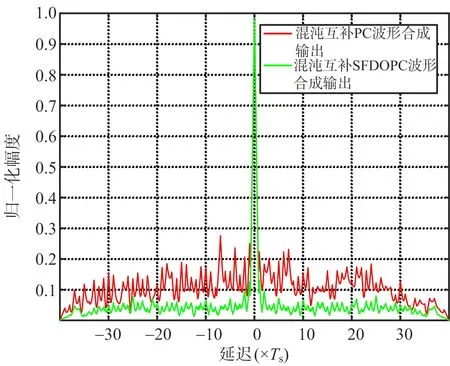
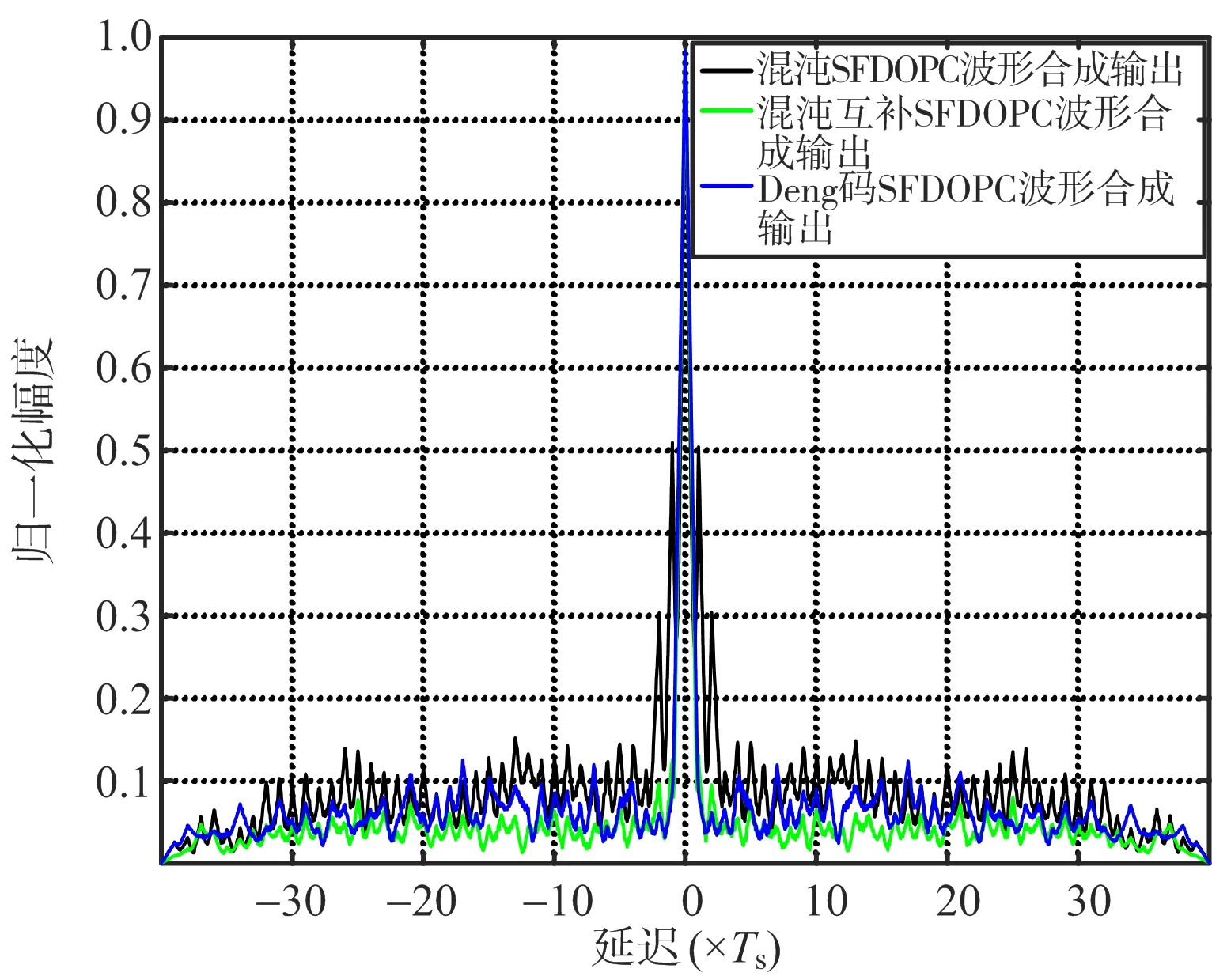
exp(-2πfm|k|),0≤|k| (7) Rcc(sm,sn,k)= m≠n,m,n=1,2,…,Mt (8) 由Raa(·)和Rcc(·)的计算公式可知,匹配滤波器输出Rr(S)的旁瓣水平与相位编码序列自身的相关性有关。为此,本文考虑构造一种混沌互补发射结构来抑制混沌相位编码较高的自相关距离旁瓣,并利用SFDOPC波形的多载频频分结构来降低各发射波形之间的时域互相关。 1.2.1 互补发射结构及波形优化建模 一对位数相同的有限序列,如果其自相关函数之和呈现理想的非周期自相关特性,则称它们为互补序列。已有互补码的码序列长度和序列个数十分有限。为了得到任意长度、任意个数、任意相数的互补相位编码序列,这里基于混沌编码信号,采用最优化搜索的手段,来构造近似互补混沌编码序列以抑制距离旁瓣。假设第m个发射天线发射的第一个基带相位编码信号为Am(t),其对应的第二个脉冲上调制的最优互补相位编码信号为Bm(t),Bm(t)可表示为 (9) l=0,1,…,L-1 (10) 定义Am=[am(1),am(2),…,am(L)]和Bm=[bm(1),bm(2),…,bm(L)]为相应的相位编码调制序列。对于完全理想的互补码,当多普勒频移为零时,Am和Bm将满足以下条件: Raa(Am)+Raa(Bm)= (11) 将混沌互补编码序列调制在发射载波上,则可由Am(t)和Bm(t)结合得到sm(t)的基带信号Cm(t)为 Cm(t)=Am(t)+Bm(t-Tr)= (12) 式中,Tr为脉冲重复时间,Ts为码元宽度。发射信号为Cm(t)时,脉冲压缩滤波器的合成输出可表示为 (13) 式中,对应m=1,2,…,Mt的每个求和项为Mt个匹配滤波器的输出。理想情况下,脉冲压缩滤波器的合成输出应满足: (14) 为实现对总体输出结果的优化,这里首先对每个匹配滤波器的输出结果进行优化。例如,对应波形sn(t)的单个匹配滤波器输出结果为 Rrn(A,B)=|Raa(An)+Raa(Bn)+ (15) 对于理想的互补相位编码序列对An和Bn,有 Rrn(A,B)=|Raa(An)+Raa(Bn)|= (16) 由于编码长度和相位编码数有限,所以几乎得不到理想的互补码,即式(16)的关系不能够完全满足,只能够寻找近似满足式(16)关系的序列对An和Bn。为此,构造如下代价函数: Eun(B)=min{ISLRrn+μPSLRrn} (17) (18) (19) 式中,μ为PSL和ISL的权重系数。 以上的优化求解可以归结为NP问题,传统的算法由于沿着单方向进行搜索求解,常常容易陷入局部最优,不利于此类问题的求解。免疫算法具有较快的收敛速度和高效全局寻优能力[8],在求解NP问题中相比模拟退火算法,遗传算法等具有更好的优势。所以本文选择自适应克隆选择算法进行优化求解。 1.2.2 自适应克隆选择算法优化产生互补码 克隆算法的实质是在抗体进化过程中,在每代候选解的附近,根据亲合度的大小进行克隆,产生一个变异解的群体,从而扩大搜索范围(即增加抗体的多样性),有助于防止进化早熟和搜索陷于局部极值,同时通过克隆选择来加快收敛速度。其中抗原对应于优化问题的目标函数和各种约束条件,抗体对应于优化问题的优化解,抗原和抗体之间的亲和度函数对应于优化问题的解与目标函数的匹配程度。 本文的目的是要获取Am的最优互补码Bm,将1/Eum(B)作为算法的亲和度函数,寻求最大亲和度函数值下的编码,算法描述如下: 1) 初始化种群 产生1×L的混沌相位编码序列aml,然后再产生Np组1×L的混沌相位编码序列bml(i),其中i=1,2,…,Np。以Np组bml(i)为抗体种群。 2) 计算亲和度并排序 定义亲和度函数为H=1/Eun,针对每一个抗体β,计算它们的亲和度,并排序。 3) 克隆操作 根据各个抗体的亲和度值,计算克隆规模qi,进行克隆。 4) 变异操作 根据各个抗体亲和度函数值排名和进化代数来调节抗体的高频变异概率。如果抗体较差,就对其给予较高的变异率;如果个体较优,则依据其迭代状态赋予此个体相应的变异率(迭代次数越接近最大设定代数,抗体变异率就越小)。 5) 克隆选择操作 对变异后的每一行抗体按亲和度大小选择一个最优的抗体,作为新的种群。 6) 更新种群 种群进化代数加1,以克隆选择出来的种群为新一代的种群。 7) 终止条件 如果达到算法终止条件,算法终止。 将种群中最大亲和度对应的抗体保留,即得到一行混沌相位编码序列am最佳的信号相位补码,否则,转步骤2)。 每次优化可以得到一行混沌相位编码序列对应的最优互补相位编码,重复Mt次,即可得到Mt个混沌相位编码互补对。 在上一节中,利用自适应克隆选择算法,对Rrn(A,B)中的自相关进行了优化,但是,并未对Rrn(A,B)中的互相关进行优化。一方面,由于所调制的相位编码序列为混沌相位编码序列,而且每个发射波形都是独立随机产生,波形集中波形自身的互相关性就较小。另一方面,基于SFDOPC的波形结构,不同的载波发射可以进一步降低不同波形之间的互相关。 OTHR工作的电磁环境复杂,很难得到宽的连续的寂静频带,这使得对当前监测区内工作频段的电磁环境进行实时监测十分必要。为评估当前频谱占用情况,假设一个合适的门限η,如果频段内信号功率低于门限η时,就认为这个频段是可用的,评估示意图如图1所示。显然可用的频谱是稀疏的、非连续的。表1为文献[9]中给出的1999年夏季加拿大某次高频地波雷达试验中得到的可用高频信道组合,不难看出,在5.11~5.80 MHz的高频频带内,可用频带是稀疏分布的。在这种情况下,基于SFDOPC波形结构需要对载波频率进行选择。根据表1提供的可用频谱范围,本文构造了适合波形需求的频谱信道,如表2所示。 由表2可知,本文构造了4个信道,每一个通道的带宽均为20 kHz,相邻通道的频率间隔大于带宽,满足了SFDOPC波形的正交性要求。 频率/MHz图1 稀疏频谱分布示意图 信道频率范围/MHz带宽/kHz15.11~5.143025.26~5.271035.29~5.312045.37~5.392055.46~5.482065.51~5.521075.54~5.595085.64~5.662095.72~5.7310105.77~5.8030 表2 本文构造的频谱信道 按照上述的混沌相位编码波形的产生方法,可以构建任意编码长度,任意数量的相位编码信号满足MIMO雷达发射使用。本次仿真采用发射天线数Mt=4、编码长度L=40的四相编码信号(0,π/2,π,3π/2), PSL和ISL的权重系数μ=1,所使用混沌序列为典型的Logistic映射。仿真图中PC表示相位编码(phase coded)。 仿真一:随机产生4个混沌相位编码波形,并一一求出4个波形对应的最优混沌互补相位编码波形,分别用随机产生的4个相位编码波形和其互补发射结构作为发射波形,求出它们的合成输出,得到图2。由图2可知,相比于随机混沌序列相位编码波形,互补发射结构有效地降低了合成输出的旁瓣,其PSL和ISL都得到了很大的降低。该仿真表明,本文对混沌相位编码信号的优化是有效的。 图2 混沌相位编码波形与混沌互补相位编码波形合成输出对比图 仿真二:Deng码是一种利用模拟退火方法优化得到的经典正交序列集[5],其代价函数对序列的自相关和互相关进行了联合优化。而本文的混沌互补序列集采用的优化方法为自适应克隆算法,主要对互补序列的自相关进行优化,而互相关特性由混沌序列自身的独立性决定。为比较两种序列集的输出性能,图3给出了优化的4对混沌互补序列和Deng码的合成输出对比图。由图3可知,虽然本文方法只对自相关特性进行了优化,但是序列集仍然具有较好的正交性,其输出结果和经典的Deng码输出结果基本一致,甚至要优于Deng码。 图3 Deng码相位编码波形与混沌互补相位编码波形合成输出对比图 仿真三:为了进一步加强混沌互补相位编码波形的正交性,采用SFDOPC波形结构对混沌互补编码序列进行载波调制,降低各发射波形之间的互相关。图4给出了两种情况的合成输出,由图4可知,采用SFDOPC对混沌互补相位编码序列进行载波调制,有效地降低了合成输出的旁瓣水平,验证了采用SFDOPC波形结构可获得更优的匹配滤波输出结果。 图4 混沌互补相位编码波形与混沌互补SFDOPC波形的合成输出对比图 仿真四:为了进一步体现本文设计的混沌互补SFDOPC波形的优越性,图5将混沌SFDOPC波形、混沌互补SFDOPC波形和Deng码SFDOPC波形的输出结果进行比较。由图5可知,混沌互补SFDOPC波形合成输出的旁瓣低于Deng码SFDOPC波形合成输出的旁瓣,远远低于混沌SFDOPC波形合成输出的旁瓣。可见,本文设计的混沌互补SFDOPC波形是一种较优的波形。 图5 3种SFDOPC波形合成输出对比图 本文针对MIMO-OTHR,设计了一种稀疏频分互补混沌调制波形。首先,考虑到MIMO-OTHR工作环境恶劣、“寂静”频带非连续的情况,设计了一种稀疏频率波形的结构。在实时频谱监测后,需合理选择发射频点和波形带宽。然后,将混沌相位编码序列调制在选择的稀疏频点上。采用自适应克隆选择算法对混沌相位编码序列的自相关特性进行优化,得到互补混沌相位编码序列。与此同时,稀疏频点发射的方式可以进一步加强波形的正交性。所设计的波形在混沌相位编码序列的选择上具有极大的自由度,而载波频点的选择也具有较优的自适应性。与经典波形相比,本文所设计的稀疏频分互补混沌调制波形有着更低的匹配滤波输出旁瓣,提高了目标的检测性能,从而不失为MIMO-OTHR中一种可行的优良波形。1.2 互补混沌序列优化
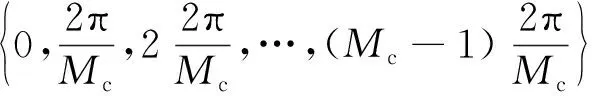
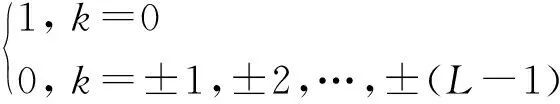
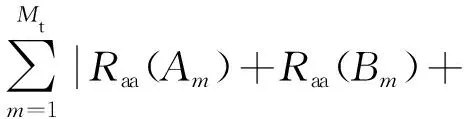


1.3 SFDOPC波形的子带载波频率选择


2 计算机仿真分析

3 结束语

