北斗系统对流层延迟改正模型精度分析

， ， ，

(河南师范大学电子与电气工程学院， 河南新乡 453007)

0 引言

目前世界上有四大卫星导航系统，即美国的GPS、俄罗斯的GLONASS、欧洲的Galileo和中国的北斗系统，其中，北斗卫星导航定位系统是由我国自主研制的区域性卫星导航系统。第一代北斗导航系统(BDS)于2003年开始运行，第二代北斗导航系统(Compass)于2012年底开放运行。目前，北斗卫星导航定位系统运行稳定、工作状态良好，已在渔业、气象、交通运输管理、应急救援等方面获得了很好的应用[1]。

为了提高北斗卫星导航系统的定位精度，应尽力减小各种误差源的影响。根据北斗卫星定位的工作机理，卫星信号需要在大气中传播，这样就会产生大气折射误差，从而影响北斗卫星的定位精度[2-3]。产生大气折射误差的误差源是对流层和电离层大气，它们不仅使得无线电波射线发生弯曲，而且也使得其传播速度减慢(相当于传播路径的增加或者时间上的延迟)，这两种情形都会产生折射误差。相比来讲，在大于3°仰角情况下，电波射线弯曲比传播速度减慢引起的折射误差小得多[4]。因此对卫星导航定位系统，可以忽略电波射线弯曲引起的误差，只考虑因电波传播速度减慢引起的折射误差，也就是大气折射引起的时间延迟。由于对流层与电离层的性质不同，因此常将这两种大气引起的折射误差称为对流层延迟和电离层延迟。

电离层大气为色散介质，可通过对双频测量卫星信号的传播延迟进行差分，从而消除大部分电离层延迟误差，或者采用电离层延迟模型进行改正[5]。对流层为非色散介质，无法利用双频测量方法来消除其延迟误差。另外，目前导航卫星的电离层延迟模型的研究很多，也给出了各种情形下电离层延迟模型的选择建议，而研究北斗系统中的对流层延迟模型较少。尽管相对来讲，北斗卫星中的对流层延迟小于电离层延迟，但是为了提高卫星定位精度，对流层延迟也必须考虑。本文以目前公认的对流层电波射线描迹法为标准，通过与目前常用的3种对流层延迟模型的对比，对各个模型的精度和特点进行分析和总结，可为北斗卫星导航系统提高定位精度时对流层延迟模型的选择奠定基础。

1 高精度的电波射线描迹法

计算卫星信号通过大气层引起的折射误差，目前精度最高的方法是电波射线描迹法，它也是试验靶场检验无线电测量设备精度中的常用方法[4]。该方法一是在假设大气球面分层情况下由电波理论推出计算折射误差公式，其公式本身没有误差，精度只受来源于大气球面分层假设的影响，但这一影响很小。二是该方法采用的折射率剖面由测站的实测探空资料获得，因此其大气参数代表性误差引起的折射误差也很小。这样，该方法的精度比其他相关计算大气折射误差的方法都高，其缺点是不能实现实时计算折射误差。利用电波射线描迹法计算对流层延迟d的公式为

(1)

式中：E为卫星高度角；H，HT分别为用户高程、目标离地高程(m)；h为任意高度(m)；a为地球平均半径，a=6 370 000 m；n为大气折射率；A=(a+H)n(H)cosE；φ为用户与卫星之间的地心张角。

2 对流层延迟计算模型

对流层延迟误差的改正方法主要有高精度的射线描迹法、延迟参数估计法、模型修正法和实测法等，其中，模型修正法在实际应用中较为广泛，且其精度也比较高[3]。针对北斗卫星系统，常采用UNB3,Hopfield和Saastamoinen对流层延迟改正模型[6]。

基于模型修正法的对流层延迟改正模型一般都是将对流层延迟分成天顶延迟和映射函数两部分，这也是目前研究对流层延迟的最广泛、最有效的方法。另外，对流层大气主要由干空气与湿空气组成，其中湿空气在10 km以上已经很稀薄，这样干空气与湿空气引起对流层延迟的变化率就不同，因此采用同样的模型参数就会引起误差。为了减小对流层延迟改正模型误差，常将干、湿空气引起的对流层延迟分开考虑，即对流层延迟由干空气的延迟和湿空气的延迟两部分组成。这样，基于模型修正法的对流层延迟d为

d=ddmd+dwmw

(2)

式中:d为对流层的总延迟量；dd,dw分别为干、湿空气引起的对流层天顶(从地面垂直到对流层顶之间)的延迟量；md,mw分别为干、湿空气的映射函数。

2.1 UNB3模型

UNB3对流层延迟模型由新布伦瑞克大学开发，在实际应用中它不需要测量本地的气象参数。UNB3对流层天顶延迟模型[7]为

(3)

(4)

式中：Φi+1，Φi为与Φ相差最近的格网大地维度；t为年积日；ξ为个参数的插值。

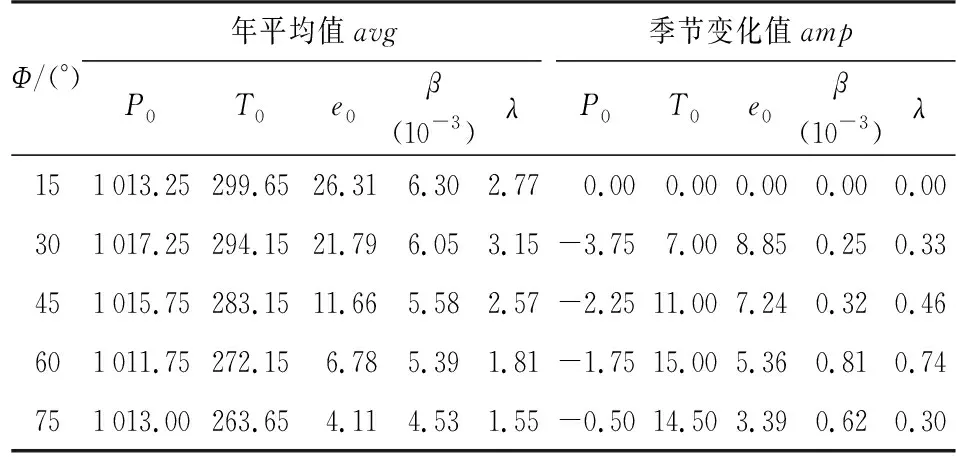
表1 UNB3对流层天顶延迟模型中的气象参数格网值

UNB3对流层延迟模型中的映射函数采用Niell模型[7]。该模型与各种气象参数变化无关，取决于卫星高度角、测站高程、测站纬度和年积日(一年中的第几天)等参数。同对流层天顶延迟模型一样，映射函数也采用干、湿两种映射函数模型。Niell干、湿项延迟映射函数模型为

(5)

式中：H为用户高程(m)；E为卫星高度角(rad)；ag=2.53×10-5；bg=5.49×10-5；cg=1.14×10-3；ad，bd，cd，aw，bw，cw分别为模型系数，可从表2和表3中插值得到，干项插值公式同式(4)，湿项插值公式为

(6)

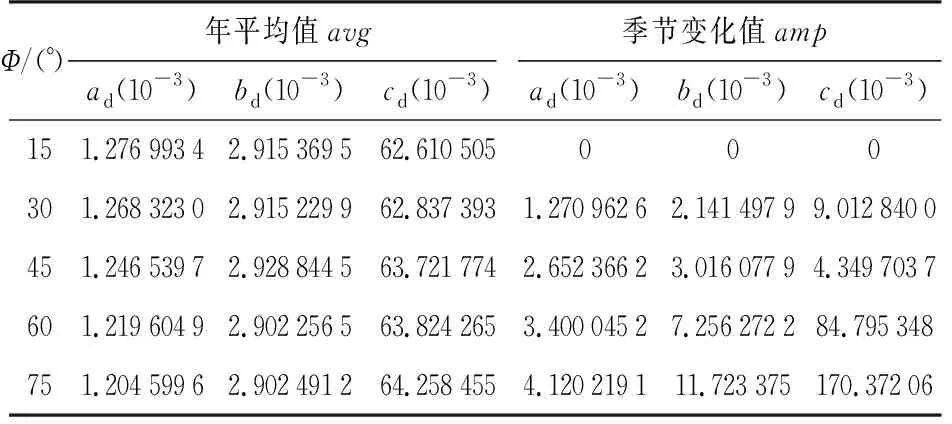
表2 UNB3对流层天顶延迟干项映射函数模型的系数格网值

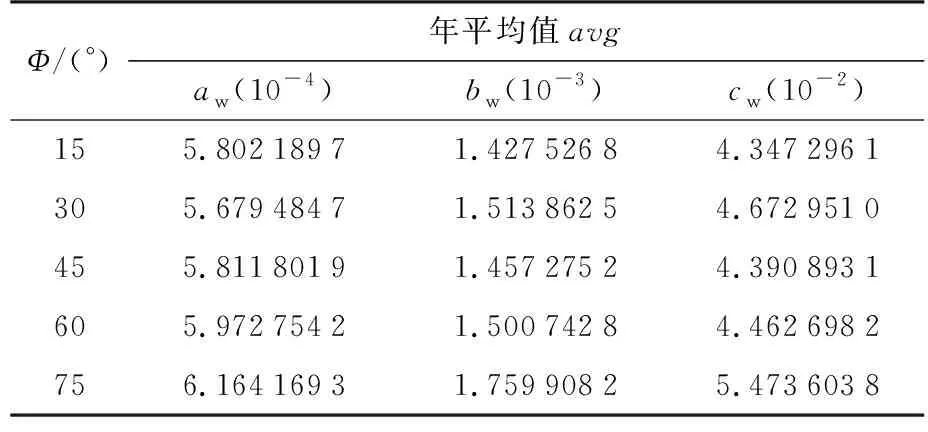
表3 UNB3对流层天顶延迟湿项映射函数模型的系数格网值

2.2 Hopfield模型

Hopfield对流层延迟模型由Hopfield提出，它是以全球的气象探测资料为基础得到的，在应用中需要测量本地的有关气象参数。Hopfield对流层天顶延迟模型[8]为

(7)

式中：H为用户高程(m)；T0，P0，e0分别为测站的大气温度(K)、气压(hPa)、湿度(hPa)；Hd,Hw分别为干、湿大气顶高度(m),它们可由式(6)计算得到。

(8)

Hopfield干、湿项延迟映射函数模型为

(9)

式中，E为卫星高度角(°)。

2.3 Saastamoinen模型

Saastamoinen对流层延迟模型于1973年提出，它是以测站维度、高程、观测高度角、干温、水汽为变量的函数，在应用中需要测量本地的有关气象参数。Saastamoinen对流层天顶延迟模型[9]为

(10)

式中，T0，P0，e0分别为测站的大气温度(K)、气压(hPa)、湿度(hPa)；Φ为测站处的大地维度(rad)；H为用户高程(m)；f(Φ,H)为地球自转所引起重力加速度变化的修正，f(Φ,H)=1-2.66×10-3cos(2Φ)-2.8×10-7H。

Saastamoinen干、湿项延迟映射函数模型与Niell干、湿项延迟映射函数模型相同，如式(5)所示。

3 对流层延迟仿真计算与分析

为了比较3种对流层延迟改正方法的精度，利用郑州地区2016年1,4,7,10四个代表月(分别代表冬、春、夏、秋四个季度)的实测气象探测资料进行计算。根据一般情况，假设对流层最大高度为60 km，并假设北斗卫星的高度角分别为1°，3°，5°，7°，10°，15°，20°，25°，30°，35°，40°，45°，50°，55°，60°，65°，70°，75°，80°，85°，90°。将3种对流层延迟改正方法与利用高精度电波射线描迹法计算得到的折射误差相减，得到的结果如图1所示。其中R-H，R-S，R-U分别表示射线描迹法与UNB3，Hopfield和Saastamoinen对流层延迟改正模型计算得到的折射误差之差。

从图1中的结果可得到一些结论： 1)随着卫星仰角的增加，UNB3，Hopfield和Saastamoinen三种对流层延迟改正模型的精度逐渐趋于接近，当仰角大于30°以上时，3种改正模型的精度与精确射线描迹法等同。这是因为随着仰角的增大，电波经过对流层的距离减小，大气引起的对流层延迟逐渐减小的缘故。2)当卫星仰角较小时，3种改正模型的精度中，Hopfield模型精度最差，Saastamoinen模型的精度最高，UNB3模型的精度居中。Saastamoinen与UNB3模型相比，尽管两个模型都采用相同的映射函数，但是UNB3模型用到的相关参数是由全球参数统计得到，不需要当地的实时气象参数，而Saastamoinen模型的相关参数中需要测量本地的有关气象参数，更接近实际大气环境，因此其精度高于UNB3模型。Hopfield模型尽管也采用当地的实测气象参数，但是一是由于它采用的映射函数的阶数较少而产生一定的延迟计算误差，二是由于其中的干、湿大气顶高度公式是由国外相关气象参数得到，与我国统计出来的公式也有一定的误差，这两种原因可能是该模型精度较差的缘故。3) 3种模型的精度在7月份比其他3个月份的精度都差，这是因为7月份是夏天，湿度变化较大，而所有的对流层延迟改正模型中误差最大的就是湿度项引起的延迟。从这些结论中可以看出，在实际应用中，当卫星的仰角大于30°时，UNB3，Hopfield和Saastamoinen三种对流层延迟改正模型的任意一种都可较好地实现高精度的对流层延迟改正；当卫星仰角较小时，建议采用Saastamoinen对流层延迟改正模型。

4 结束语

随着北斗卫星导航系统应用领域的不断扩大，用户对其定位精度的要求也不断提高，这就对减小大气对卫星定位误差的对流层延迟改正模型的精度提出了更高的要求。这里通过计算和分析北斗卫星在各种仰角情形下UNB3，Hopfield和Saastamoinen三种常用对流层延迟改正模型的精度，有利于用户实际应用北斗卫星对对流层延迟改正模型进行选择。下一步准备利用我国近十年的全国气象数据，以及相关的天基测量数据，参考这3种模型建立的方法，建立精度更高、适合我国实际应用的对流层延迟改正新模型。