基于EMD和奇异值差分谱理论的列车齿轮箱故障诊断研究及实现

于泽亮，贺德强，谭文举，沈国强

（1.广西大学 机械工程学院，广西 南宁 530004；2.南宁轨道交通集团有限责任公司，广西 南宁 530025）

1 引言

齿轮箱作为列车驱动系统动力传递的重要部件，其故障或失效严重影响列车的平稳、安全及正常运行。但由于其工况恶劣复杂，长期承受着挤压、扭转、摩擦等力的作用，极易发生磨损、断齿等故障，齿轮箱一旦发生故障轻则造成列车临时停车和机破，重则危及列车行车安全。对机车齿轮箱进行工作状态监测与诊断，明确齿轮箱工作服役状态，实现齿轮箱由事后维修到视情维修的转变，因此，对列车齿轮箱服役的安全性进行预测与诊断尤为重要。

迄今为止，国内众多科研工作者对齿轮的故障诊断提出了多种不同的诊断方法，其中，从齿轮箱中提取故障特征信息，对齿轮箱进行状态检测、诊断技术的研究与开发取得了良好的结果。文献[1-3]通过小波分析方法判断机车轨道交通齿轮箱是否发生故障和异常，由于输入比较单一，导致诊断结果不佳，且在小波分析中如何选择小波函数是一个难点问题，故障信号用不同小波基分解产生不同的结果，很难提供决策依据。文献[4-6]为解决神经网络结构及参数的优化选择问题，提出基于神经网络的机车齿轮箱智能故障诊断方法。神经网络算法常停止于局部最优解，且算法的培训时间过长时，会出现过度拟合，常把噪音当做有效信号。另外，美国通用电气公司研究的电力机车齿轮箱故障排除的专家系统DELTA[7]，专家知识库缺乏，知识库可靠性和推广性差，无法表达成通用的知识规则。文献[8]研究了诊断齿轮故障的同步时域平均方法，对轨道交通齿轮箱故障和振动产生机理研究不透彻，没有进行系统深入的研究。经验模态分解（Empirical Mode Decomposition，EMD）在齿轮箱故障诊断中，运用最广泛、最有效的方法[9-10]。易于拾取时域、频域分析方法中的特征信号，适合提取弱信号与处理非线性、非平稳信号[11]；奇异值分解具有稳定性、比例不变形、理想的消噪等能力，与其他降噪方法相比，SVD方法不像小波分析那样分析如何选择合适的阈值函数和消失矩阶数的影响，它对多变频信号也可成功降噪，能最大限度的消除噪声，又保留了与故障信号有用的信息[12-13]。

在齿轮箱有故障发生时，信号的局部特征信息在不同IMF（Intrinsic Mode Functions，IMF）分量中具有不同的故障信息，故可以选出突出特征信息的某个特征IMF，通过计算和分析来判断齿轮箱发生故障的位置与类型[14]。但是，由于其他噪声的影响，从很强的噪声中提取故障特征频率是较困难的。所以应用SVD对某个含有故障频率特征的IMF分量应进行消噪，从而获得故障特征的波形，可以准确判断故障类型。经过EMD分解得到的IMF分量不含直流成分，有利于应用差分谱理论，为了避免齿轮箱振动信号分析带来的困难，故应用EMD和奇异值差分谱相结合的方法来诊断齿轮箱故障。

2 信号分析方法

2.1 EMD算法分解

EMD分解的振动信号所得到的IMF分量应该符合以下两个条件：

（1）过零点个数和局部极值点个数之差为零，或不大于1；

（2）由三次样本插值算法确定包络线的均值在任一点处都必须为零。

EMD分解步骤：

（1）利用三次样本插值函数将故障信号x（t）中局部极值点拟合成包络线[15]。则有：

式中：m1—上下包络谱平均值的差值；n1—上下包络线的平均值。

（2）通常情况下m1不是本征模态函数，重复上述步骤，直到循环 k 次，m1k满足 IMF 的条件 m1（k-1）-n1k=m1k，循环结束，可表示为 c1=m1k，c1为信号 x（t）的第一个 IMF 分量。

（3）将 c1从 x（t）中分离出来，得到：

对r1重复以上步骤可以得到c2，c2就是x（t）的第二个IMF分量，重复l次即可得到l个IMF分量，得到：

当rn成为一个常量或单调函数，EMD分解结束。得到：

因此，原始信号 x（t）分解成 l个基本模函数，IMF 分量 c1，c2，…，cl从低阶到高阶，分别代表信号频段从高到低不同，并且还具有波内调制的特性。

2.2 奇异值差分谱理论

奇异值分解（SingularValueDecomposition，SVD）的定义：一个实矩阵H∈Rm×n，其中元素是实数域或复数域，无论其行向量与列向量是否相关，必定存在一对正交矩阵U∈Rm×m和V∈Rn×n，使得：

式中：S∈Rm×n，0 代表零矩阵，q=min（m，n），且有：σ1≥σ2≥…≥

σq≥0，σi=（i=1，2，…，q），称为矩阵 H 的奇异值。

要对信号 B=（bk，b2，…，bq-1）构造汉克矩阵，才能用奇异值分解。构造汉克矩阵：

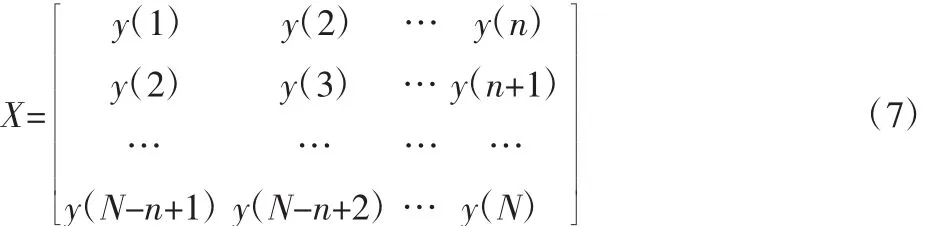
式中：1＜n＜N，N=m+n-1，X∈Rm×n。

构造奇异值差分谱：S=（σ1，σ2，…，σq），其中 σ1≥σ2≥…≥σq≥0，σi，i=1，2，…，q，是 hankel矩阵的奇异值，q=min（m，n）。定义：bi=σi-σi+1i=1，2，…，q-1

奇异值 B=［b1，b2，…，bn］称为差分谱。重构信号时，当选择重构奇异值个数较少时，少量有用信号可能会认为噪声；当选择重构奇异值个数较多时，可能残余大量噪声，故选用奇异值个数可以根据奇异值差分谱最突变点对应的位置决定，齿轮的故障诊断中，最大突变点一般反映由故障引起的齿面损耗、齿面胶合、疲劳失效或齿轮折断。故重构有用信号消除噪声，并进行Hilbert包络解调。从Hilbert包络谱中确定故障类型。

3 基于EMD与奇异值差分谱的列车齿轮故障诊断方法

首先将齿轮箱原始振动加速度信号进行EMD分解，然后选择得到的某个含有故障特征信息的，对其进行SVD消噪，信号重构，Hilbert包络解调，通过奇异值差分图谱观察故障频率，从而识别故障类型。该算法实现流程图，如图1所示。

图1 齿轮故障诊断流程图Fig.1 Flow Chart of Gear Fault Diagnosis

其诊断具体步骤如下：

Step1：原始振动信号通过EMD进行分解，得到8个不同振动信号的IMF分量。

Step2：提取包含信号故障特征频率的IMF分量，对其构建Hankel矩阵。

Step3：对hankel矩阵进行奇异值分解。

Step4：在同一坐标系中绘出奇异值与奇异值差分谱曲线。

Step5：由图谱中最大突变点，确定分量个数，重构信号，并进行Hilbert包络解调。

Step6：从Hilbert包络谱中确定发生故障类型。

4 实验研究

4.1 齿轮箱数据获取平台

为了获得齿轮箱实时数据，机车故障诊断车载子系统作为车载信息处理平台，其原理图，如图2所示。机车中安装机车运行故障诊断系统，其实物图，如图3所示。主处理器板卡，通过与防护记录器、无线通信板、网络接口板进行以太网通信，实现对TCMS（机车监控系统）、LKJ（机车运行监控装置）等车载设备信号的检测、处理及转发功能。

正在运行的机车齿轮上安装振动加速度传感器，通过RS485及以太网等接口与外部传感器检测到齿轮箱的信号通信，将检测到的信号保存到防护记录器内，通过以太网把信号从网络接口板传输到主处理器板，主处理器板把信号发送到无线通信板，当机车从远处靠近地面wifi基站时，通过wlan将无线通信板中机车走行部齿轮箱数据信号下载到wifi基站，从定向天线传输到附近服务器附近的基站。由此设计的齿轮数据获取平台能够实时获得齿轮故障数据，可以响应地面的数据传输要求，实现机车运行状态数据和故障信号的检测、本地存储和诊断。

图2 齿轮箱数据获取原理示意图Fig.2 Schematic Diagram of Data Acquisition Principle of Gear Box

图3 机车运行故障诊断系统Fig.3 Fault Diagnosis System of Locomotive Running

4.2 实验验证

提取原始数据的齿轮箱是HXD1C机车一对齿轮，模数为9，小齿轮为主动轮，其中从动大齿轮一个齿为断齿，电机额定转速N为1365r/min，小齿轮齿数Z1为17，大齿轮齿数Z2为106。根据以上参数，按照以下公式：

可得到大齿轮啮合频率fZ1=7.29 Hz，根据齿轮振动理论，当齿轮损伤时，其振动信号会发生调制现象，调制信号的模型为：

式中：A—被调制信号的幅值；X—啮合振动幅值；fn—缺陷齿轮所在轴的旋转频率；fz—缺陷齿轮的啮合频率，由此可以判断大齿轮发生断齿、点蚀、磨损或者胶合等故障。下面来判断

大齿轮发生的故障的类型，由公式：

可得到大齿轮断齿故障特征频率为fZ2=3.64Hz。齿轮断齿故障原始数据时域波形图和幅值谱，如图4所示。由于存在噪声信号，故障特征信息在波形图中无法提取，频谱中信噪比相对较低，特征频率淹没在噪声当中，不能看到明显的故障信息，故障齿轮对应的特征频率无法准确提取。

图4 故障齿轮波形及频谱Fig.4 Waveform and Spectrum of Fault Gear

为了提取故障特征频率，采用MATLAB进行编程，仿真软件为Matlab R2010a，原始信号进行EMD分解得到IMF分量谱，IMF分量谱是对信号的某一频段进行局部放大，提高分析精度，消除沉余特征信息，便于找到故障频率结果，如图5所示。可以看出有较为明显的冲击成分是imf 7分量，包含故障频率信息，且具有敏感性和稳定性，所以对imf 7分量求奇异值差分图谱。

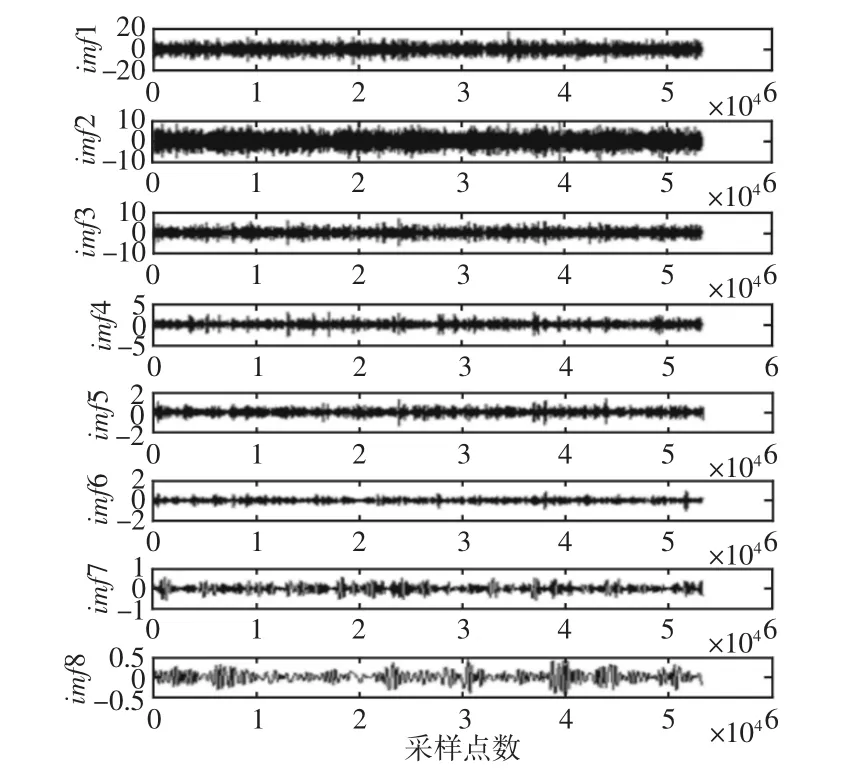
图5 EMD分解后的IMF分量谱Fig.5 IMF Component Spectrum After EMD Decomposition

将imf7分量作为研究对象，构造汉克矩阵，通过奇异值分解将imf7分量分解成一系列叠加的简单信号，且分解后信号值唯一。部分奇异值与奇异值差分谱数值，如图1所示。奇异值差分谱峰突变前段部分为有用信号，后面的都趋于零，根据最大谱峰奇异值差分谱可以自动确定重构有用分量个数，可以避免选择误差。

表1 部分奇异值与奇异值差分谱数值Tab.1 Partial Singular Value and Singular Value Difference Spectrum

为了突显变化规律，将奇异值序列和差分谱前50个点局部放大，如图6所示。奇异值序列峰值对应在第三个点，保留奇异值分解的前3个值，其余奇异值对应的分量为噪声，是无用信号为0，进行奇异值重构，对重构的信号进行Hilbert包络解调所得到的包络谱，如图7所示。可以很清楚的看到3.65Hz，7.29Hz倍频的谱峰，几乎没有干扰频率，与从动轮断齿故障特征频率3.64Hz的1倍、2倍频非常接近。可以断定该齿轮已经发生断齿故障，比较符合齿轮箱的实际情况，验证了此方法的可行性与正确性。

图6 奇异值和差分谱前50个点Fig.6 The First 50 Points of Singular Value and Difference Spectrum

图7 SVD重构后信号的Hilbert包络谱Fig.7 Figure of Hilbert Envelope Spectrum After SVD Reconstruction

EMD和Hilbert包络解调方法对齿轮箱进行故障诊断，如图8所示。原始故障信号经过EMD分解得到的imf 7分量进行Hilbert包络解调，虽然可以看到3.65Hz和7.29Hz频率存在谱峰，但还存在诸多干扰频率，容易造成误诊断。上述结果表明，EMD和奇异值差分谱，可以有效的改变信噪比，消除噪声信号的影响，通过对比可知，此方法可以有效提取齿轮的故障特征频率，故障诊断时间大大缩减，故障诊断性能较高。

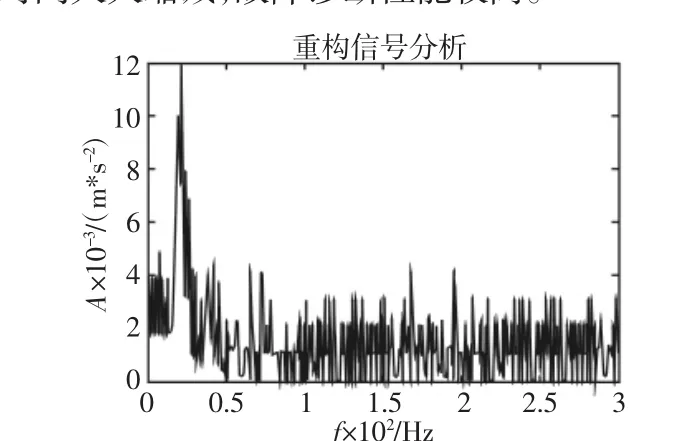
图8 imf 7分量的希尔伯特包络谱Fig.8 Hilbert Envelope Spectrum of Imf 7 Components

为了验证EMD和奇异值差分谱方法优于其他方法，分别建立了奇异值差分谱、EMD和Hilbert、EMD和奇异值差分谱三种齿轮箱故障诊断模型，试验中选取20组原始故障信号通过利用提取的特征向量进行齿轮箱故障诊断，仿真结果，如表2所示。由表可知，EMD和奇异值差分谱方法在齿轮箱故障诊断精度上比奇异值差分谱、EMD和Hilbert诊断方法有优势，因此EMD和奇异值差分谱方法更适合列车齿轮箱故障诊断。为机车齿轮箱故障诊断提供了理论基础，具有实际利用价值。

表2 三种齿轮箱故障诊断模型的结果对比Tab.2 Comparison of Three Kinds of Gear Fault Diagnosis Model

5 结论

针对列车齿轮箱的故障诊断和在线监测的功能实现，提出了一种基于EMD和奇异值差分谱的列车齿轮箱故障诊断方法，这种方法在对振动加速度信号进行分解与计算，剔除噪声干扰，从而找到故障频率，进行更为准确的故障识别，为了突显齿轮箱故障频率波形，更为准确地判断故障类型，建立了列车齿轮箱故障诊断模型，自动确定重构有用分量个数，克服搜索的盲目性，节省了故障诊断的计算量，提高了列车齿轮箱故障的诊断速度和准确性，体现该方法的优越性，具有广泛的应用价值。