铸造起重机金属结构的疲劳评定方法研究

魏国前 ，施棋博 ，刘 京

（1.武汉科技大学 机械自动化学院，湖北 武汉 430081；2.武汉工程大学 化工装备强化与本质安全湖北省重点实验室，湖北 武汉430205；3.宝武钢铁集团 武钢有限公司工程管理部，湖北 武汉 430080）

1 引言

铸造起重机是用于吊运熔融金属的一类特种起重机，是炼钢连铸工艺的主要设备之一。近年来，国内各大钢铁企业相继出现多起铸造起重机金属结构的疲劳失效事故，发现的疲劳裂纹具有数量多、尺寸长、部位多样化等特点。为了保障铸造起重机的安全生产，迫切需要一种针对其金属结构的有效疲劳评定方法。

文献[1]推导了桥门式起重机焊接箱形梁疲劳剩余寿命的计算公式，给出了各项疲劳参数的推荐值。文献[2]基于剩余寿命法，应用蒙特卡罗法对起重机焊接箱形梁的疲劳可靠度进行了仿真，给出了通用起重机焊接金属结构初始裂纹的均值和标准差。上述研究中没有考虑裂纹区域局部力学特性对疲劳行为的影响，计算误差较大。文献[3]通过模拟带有缺陷下的裂纹扩展，得到了典型工况下的应力强度因子理论值。这些研究从不同角度出发考虑了焊缝细节的局部应力效应，验证了局部应力效应对焊接结构疲劳性能具有不可忽略的影响，但其研究都是面向一般用途的焊接结构。

工程中对通用桥/门式起重机金属结构的焊接工艺和质量有一般性要求，但对铸造起重机则要严格很多，如所有超声波探伤须达到JB/T10559-2006《起重机械无损检测.钢焊缝声超检测》的I级要求，磁粉探伤符合JB/T6061-2007《无损检测.焊缝磁粉检测》的I级要求[4]。基于上述事实，常规的疲劳评定方法及其计算参数无法满足要求。针对铸造起重机金属结构，分析了主流的能够表征焊缝局部特性的应力概念及其对应的疲劳评定方法，开展了某在役铸造起重机的疲劳评定实例计算和分析。根据实际裂纹数据进反推计算，获得了适用于铸造起重机金属结构疲劳评定的S-N曲线以及适用断裂力学法的初始裂纹长度。

2 表征焊缝局部特性的应力概念

传统理论一般把主梁跨中截面作为疲劳薄弱点予以重点考虑，工程实践显示起重机金属结构的疲劳裂纹更多出现在结构形状发生突变的区域，例如主梁端部圆弧过渡区域[5]、主腹板和筋板连接区域[6]、马鞍形端梁的拐角区域等。这些部位不是传统意义的疲劳薄弱点，设计时常被忽略，但由于构造复杂，当移动载荷移动至其附近时，常常引入较大的局部应力效应，最终导致疲劳裂纹萌生。因此，起重机金属结构中构造形状突变部位的焊趾均为可能的裂纹源。

针对焊接结构的疲劳裂纹萌生特点，研究者们提出不同的应力概念表征焊接结构焊趾部位的疲劳性能，如名义应力、结构应力、缺口应力等。文献[7]提出的等效结构应力属于结构应力的范畴，能够反映焊趾的局部应力效应，构造过程中对有限元网格大小不敏感，评定时采用一条主S-N曲线描述不同的焊接接头形式。基于以上特点，采用等效结构应力作为铸造起重机金属结构疲劳评定的有效参量，基于主S-N曲线开展疲劳评定。

同时，断裂力学法采用裂纹尖端的应力强度因子作为主要控制参量，但在实际工程结构中，裂纹尖端的应力具有显著奇异性，很难利用有限元技术准确求解，因此多采用裂纹远端应力替代裂纹尖端应力计算应力强度因子，导致寿命估算误差很大。由于等效结构应力的概念及其构造方法都是基于焊趾局部，采用基于等效结构应力强度因子的断裂力学法对铸造起重机金属结构进行疲劳评定。

3 焊接结构疲劳评定方法

3.1 基于等效结构应法的疲劳评定

等效结构应力法[8]认为垂直焊趾方向的力以及绕焊趾方向的力矩是疲劳破坏的主要驱动力，因此在系统坐标系（x，y，z）下提取焊趾处节点力 F 和力矩 M，并向局部坐标系（x′，y′，z′）进行变换，得到变换后的节点力F′和力矩M′。基于平衡原理，等效为单元边线上的线载荷和线力矩，如式（1）所示。采用膜应力和弯曲应力计算焊趾处结构应力：

式中：σm—膜应力；σm—弯曲应力；σs—结构应力—线载荷—线力矩。

考虑板厚、载荷等因素进行修正，得到焊趾处等效结力σess。以焊趾处等效结构应力变程作为控制指标，结合主S-N曲线进行疲劳评定，公式如下：

式中：Δσess—等效结构应力变程，应该说明，工程中一般采用破坏率为50%的中值主S-N曲线，其中，A=12.18545，B=-3.05585。

3.2 基于断裂力学法的疲劳评定

断裂力学法认为焊接结构存在初始裂纹，并通常将其视为表面裂纹。该裂纹在载荷作用下沿表面方向和板厚方向同时扩展，并形成裂纹面，通常可表述为半椭圆形。图中：2c—表面方向的裂纹长度；a—板厚方向的裂纹长度。因裂纹表面方向的长度容易观察和测量，一般将其作为已知参量。理论研究中通常认为裂纹以同心半椭圆方式扩展，当裂纹扩展至板厚一定深度时，板材不再具有抵抗裂纹沿板厚方向扩展的能力，此时把裂纹作为贯穿裂纹，并只沿着表面方向扩展。

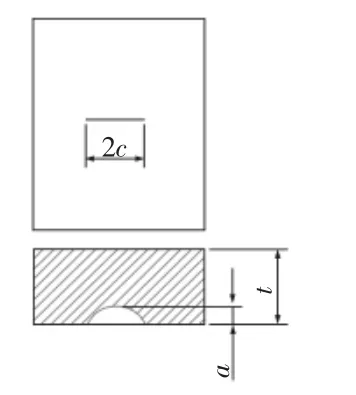
图1 半椭圆表面裂纹Fig.1 Semi Elliptical Surface Crack

疲劳裂纹扩展过程可以采用Paris模型进行描述，表达式如下：

式中：a—裂纹长度；N—裂纹扩展寿命；C、m—材料常数；ΔK—应力强度因子变程。

半椭圆表面裂纹沿厚度方向扩展的可按下式计算[10]：

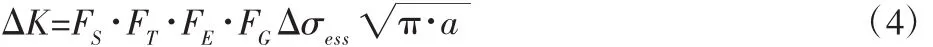
式中：Δσess—裂纹尖端的等效结构应力变程；FS—自由面修正系数；FT—有限板厚或宽度修正系数；FE—裂纹形状修正系数；FG—几何修正系数；a—裂纹深度。

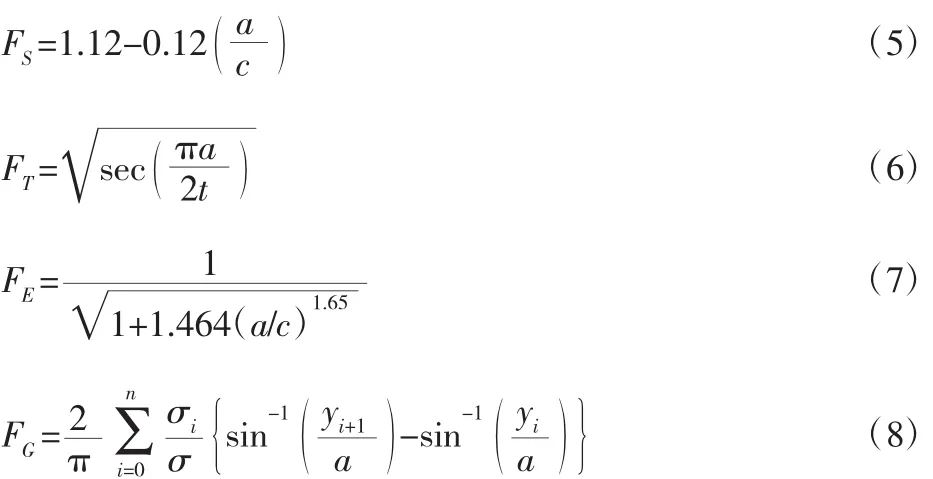
式中：a—裂纹深度；2c—表面裂纹长度；t—母材板厚；σi—沿厚度方向0≤yi≤t）处的弯曲应力；σ—表面弯曲应力，其中σ

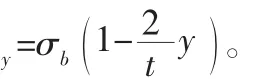
表面裂纹贯穿板厚后，成为贯穿裂纹，此时ΔK按下式计算：

式中：Δσess—裂纹尖端的等效结构应力变程，半椭圆裂纹计算此处a为表面裂纹长度的一半。

4 实例分析

4.1 问题描述

某炼钢厂从国外整体引进了1台450t×21.4m铸造起重机，1995年正式投入使用，2004年初该起重机金属结构上出现多处肉眼可见裂纹，多数裂纹发生在马鞍形端梁的内弯处，其中以靠近转炉侧（北端梁）的情况更为恶劣。几乎所有的裂纹都从角焊缝焊趾扩展到端梁腹板母材上，最长裂纹达到272mm。主要裂纹部位和长度，如图2、表1所示。

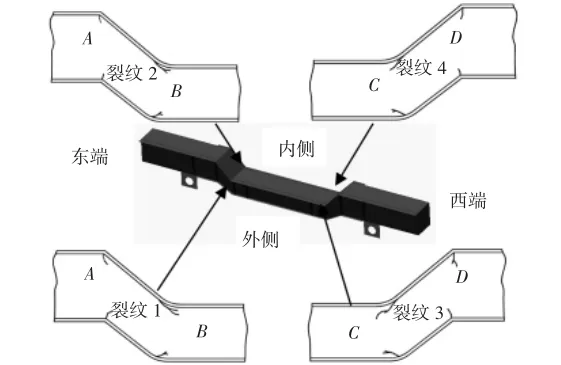
图2 北端梁裂纹位置示意图Fig.2 Crack Position in North End Beam

表1 铸造起重机裂纹所在部位及长度Tab.1 The Location and Length of the Crack in the Casting Crane

从表1可看到，北端梁上的裂纹比南端梁上对应部位的裂纹更为恶劣和危险。因此，针对北端梁上、下盖板与内、外侧腹板的4条主要焊缝，分析等效结构应力变程沿焊趾曲线的分布状况，基于主S-N曲线计算疲劳寿命；基于等效结构应力计算裂纹尖端的应力强度因子变程，以其为控制参量，基于断裂力学法计算疲劳寿命；对比起重机运行实测数据，分析2种方法的计算结果。

4.2 基于等效结构应力法的疲劳评定

起重机金属结构的各类薄板构件（如盖板、腹板、筋板等）大多采用板单元进行模拟，实际焊缝往往对应板单元的交线。求解等效结构应力时，需要提取有限元模型中焊趾处的节点力，因此必须保证焊趾曲线上分布有一系列节点。在同一条焊缝的2条焊趾曲线之间增设1层壳单元，用以模拟角焊缝。由于端梁结构较大，如图3所示。为控制有限元网格模型的整体规模，将非焊缝区域的网格尺寸设为80mm，焊缝区域则采用两次过渡方式。

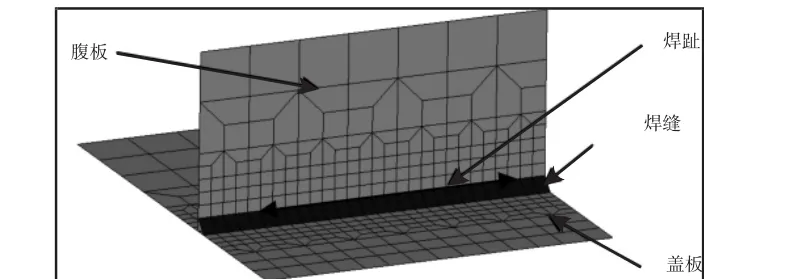
图3 壳单元模拟焊缝及网格过渡示意图Fig.3 Shell Element Simulation of Weld and Grid Transition

采用有限元软件ANSYS12.0求解，建立表2中两种工况，求解4条主要焊缝腹板侧焊趾曲线的等效结构应力变程，如图4、图5所示。北端梁下盖板与腹板连接焊缝焊趾曲线的等效结构应力变程曲线，如图4所示。北端梁上盖板与腹板连接焊缝焊趾曲线的等效结构应力变程曲线，如图5所示。

表2 铸造起重机工况Tab.2 The Working Condition of Casting Crane

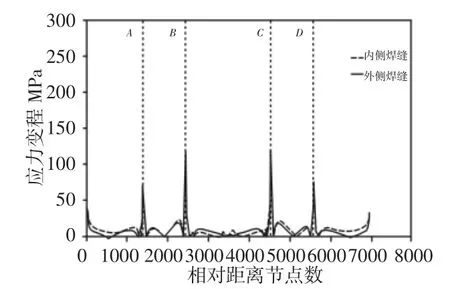
图4 下盖板与腹板连接焊缝焊趾曲线的等效结构应力变程曲线Fig.4 The Equivalent Structural Stress Range of Weld Toe in the Bottom Plate and Web

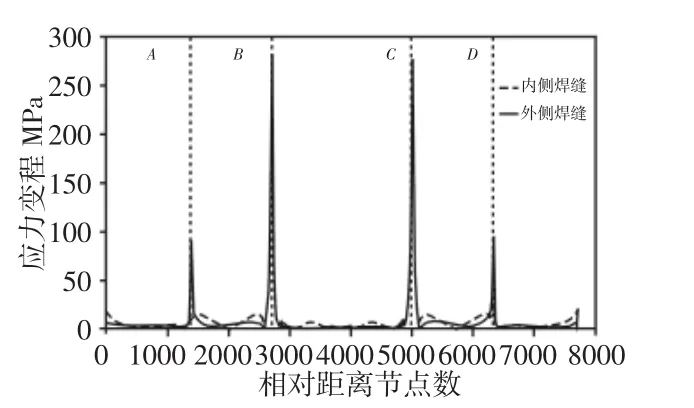
图5 上盖板与腹板连接焊缝焊趾曲线的等效结构应力变程曲线Fig.5 The Equivalent Structural Stress Range of Weld Toe in the Top Plate and Web

从图4和图5可以看出，所有4条焊缝的等效结构应力变程曲线具有相似的分布规律，4处尖峰值分别对应焊趾曲线上的A、B、C和D4处位置，其中，A点对应东侧外弯截面，B点对应东侧内弯截面，C点对应西侧内弯截面，D点对应西侧外弯截面，这4个截面均为端梁结构的构造形突变处，其等效结构应力变程值统计，如表3所示。根据表3分析得到，上焊缝焊趾处的等效结构应力变程值均大于下焊缝焊趾处的对应值；外侧腹板焊缝焊趾处的等效结构应力变程值均大于内侧腹板焊缝焊趾处的对应值；在同一条焊缝焊趾曲线上，内弯处的等效结构应力变程值均大于外弯处的对应值。因此，上盖板与外腹板连接焊缝的2个内弯处为最危险部位，这个结果和实际情况相符。

表3 北端梁内弯焊缝焊趾的等效结构应力变程Tab.3 The Equivalent Structural Stress Range in Weld Toe of the North End Beam Internal Bending

由表3可知等效结构应力变程最大值出现在C点处，值为271.89MPa，对应于上盖板与外侧腹板连接焊缝西端内弯部位，由表1可以看到，该处具有最长裂纹272mm，因此，等效结构应力法能够准确预测焊缝焊趾的疲劳危险点以C截面为例，将等效结构应力变程最大值带入式（2），计算寿命为56319次。考虑该铸造起重机实际情况，除去定期检修时间，1年工作350天，1天工作3个班，共计51个工作循环，计算寿命则为3.16年，与实际寿命相比，误差为64.89%。

4.3 基于断裂力学法的疲劳评定

同样以C截面为例，将该处初始裂纹看做半椭圆表面裂纹，初始裂纹表面长度取为2c=0.5mm[1]。按平均形状比a/c=0.75[10]，则a=0.1875mm。参照文献[9]，认为表面裂纹扩展至板厚78%时转变为贯穿裂纹，由于端梁腹板板厚为16mm，板厚方向的裂纹转变长度为12.48mm，此时裂纹沿表面的长度为33.28mm。该铸造起重机金属结构材料为Q345，取材料属性C=2.19×10-13，m=3.33[11]。由式（3）～式（8）算得裂纹沿深度方向扩展寿命为3.31年，由式（3）、式（9）算得裂纹沿表面扩展寿命为0.44年，总寿命为3.63年，与实际寿命相比，误差为58.78%。

4.4 SN曲线的确定及初始裂纹长度的确定

采用上述两种方法对铸造起重机金属结构进行疲劳评定，两种方法计算结果接近，表明这两种方法在起重机金属结构疲劳评定中具有相近的计算精度。结合文献中上述两种方法的应用情况，可以认为它们可以适用于一般的起重机金属结构疲劳寿命评定。同时，实例中这两种方法的计算寿命和实际寿命均有较大偏差，原因在于这两种方法的常规参数取值（S-N曲线表达式的系数、初始裂纹长度等）不适用于铸造起重机金属结构这一特殊对象。考虑不同的破坏概率值，对式（2）所示的S-N曲线进行计算，计算结果，如表4所示。

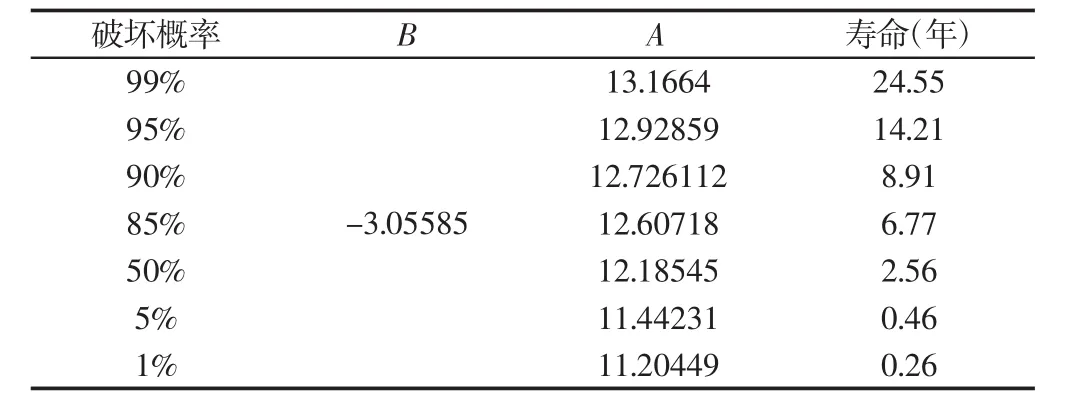
表4 S-N曲线参数及寿命Tab.4 The Paramter of S-N Curve and Life

铸造起重机的焊缝质量较高，具有较高的存活率，因此在疲劳评定时宜采用破坏率较高的S-N曲线。由表4可以看出，根据90%的S-N曲线计算得到的寿命为8.91年，略小于实际寿命9年，因此可以将该S-N曲线作为铸造起重机金属疲劳寿命评定的适用曲线，其计算结果偏保守。

同样，考虑到铸造起重机金属结构的焊缝质量较高，通常采用的初始裂纹长度2c=0.5mm偏大，不适用于铸造起重机金属结构。基于前述的断裂力学计算方法和基本参数，按9年考虑实际总寿命，反推得到初始表面裂纹长度为0.1396mm。因此，采用断裂力学法评定铸造起重机金属结构疲劳寿命时，建议表面方向的初始裂纹长度可以取为0.15mm，其计算结果偏保守。

5 结论

（1）采用基于中值主S-N曲线的等效结构应力法和基于等效结构应力强度因子的断裂力学法对铸造起重机金属结构进行疲劳评定，两种方法计算结果接近，可以认为它们是一般起重机金属结构疲劳评定的适用方法，并且具有相近的计算精度。

（2）现有的中值主S-N曲线和表面方向的初始裂纹长度0.5mm不适用于铸造起重机金属结构以及其它焊接质量较高的焊接结构。

（3）针对铸造起重机金属结构，建议在等效结构应力法中选用破坏率为90%的S-N曲线，或者在基于等效结构应力强度因子的断裂力学法中选用表面方向的初始裂纹长度为0.15mm，两种方法的计算结果偏保守，适用于结构的疲劳设计环节。