3-RPS并联机构SMC控制系统仿真

朱城伟，朱大昌，陈健伟，张荣兴

（江西理工大学 机电工程学院，江西 赣州 341000）

1 引言

并联机构由于其结构稳定，承载能力强，动态响应快和良好的位置精度等优点得到机器人领域的关注[1]，少自由度并联机构运动学、动力学研究相对简单，具有很强的灵活性，制造相对容易，在各个领域中更具有应用潜力，因而成为国内外学者研究较多的一类机构[2]。在少自由度并联机构中，目前研究最多的主要是3自由度并联机构，由于并联机构的Jacobian矩阵存在超越方程组，难以对其进行求解，通常是由螺旋理论求得Jacobian矩阵，但所得为方阵缘故难以对其进行控制仿真。采用矢量法以及并联机构微运动进行求解并联机构的Jacobian矩阵，可以避免在求解Jacobian矩阵所出现的超越方程的问题，从而得到并联机构的输入-输出连续映射方程组。

在并联机构在控制领域中，随着计算机技术的发展，人们利用人工智能的方法将数学模型和操作经验存入计算机建立控制系统模型，以便对整个机械系统进行控制[3]。然而控制方法是多样的，比如PID控制，模糊控制，神经网络控制等。但由于被控对象具有非线性，耦合性以及不确定性的特性，传统的控制器很难得到良好的控制。文献[4]提出用带有重力补偿的PID控制器对六自由度并联机器人进行控制，来消除机构的稳态误差提高控制精度。文献[5]分析6-PTRT并联机构的耦合特征，基于同步误差和系统的稳定性设计了光滑滑模控制算法，该方法可以抗拒并联机构支链之间的耦合效应，实现并联机构每个分支的协调，同步和更精确的运动。对于并联机构控制方面，大部分是基于6自由度，然而少自由度并联机构的控制研究较少。滑模变结构控制本质上具有良好的鲁棒性，瞬态响应速度快，对参数和外部扰动变化不灵敏。因此，滑模变结构控制被视为许多系统控制的有效途径，如不确定非线性系统，离散时间非线性系统与广义随机混杂系统[5]。由于柔顺并联机构是一个封闭式高度非线性耦合系统，其动力学模型的数学表达式十分复杂[6]。建立相对应的数学模型，工作量大，不易于实现，通过Matlab中的SimMechanics对系统进行建模，其优点可为多体动力机械系统及其控制系统系统了直观有效的建模分析手段[7]。采用SimMechanics Link接口，建立基于SolidWorks与SimMechanics的并联机构模型，并通过3-RPS并联机构的动力学方程，设计SMC控制器的切换函数与控制律，分别使用PID控制器与SMC控制器对并联机构进行仿真，对比并联机构动平台的轨迹跟踪误差曲线，证明所设计的滑模变结构控制的有效性。

2 3-RPS并联机构微运动分析

3-RPS并联机构由动平台、定平台和三条支链构成，如图1所示。支链包含转动副、移动副和球副。其中转动副连接定平台各个顶点，球副连接动平台各个顶点，转动副和球副之间由移动副连接。在定平台建立基坐标系O-xyz，同时在动平台上建立其动坐标系P-uvw，ΔA1A2A3为等边三角形，其边长为a，ΔB1B2B3为等边三角形，其边长为b，AiBi的长度为li。

图1 3-RPS并联机构Fig.1 3-RPS Parallel Mechanism

假定A1B1与OA1的夹角为φ1，A2B2与OA2的夹角为φ2，A3B3与OA3的夹角为φ3，AiBi基于基坐标系的坐标为：

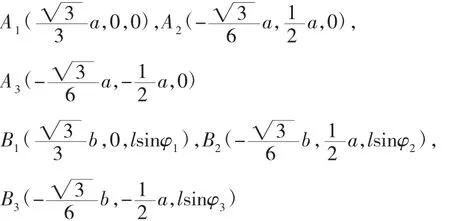
根据3-RPS并联机构具有两转动一平移的运动特性，假定3-RPS并联机构的动平台绕着下x轴转动α角，绕着y轴转动β角，沿着z轴移动距离d。

则绕x轴转动α角的转动矩阵为：

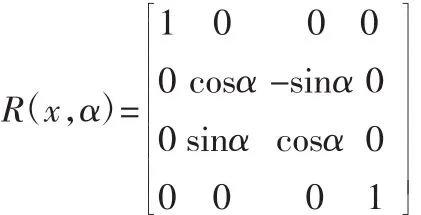
绕着y轴转动β角的转动矩阵为：

沿着z轴移动距离d移动矩阵为：

根据：R（α，β，d）=R（x，α）R（y，β）R（z，d）

可以得到3-RPS的旋转矩阵：

式中：s（）=sin（），c（）=cos（）下同。

由于3-RPS并联机构具有绕着x轴与y轴的转动和沿着z轴移动三个自由度，所以姿态反解是已知绕着x轴的转角α、绕着y轴的转角β以及z轴的移动距离d，求解各个杆长的变化。

由于并联机构采用微运动求解Jacobian矩阵，可以避免超越方程在矩阵中出现，同时求解得到的Jacobian矩阵属于非奇异矩阵，可用作并联机构的理论输入参考值。对于并联机构的微运动，动平台的位移应属于纳米级。故在进行计算的同时，有关于α、β、d的高阶次项趋近于无穷小。

综上所述：

3 3-RPS并联机构动力学建模

求解3-RPS并联机构的动能和势能，可以把并联机构分为动平台和支链两个部分[10]。可分别求出3-RPS并联机构动平台以及三条支链的动能及势能，然后再求出整体的动能及势能。

3-RPS 并联机构动平台的位姿参数为：q=［0，0，z，0，β，α］

根据并联机构动平台的位姿参数可以求出动平台的动能为：

式中：mplat—动平台质量；Ii—动平台的转动惯量。

动平台的势能为：Pplat=［0，0，mplat，g，0，0］Tq

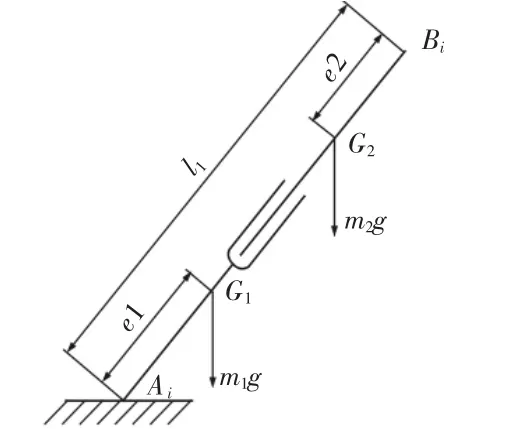
图2 驱动杆简图Fig.2 Diagram of Drive Rod

求解3-RPS并联机构3条支链的动能以及势能，可以把支链分为固定部分以及移动部分，如图6所示。支链的总长为li，固定部分的中心点为G1，与Ai的距离为e1，质量为m1，移动部分的中心点为G2，与Bi的距离为e2，质量为m2。

对此求导可得出支链的单位速度矢量为：

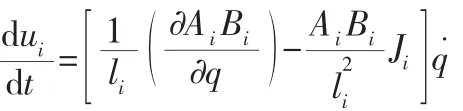
求出各个支链的位移矢量为：

根据拉格朗日运动学机械人动态方程可以写为：

4 建立并联机构的模拟框图

4.1 结构模型的建立

在Matlab中的SimMechanics中建立并联机构的模拟框图，由于3-RPS并联机构是由定平台、动平台以及三条铰链构成，其中三条铰链由转动副、移动副、球副组成的。可以使用SimMechanics中的刚体和运动副模块来描述各个物体之间的相互运动关系，如图3所示。

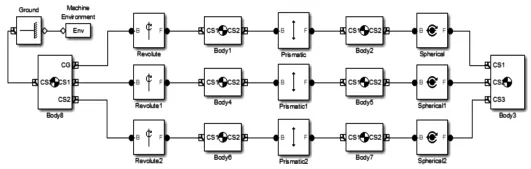
图3 3-RPS并联机构结构模型Fig.3 Structure Model of 3-RPS Parallel Mechanism

4.2 数学模型的建立

根据求出的雅可比矩阵，我们可以在Matlab中建立3-RPS并联机构的数学模型，因为3-RPS并联机构具有两转动一平移，则它的转动的变换矩阵依据 R（α，β）=R（x，α）R（y，β）可求得，而3-RPS并联机构的移动变换矩阵则为式（1）。

将之前求得的转动旋转矩阵与移动变换矩阵带入EulerXYZ中，同时在Desired1中给定3-RPS并联机构的输入信号，position matrix为位置矩阵，leg length为初始杆长矩阵，body_pts为并联机构动平台坐标矩阵，pos_base则为定平台坐标矩阵。

图4 3-RPS并联机构数学模型Fig.4 Mathematical Model of 3-RPS Parallel Mechanism

5 控制器的设计

5.1 PID控制器设计

PID控制器是一种广泛使用的工业控制器，，使用控制误差比例，积分和微分作用形成控制器的输出，并且这些组件的线性组合可以折衷系统响应速度和稳定性性的性能[9]。采用试凑法对PID控制器参数进行调整，使3-RPS并联机构达到最佳的运动轨迹，同样这也是最常用的方法之一，3-RPS并联机构PID控制器框图，如图5所示。其中，Integrator为连续时间积分，Gain为增益。

图5 PID控制系统框图Fig.5 Block Diagram of PID Control System

5.2 基于比例切换函数滑模变结构控制器设计

设 3-RPS并联机构动平台的期望位姿为qd（zd，αd，βd），系统的误差信号为e=q-qd，设计切换函数为：s=ce+e˙

式中：c=diag（c1，c2，c3），其中 c1，c2，c3均为可调参数。

由于 M（q）为正定对称阵，且矩阵函数M˙（q）+2C（q，q˙）对于任意 q，q˙，具有斜对称性，可得：

根据Lyapunov稳定性定理，可见所设计控制算法稳定，设计SMC控制器的Simulink框图。3-RPS的SMC控制器总图，如图6所示。

图6 SMC控制总图Fig.6 General of SMC Control

6 控制仿真结果

为了验证所设计的控制器的有效性，在Matlab的Simulink中进行仿真。用两种控制方法对3-RPS并联机构进行控制仿真，分别得出两种控制对于3-RPS的三自由度位移轨迹误差曲线，3-PRS与定平台相连的杆长为60mm，与动平台相连的杆长为60mm，两个杆长的可移动距离为40mm，三条支链与定平台的角度φ1=φ2=φ3=60°，定平台的边长为120mm，动平台的边长为60mm。

通过不断调节PID参数使得3-PRS并联机构控制达到最佳效果，此时PID控制器的参数为kp=48，kI=48，kD=48。不断调整SMC控制器模型中的ω和φ的值，直到控制曲线趋于稳定且无明显抖振现象时，此时ω=714，ψ=163，并通过在Simulink仿真中得出驱动杆的实际位移与理论位移的误差变化。

PID控制器与滑模变结构控制器对于3-RPS并联机构三条支链的位移轨迹误差曲线，如图7～图9所示。其中，虚ωΨ代表PID控制误差曲线，实线代表基于比例控制的SMC控制误差曲线。由图可知，清楚的反映了PID控制和SMC控制实际位移和理论位移的误差大小，SMC控制与PID控制相比的误差小，并且两者趋近于稳定误差的时间，SMC控制比PID控制的时间更短。

图7 支链A1B1位移误差Fig.7 Displacement Error of Branched Chain A1B1

图8 支链A2B2位移误差Fig.8 Displacement Error of Branched Chain A2B2

图9 支链A3B3位移误差Fig.9 Displacement Error of Branched Chain A3B3

7 结论

通过微运动建立3-RPS并联机构的输入-输出Jacobian矩阵，为机构运动学和控制仿真分析奠定了理论基础。并根据3-RPS并联机构的三维模型和动力学方程，设计了PID控制器和基于比例控制的SMC控制器，通过在Simulink中进行建模与仿真的结果表明，滑模变结构控制优于传统的PID控制，采用SMC控制器控制3-RPS并联机构调整时间短，误差小，并且响应速度快。控制效果好，基于比例切换函数的SMC控制器对于并联机构的控制是有效的。