6R机器人工具端的运动学建模及仿真

廖伟东，李锻能，王 强，廖 姣

（广东工业大学 机电工程学院，广东 广州 510006）

1 引言

打磨、焊接机器人需要在末端装夹磨具、焊枪等工具，而且工具工作点通常与机器人前一连杆坐标系存在沿X、Y、Z轴方向的偏置。机器人进行加工作业时，需要对工具的工作点进行路径规划。根据机器人不同的工作需要，获取机器人运动轨迹有在线示教再现法和机器人离线编程两种方法。

对于机器人运动学D-H法的建模，已有大量相关的研究，如文献[1-2]，其研究的末端控制点设置在机器人手腕或末端法兰盘中心，这种建立机器人运动学模型的方法，只能满足机器人在线示教编程的需要。对机器人离线编程，首先在工件3D模型上提取加工路径参数，生成机器人运动轨迹，然后需要控制机器人工具工作点的位姿。所以机器人控制点设置在手腕或末端法兰盘中心的方法，无法满足离线编程工作需求。研究的机器人控制点设置在工具工作点上，且相对于前一连杆存在沿X、Y、Z轴方向的偏置，在结构上不符合Pieper准则[3]，因此不能直接使用D-H法建立机器人工具端的运动学模型。

通过将工具坐标系从机器人连杆坐标系中独立出来，先使用D-H法求得机器人手腕坐标系相对于机器人基坐标系的位姿坐标，再通过平移齐次变换求得工具坐标系的位姿坐标。最后利用Visual C++、OpenGL图形库搭建仿真平台，对机器人运动学进行仿真验证。

2 机器人正运动学分析

2.1 建立机器人运动学模型

以三菱RV-13FL-D机器人作为研究对象，根据其连杆尺寸参数，建立的机器人连杆坐标系，如图1所示。再依据机器人连杆坐标系建立机器人D-H连杆参数表，如表1所示。

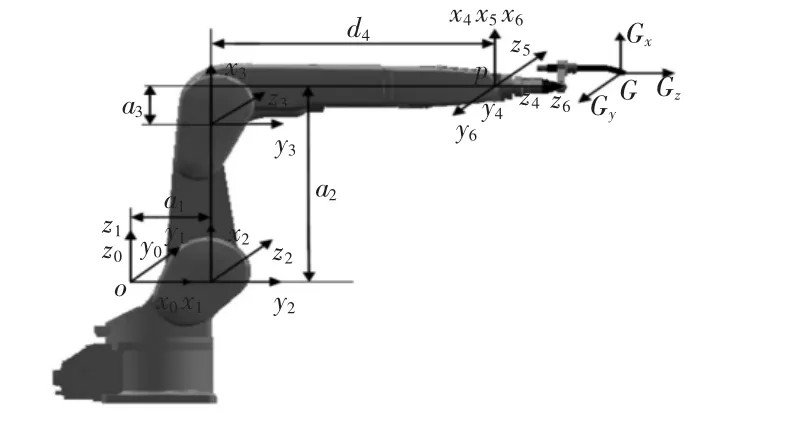
图1 机器人连杆坐标系Fig.1 Connecting Rod Coordinate of Robot

表1 机器人D-H连杆参数Tab.1 D-H Link Parameters of Robot

其中，连杆长度ai-1为zi-1与zi轴的距离；连杆扭角∂i-1为Zi-1与Zi轴的夹角；连杆转角θi为Xi-1与Xi轴的夹角；连杆距离di为Xi-1与Xi轴的距离。

2.2 机器人腕部运动学正解

机器人的正运动学建模，即是已知机器人六个关节的转角参数，求解机器人末端标志点相对于机器人基坐标系的位姿，根据表1的机器人D-H连杆参数，建立机器人相邻连杆齐次变换矩阵i-1Ti，如式1所示：

式中：Cθi=cosθi；Sθi=sinθi，以下类似。

这里的机器人手腕中心P点，与连杆6坐标系原点重合。所以机器人手腕坐标系｛P｝相对于与固定在地面上的机器人基坐标系｛O｝的位姿坐标，等于连杆6与连杆0的变换矩阵，所以可以求得机器人手腕坐标系｛P｝的正解，即如式（2）所示：

2.3 机器人工具端运动学正解

由于工具末端坐标点G相对与机器人手腕坐标系｛P｝，存在沿X、Y、Z轴的平移偏置，姿态与第六连杆保持一致，如图1所示。设点G相对与P点的相对坐标为（Δx，Δy，Δz）所以工具坐标系原点G相对机器人手腕中心点P的平移齐次变换矩阵PAG，如式（3）所示：

根据连杆坐标变换，求得工具坐标系｛G｝的正解：

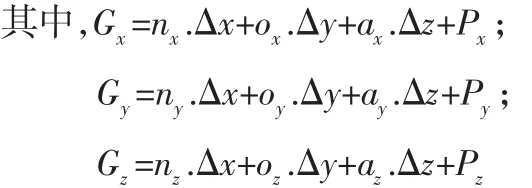
2.4 实现RPY组合变换O

由于通过TP变换矩阵表达机器人正解的方式不够直观，所以通常利用欧拉变换或者RPY变换以表达机器人末端的运动姿态。采用的是RPY组合变换表示运动姿态，即是，先绕X轴旋转ψ角，再绕基坐标系的Y轴旋转θ角，最后绕基坐标系的Z轴旋转φ角，得到：

因为 RPY（φ，θ，ψ）与OTP矩阵中的姿态参数相对应，所以可令两式中对应的元素相等分别求得θ、ψ、φ，如下：

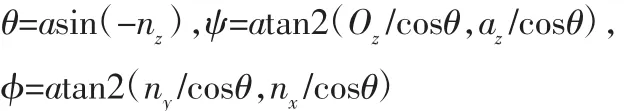
所以机器人工具坐标点G的正解OTG的RPY位姿表达式：

｛G｝=（Gx，Gy，Gz，ψ，θ，φ）

3 机器人运动学逆解

机器人运动学逆解的求解，即是根据已知的机器人工具坐标系｛G｝的位姿坐标，先求得机器人手腕坐标系｛P｝位姿坐标，然后反求机器人各关节角。由机器人连杆坐标系可以看出，其第4、5、6关节轴相交于一点，结构上满足Pieper准则[3]，可以采取封闭解法对机器人逆运动学进行求解。

3.1 机器人手腕位姿坐标求解

已知工具坐标系位姿｛G｝即OTG，反求机器人手腕位姿坐标｛P｝即0T6，由2.3节可知：

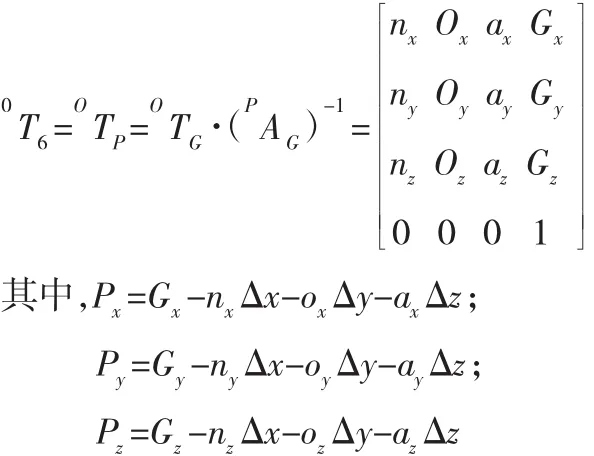
3.2 机器人关节逆解

（1）求解 θ1、θ2、θ3

（0T1）-1·0T6=1T6，利用左右两式（2，4）元素对应相等求得：θ1=atan2（Py，Px），θ′1=atan2（-Py，-Px）

因为2T5=（1T2）-1（0T1）-1（0T6）（5T6）-1，使得等式左右两边的（1，4）（2，4）元素分别对应相等，则可以求得：

将式（5）、式（6）分别乘以 w2与 w1，然后将两式相减，求得：

θ3=atan（a3w2-d4w1，a3w1+d4w2）

其中，w1=c2m-s2n-a2；w2=-s2m-c2n

（2）求解 θ5、θ4、θ6

使得式中左、右两侧的（2，3）元素相等，即可以求得：

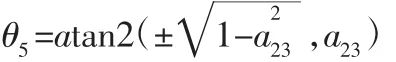
再利用式中左、右两侧（1，3）（3，3）元素分别对应相等求得：

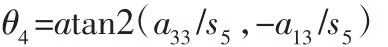
最后，使式中左、右两边（2，1）（2，2）元素分别对应相等求得：

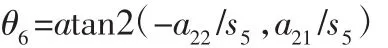
至此，已经求得了机器人全部六个关节转角：θ1，θ2，θ3，θ4，θ5，θ6的解。由于6R机器人最多具有8组封闭解[4]，而实际控制中只需要选择其中的一组解。在此先进行各组逆解关节范围的校核，排除超出关节运动范围的解，然后引入最佳柔顺解准则[4]如式（8），得出Ex最小的一组解，从而选取最佳的一组逆解。

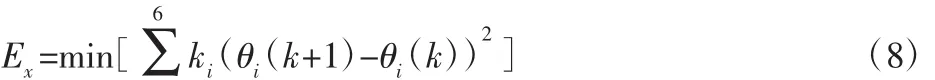
4 机器人工具端的轨迹运动仿真

利用Visual C++与OpenGL图形库搭建机器人仿真平台。通过读取机器人工具端经历的空间任意不共线三点的坐标，作为机器人空间圆弧轨迹规划示例。根据空间三点圆弧轨迹规划运算求取圆弧上的各个插补点坐标。然后在仿真平台上读入逆解求得的机器人各关节转角参数，进行机器人连杆坐标变换，最终实现机器人空间三点圆弧轨迹运动仿真。

4.1 机器人空间三点圆弧轨迹规划

设在笛卡尔坐标空间中有不共线的三点P1（x1，y1，z1），P2（x2，y2，z2），P3（x3，y3，z3），则在空间中一定存在一段通过这三个点的圆弧，设该圆弧的圆心为P0点，如图2所示。

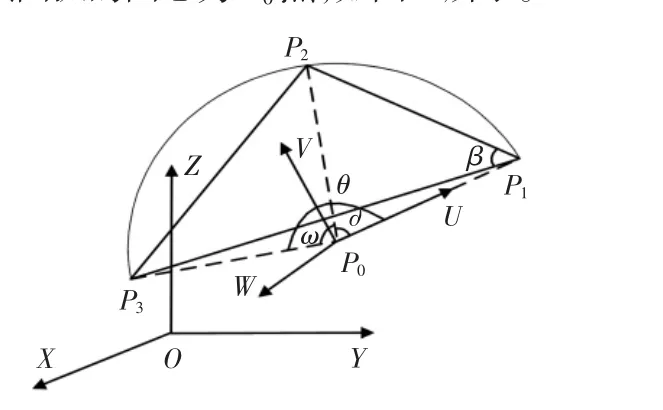
图2 圆弧轨迹规划示意图Fig.2 Diagram of Circular Trajectory Planning

首先求该圆弧的半径、圆心角、圆心坐标：根据两点间距离

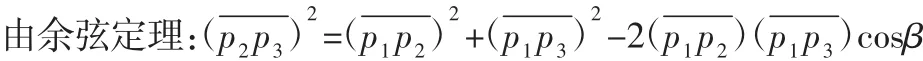
则圆周角：

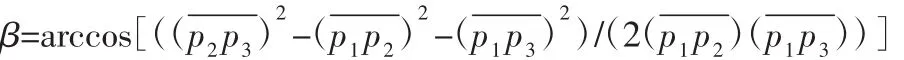
根据圆周角与圆心角的关系得：w=2β；同理可求得圆心角∂，则该段圆弧对应的圆心角：θ=w+∂

在P1P2P3平面中以圆心P0作为坐标原点，新建一个Po-UVW坐标系，如图3所示。求出Po-UVW在基坐标系O-XYZ下的变换矩阵A，就可以把三维空间圆弧转化为二维平面UPoV上的平面圆弧进行处理[5]。在UP0V平面上进行圆弧插补设插补周期为TS插补角速度为w，则可以求得插补次数：N=θ/（wTs）

则求得圆心角的时间函数：

θi＝w（iTs）；i=0，1，2，…，N

可求得UP0V平面上的圆弧插补点坐标为：

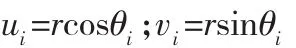
将UP0V平面上的插补点转换为基坐标系下的齐次坐标：

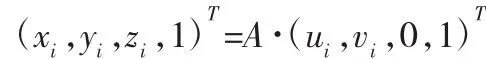
4.2 搭建机器人运动仿真平台

OpenGL（Open Graphic Library）是一个跨平台、功能强大、调用方便的底层3D图形库，已成为三维图形开发标准[6]。STL文件由多个带矢量方向的三角面片的定义组成[7]。机器人仿真系统是通过在Visual C++平台建立MFC单文档应用程序，调用OpenGL图形库函数建立的。利用OpenGL开源库，通过导入连杆STL文件的方式对机器人结构进行绘制。调用OpenGL库函数glRotatef、glTranslated，并且依照机器人连杆参数在函数中读入机器人各个关节角参数，进行机器人连杆坐标的变换，最终完成机器人仿真平台的搭建。

4.3 机器人工具端的圆弧轨迹运动仿真

通过“机器人示教”对话框，如图3所示。利用“关节模式”或“直交模式”点动控制机器人末端位姿，并在“直交坐标”、“关节坐标”对话框中，分别实时显示当前末端工具位姿的坐标值。在“插补运动”对话框，如图4所示。中分别读取机器人末端工具点历经空间不共线的三点P1、P2、P3的位置坐标，通过空间圆弧轨迹插补运算，可得到的插补运动轨迹，如图5所示。

图3 机器人示教对话框Fig.3 Dialog Box of Robot Teaching

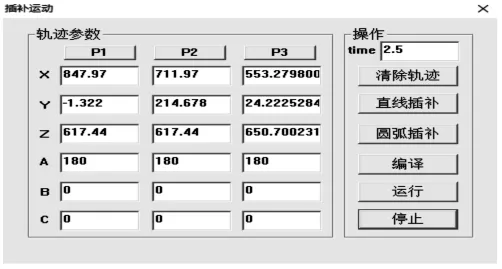
图4 插补运动对话框Fig.4 Dialog Box of Interpolation Motion

图5 机器人空间圆弧轨迹运动仿真Fig.5 Interpolation Motion Trail Simulation of Robot

将圆弧轨迹规划中得到的机器人工具末端插补点位姿坐标，代入机器人逆解运算求得各关节角的值。然后将其存储在thetaRecord数组中。通过SetTimer函数设置一个时间间隔为25ms的定时器，在OnTimer定时器响应函数中调用OpenGL库函数glRotatef，依序读入thetaRecord数组中的关节角数值，进行机器人连杆变换。通过系统函数InvalidateRect实时刷新机器人工作窗口，即可实现机器人自动连续的轨迹运动仿真。

5 结束语

针对机器人工具坐标系相对于前一连杆坐标系存在沿X、Y、Z轴方向的偏置，无法直接使用D-H法建立机器人工具端运动学模型的问题，研究了将工具坐标系与机器人连杆坐标系分离，利用D-H法结合坐标平移齐次变换的方法，建立机器人运动学模型，并求得面向工具坐标系的机器人运动学正、逆解。运用RPY组合变换表达机器人工具坐标的运动位姿，并给出了各个参数的代数解。提出一种余弦定理结合圆心角定律的机器人空间三点圆弧轨迹规划方法，避免了如文献[5]中坐标变换矩阵的求逆运算，大大简化了求解过程。通过VC++、OpenGL图形库，搭建机器人运动仿真系统，实现机器人空间圆弧轨迹运动的可视化仿真，使机器人运动学研究更直观。验证了机器人工具端的运动学模型和空间三点圆弧轨迹规划算法是具有可行性以及准确性的，为后续的机器人离线编程、动力学分析提供了可靠的依据。