汽车底盘测功机加载力控制仿真研究

李水良，史伟伟，耿伊方

（河南科技大学 车辆与交通工程学院，河南 洛阳 471003）

1 引言

底盘测功机是进行综合性能检测的一个重要的室内检测设备，通过对汽车在实际道路上的各种工况进行模拟，能对汽车的动力性、经济性、排放性、可靠性等进行检测[1]。汽车底盘测功机准确模拟车辆路面行驶阻力的关键是对测功机加载系统进行合理的设计，加载系统的控制效果直接影响测量的精度。与传统的开发模式不同，基于模型的设计将需求分析、设计、实现和测试4个阶段紧密联系起来。在统一的开发测试平台上，设计从需求分析阶段就开始连续不断的验证，从而在开发的初期就发现设计中的缺陷，且基于V型开发流程，开发人员在开发初期可以专注于算法设计和系统构建等方面的内容，软件代码采用一键式自动生成，保证代码质量的一致性，缩短开发周期，降低开发成本。

2 测功机电模拟加载原理

汽车在实际路面上的运行状况与在测功机上运行是有差异的，为了获得接近于实际的测试结果，应在测功机上再现汽车在实际路面上的行驶工况。通过建立底盘测功机模拟汽车行驶阻力方程，得出加载力的计算方程，从而实现汽车在真实路面上运行时受到的阻力模拟[2]。

2.1 汽车道路行驶阻力

车辆在路面行驶时，所受的阻力包括滚动阻力、空气阻力、坡度阻力和加速阻力分别用 Ff、Fw、Fi、Fj表示，汽车的驱动力与行驶阻力平衡方程[3]为：

式中：G—作用在汽车上的重力（N）；f—滚动阻力系数；CD—空气阻力系数；A—迎风面积（m）；u—汽车行驶速度（m/s2）；α—道路坡度；δ—汽车旋转质量换算系数；m—汽车质量（kg）；du/dt—行驶加速度（m/s2）。

2.2 汽车在底盘测功机上的阻力

汽车在测功机上运行时，所受到的力平衡方程如下：

式中：FR—电涡流机加载力；Fm—测功机内部机械阻力；Fg—驱动轮与滚筒之间的滚动阻力；FJ—惯性力（测功机的滚筒、轴系旋转部件产生的）；Fj—汽车的飞轮以及驱动轮转动惯量折算到车轮的惯性力。

2.3 测功机模拟汽车行驶阻力方程建立

汽车在实际路面行驶时，由传动系自身阻力造成的功率损耗与测功机上运行时是一致的，可不考虑。汽车在测功机上运行时，相对于地面是静止的，因此不存在空气阻力和车辆平移质量部分产生的加速阻力；同时车辆处于水平状态，不存在坡度阻力；从动轮静止不动，其滚动阻力也不存在。这些缺失的外部阻力都需要通过电涡流加载来模拟。通过控制和调节加载装置的加载力，使汽车在路面上的行驶阻力等于在测功机上的行驶阻力，从而模拟汽车在真实路面上的受力状况，这样在室内检测时结果才能与道路试验结果一致[4]。通过对比汽车在路面上与在测功机上的行驶阻式（1）、式（2），可求出准确的进行阻力模拟需满足如下方程：

得：FR=G（f+sinα）+0.6128CDAu+

从上式可以得出，在汽车型号以及坡度角确定后，已知汽车的滚动阻力系数f，汽车驱动轮与滚筒间的滚动阻力Fg，测功机的滚筒及轴系旋转部件的转动惯量IR，测功机的内部机械阻力Fm，对于试验的汽车，就可计算出加载装置应提供的加载力。上述阻力都是关于速度和加速度的函数，通过实验可以得到加载阻力与速度和加速度的关系式，从而可以计算出需要模拟的加载力。根据计算得出的加载阻力从而对加载装置进行实时的加载控制，就可以模拟汽车在路面上所受的阻力的变化过程，从而再现汽车在路面上的行驶状况。这里同时对汽车道路行驶阻力以及惯性质量进行了模拟计算，其测试结果从理论上分析将与在路面上的测试效果相同的。

在（4）式中包含有测功机内阻以及车轮在滚筒上的滚动阻力，可通过测功机上滑行试验测得。由试验测得某型号底盘测功机的内阻曲线，如图1所示。采用Matlab软件用最小二乘法拟合，经过拟合可得内阻与速度的对应关系为：

式中：Fm—某底盘测功机的内阻换算到滚筒表面的切向力（N）；

V—滚筒表面线速度（km/h）。

驱动轮在滚筒表面的滚动阻力系数可通过方程（6）确定：

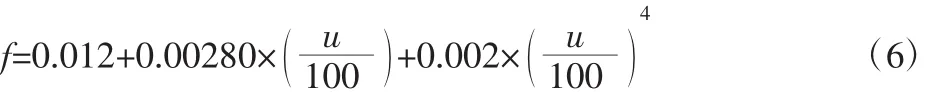
式中：u—车速（km/h）

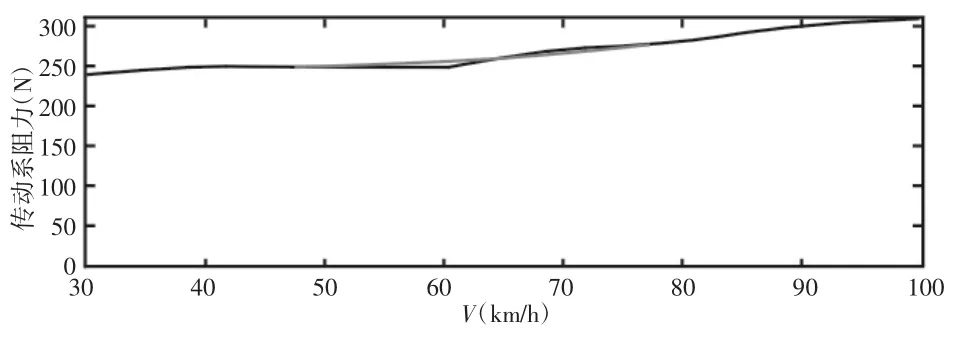
图1 某底盘测功机的内阻曲线图Fig.1 A Chassis Dynamometer Resistance Curve

2.4 电涡流测功器特性分析

忽略涡电流的电枢反映，同时不计磁滞损耗，假设定子线圈与转盘的导电和导磁系数均为一固定值，依据相关的电磁知识，可知电涡流加载装置的加载力矩的稳态模型如下[7]：

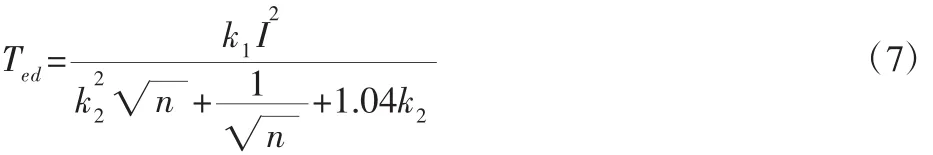
式中：Ted—电涡流加载装置的吸收扭矩（N·m）；I—励磁电流（A）；n—转盘转速（r/min）；k1，k2系数，与加载装置的自身的结构、材料以及工作温度等有关。

在进行动态分析时，电涡流机所加的电压引起的励磁电流变化可以近似表示为：

式中：It—励磁电流（A）；U—测功器阶跃输入电压（V）；t—响应时

间（s）；τ—时间常数 τ=L/R；L—等效电感；R—电阻。

电涡流加载装置本身存在阻值略小但电感、时间常数τ偏大的特点，因而加载力矩具有响应时滞的特点。Ted同时受到I和n的影响，则系统存在较强的耦合现象。

3 测功机控制方案及控制器设计

3.1 控制方案

汽车底盘测功机具有非线性、时变和强耦合等特点，风冷式电涡流测功机还存在扭矩响应速度慢的特点。针对这些特点，基于模糊控制理论与解耦控制理论，设计了模糊PID控制器和预测补偿解耦控制的电流转矩双闭环底盘测功机控制方案，如图2所示。

图2 控制系统框图Fig.2 The Diagram of Control System

底盘测功机的加载控制采用的是双闭环控制方式，外环是转矩环，内环是电流环。为了稳定涡流机的励磁电流，设计了内环，采取的是PI控制器进行闭环控制。采用预测补偿解耦控制以减小因转速变化而影响加载力矩的控制效果。

3.2 模糊控制器设计

模糊PID控制系统有模糊控制器和参数可调PID两部分。此控制系统主要是确定PID的kp、ki以及kd同e和ec之间的相应关系。运行时，模糊控制器依据e与ec的变化，经过相应的模糊推理得到、和，从而来对PID参数进行在线的调整，进而实现在不同的工况下对控制参数的要求[4-6]，因而与经典PID控制器相比，有更好的鲁棒性。

模糊PID控制器结构图，如图3所示。其输入为偏差e和偏差变化率 ec，经过模糊推理从而得出 Δkp、Δki、Δkd，从而将 Δkp、Δki、Δkd送入PID控制器，进而实现在线调整。按照常规模糊控制器进行设计。

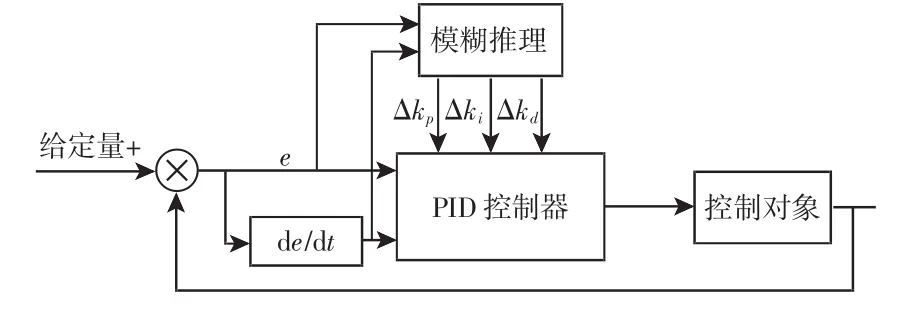
图3 模糊PID控制结构Fig.3 The Fuzzy PID Control Structure

模糊控制器采取两个参数输入，三个参数输出的设计结构。输入是偏差e以及偏差的变化率ec，输出是PID参数kp、ki与kd的修正值。偏差e与偏差变化率ec论域均采用［-3，3］，模糊子集采用｛NB，NM，NS，ZO，PS，PM，PB｝。输出 kp、ki、kd，论域和模糊子集设计同e和ec，各变量的隶属度函数均采取三角形函数。采取Mamdani算法，拟定49条模糊规则，如表1所示。去模糊化采取重心法。

表1 参数调整规则表Tab.1 Parameter Adjustment Rules Table

为将模糊PID控制器经自动代码生成的方式下载到在实际控制器中，考虑控制器运行效率问题，使用MATLAB自身的System test工具将模糊控制器转化为查表模块，这将提高系统的运行效率，同时也有利于节约系统资源。

3.3 反馈预测补偿解耦

由风冷式电涡流测功机自身特点，在车速偏低时，加载扭矩与车速间存在较强的耦合。解耦控制采取对扭矩控制器输出结果进行修正的方案。为简化解耦控制器的设计，采取反馈预测扭矩补偿的方案[7]。

预测补偿扭矩模型为：

式中：Tk—k时刻的输出扭矩；Δnk—k与k-1时刻的转速差。

4 建模仿真及结果分析

基于模型的设计是以Simulink为开发平台，可快速实现算法建模，在建模的过程中能够方便地检查和修改模型，具有很强的交互性。后期的代码自动生成，微控制器驱动集成、硬件在环测试等工作能够方便、快速的实现。

在SIMULINK仿真模型窗口中，创建加载力给定模块、模糊PID控制器模块以及驱动控制模块。模糊PID控制器，如图4所示。通过对kp、ki、kd进行在线自动调节，从而使系统达到控制最优。

图4 FuzzyPID控制器Fig.4 FuzzyPID Controller

晶闸管整流调压电路采用Simpowersystems建模，如图5所示。采用单向半控桥式可控整流电路，输入电压为50Hz、220V，改变触发器移相控制信号，从而调节晶闸管的控制角，改变输出的电压的大小。输出电压平均值为：Ud=0.45（1+cosα）当移相控制角为0时，输出最大电压0.9U=198V。通过系统自动控制移相控制角的大小从而调节输出电压的值，使其满足加载力的要求。

某型号底盘测功机滚筒直径是370 mm，基本惯量是500kg，某乘用车整车整备质量m=1080kg，车辆基准质量（整车整备质量+100kg）m0=1180kg，车轮半径r=340mm，空气阻力系数Cd=0.31，旋转质量换算系数δ=1.05，迎风面积A=2.2m2。测功内阻由式（5）确定，汽车在滚筒上的滚动阻力系数由式（6）确定。对加载装置进行模拟加载的过程中，应能满足从达到“目标驱动力×（1±10%）”时刻至进入“目标驱动力±20N”区间的时间不超过3s的标准的要求[8]

现设定电流PI控制器的kp=120、ki=1，在恒电流控制方式下，给定输入5V的输入电压（对应最大理论电流值为20A），可得系统响应曲线，如图6所示。电流能快速跟随给定信号，而且加载电流越小响应速度越快。对加载力控制，设定汽车速度为80km/h，加载装置需模拟的加载力FR=94.15N。从图7可知，此时的加载电流为1.12A，加载装置实际加载力能较好地满足理论给定值，测功机加载力控制误差在±4N范围以内，完全满足规定的±20N界限。

图6 电流加载响应Fig.6 Current Load Response

图7 加载力响应曲线Fig.7 Loading Force Response Curve

在进行上述的仿真验证后，为实现在现实环境中的控制，需进行定点化离散化处理，将控制部分自动生成嵌入式C代码。同时，为了验证生成C代码的优劣，进行了软件在环测试，仿真结果与图6，图7相同，说明C代码功能是可行的。通过移除被控对象的仿真模型，在输出端和传感器部分添加控制输出端口和AD转换等接口模块，从而实现与底层程序的连接，快速实现所需代码的生成。

5 结论

依据电涡流测功机的机械特性，采取转矩、电流双闭环以及模糊自校正PID的控制方案，解决了电涡流测功器自身存在的不足，实现了对理论加载力矩的良好控制，满足国标要求。采用基于模型的设计方法可以快速实现算法的验证，在得到正确的仿真结果后可轻松实现代码生成，从而进行硬件在环试验。