基于16S rRNA序列物种鉴定的改进向量空间模型算法①
祝 斌,亓合媛,马俊才1,
1(中国科学院 计算机网络信息中心,北京 100190)
2(中国科学院大学,北京 100049)
3(中国科学院 微生物研究所,北京 100101)
在过去的几十年中,随着生物学数据的大量累积,以及计算机技术、数学和生物学交叉学科的崛起,21世纪已经进入了云计算和大数据时代.云计算时代也为基因序列比对能够在较短时间完成提供了坚实的基础.物种鉴定是用来描述物种间近缘关系和进化层次的非常有用的一种工具.最初,物种鉴定常常基于单个基因序列或是很少的几个基因序列进行对比,这种方法虽然简单易行,但是由于横向基因转移(Horizontal Gene Transfer,HGT)、并系同源基因(Paralog)以及物种进化差异等因素的出现,这种方法受到了质疑.
基因测序方法在一定程度上解决了单基因序列比对出现的问题,保证了系统发育树的合理性.但是,与此同时,随着序列数据的增加,计算时间呈指数式增长(如图1所示),因此,计算效率成为了亟待解决的问题.
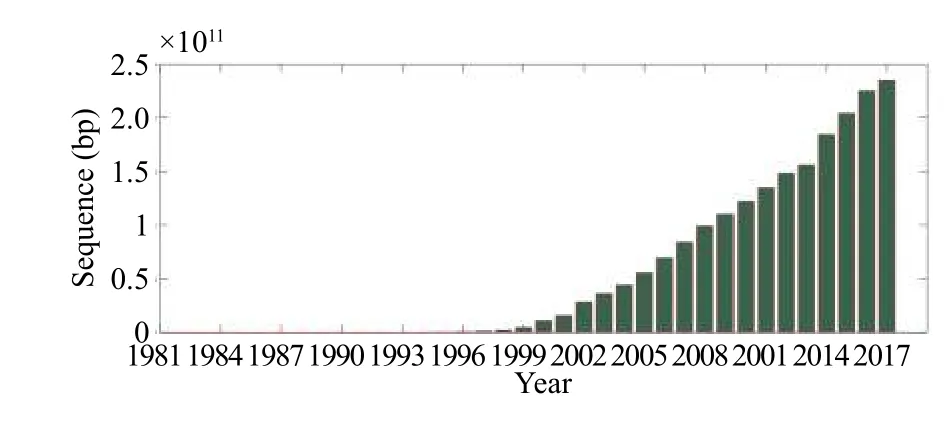
图1 Genbank数据库序列数目随年份走势图
近期,关于物种鉴定的方法逐步地出现了全基因组序列对比.在此期间,众多学者提出:比较两个完整的基因组意义并不大,原因在于:每个物种都有自己特定的基因含量和基因顺序,此外基因组的数量是不同的;另外,微生物的基因数据也是需要人工处理操作的,不同的实验室处理数据的不同会造成结果在一定程度上的差异,进而使得结果不具备更完整的说服力,非序列比对方法便应运而生.
非序列比对方法在计算效率上明显优于前者,操作也较简单,运算效率较高.近几年,关于非序列对比的方法也不断更新.目前比较常见的方法有:K串组份向量方法,(0,l)序列法,DNA Walk,压缩矩阵法,表示法,CGR方法,Nandy二维图形[1]等.近年的新兴算法在物种鉴定方面上的应用上不够广泛,在所有的非序列比对算法中,使用最为广泛且传统的算法为基于TFIDF检索技术的向量空间模型(Vector Space Model,VSM)算法,然而其物种鉴定的分类效果得不到保证[2],原因在于该算法没有借鉴到微生物的背景,因此无法消除在基因突变和物种进化的背景下,基因序列的噪音影响.因此,在确定非序列对比算法具备了提高运算效率的优点,以及向量空间模型算法在众多经典和最新的文献[3]中使用较为广泛的特点之后,为此,本文以如何改进向量空间模型算法,进一步达到提高运算效率和保证分类效果质量两方面为主要目的.
在众多生物系统发育相关性水平指标中,16S rRNA基因序列具有如下特征:
1)普遍存在于一切细胞内;
2)机体生理功能稳定且重要;
3)在微生物中含量高,且容易提取;
4)编码基因比较稳定;
5)序列相对保守;
6)相对分子量适中;
7)基因序列长度适中;
8)既含有高度保守的序列区域,又含有高度变化的序列区域.
基于以上的各个特点,16S rRNA 基因序列具备最佳的鉴定特征,是本文改进向量空间模型算法的应用数据,可以为物种鉴定打下坚实的基础.
综上,本文以16S rRNA 基因序列为应用对象,使用改进向量空间模型算法为核心,以达到快速分类和保证分类质量的研究目的.
1 背景及相关工作
分子生物系统发展史的出现以及基因测序方面的进步,大大加深了人们对物种进化的理解.因此,物种分类和鉴定在分子水平上的进步已经为微生物的分类提供了一个具有实用价值的工具.
目前分子系统发展史有两大重要研究成果:一是线粒体和叶绿体之间具有内生共体特性,二是目前为止,生物可划分为古生菌,细菌,和真核生物三个生物领域.然而,随着完整的微生物基因组数据的逐步添加,实验结果逐渐地对公众预期提出了质疑[4],在这一争议过程中,仍有几个实验试图从完整的基因组中推断出原核生物发展史.以上实验使用的方法包括利用基因含量[5],直系同源基因簇的存在/缺失值比例[6],父系树[7],保存基因对[8]等方法.然而这些方法最终都依赖于序列比对这一传统思路,到目前为止,还没有一种能够被广泛接受且用于从完整基因组数据中推断出系统发育树的方法.
此后,逐渐出现了非序列比对的方法[9],计算效率和结果都得到了广泛的认可,因此成为了除BLAST算法以外物种分类与鉴定方面不可或缺的方法.而向量空间模型(VSM)算法在众多前沿文献中使用的频率较高,由此可见,目前向量空间模型算法是非序列比对算法中构建系统发育树的主流算法.因此,对其算法的改进具有重大意义.
根据相关文献[10]的说明,截至目前,使用16S rRNA基因序列对物种进行鉴定和分类的项目有:美国的Greengenes,RDP核糖体数据库,以及韩国的EzTaxon.以上项目的核心基础仍是利用BLAST局部比对算法进行快速分类,输出初始排名结果,随后使用双序列全局比对,给出在参考样本数据库中与待测序列最为接近的排名序列,以此作为参考,对样本序列进行鉴定和分类.
根据前面的分析,我们发现,用于物种鉴定的主流算法仍是基于BLAST的序列比对算法,然而由于该算法出现计算量过于庞大,运算效率低以及资源消耗较高等问题,使用VSM方法能够有效地解决上述问题.
VSM算法的运算效率相比于BLAST算法更优,此特点解决了BLAST算法的核心问题,但该算法的不足之处在于其分类效果远远没有主流BLAST鉴定算法更为优越.因此,对VSM算法的改进就具有了现实意义,而改进的VSM算法可以作为物种鉴定的另一种有效工具方便科研人员参考和使用.
此外,经典文献[11] 提到的K-String组份向量算法在病毒[12],原核生物[13–17],真菌[18],叶绿体序列[19]以及人体的肠道元基因组[20]有了成功的应用.
综上所述,本文旨在对常用的VSM算法进行改进,将该改进VSM算法应用于基于16S rRNA序列的物种鉴定领域,达到运算效率和分类质量两方面的提高效果.本文后续的内容逻辑为:在第2节介绍两种VSM模型算法以及两种算法的区别,一种是基于TFIDF检索技术的VSM模型算法,另一种是借鉴经典文献[1]后的改进VSM模型算法.此外,本文还给出了改进VSM模型算法中遗传距离在巴拿赫空间下的等价替代公式,并给出了相关说明;同时,第2节给出本文为测试改进VSM算法运算效率和分类排名质量两方面效果所使用的数据集来源,以及对应的运算时间和排名效果结果汇总及相应分析;第3节是对接下来研究工作的讨论与未来展望.
2 VSM算法与改进VSM算法
2.1 VSM算法原理[21,22]介绍
本文将以16S rRNA基因序列分析为研究背景,介绍VSM在该背景下的操作流程.
一个物种16S rRNA基因序列文本,其碱基只有AGCT四种,将碱基序列划分为不同的K子串,那么此排列方式就有4K种可能,通过计算词频和逆文档频率,最终得到该16S rRNA序列文本对应的权重向量,维数为 1×4K.
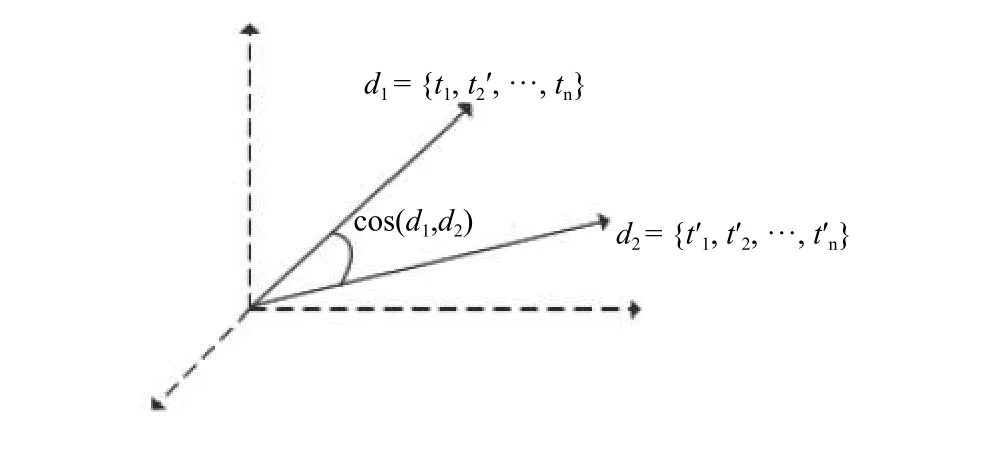
图2 序列相似度
图2中,每一项的权重都由词频和逆文档频率综合表示.
假设有N条样本序列,记为D={d1,d2,···,dN},词频fij表示K串词项wi在序列dj中出现的次数,ni为含文本w的数量,逆文本频率计算公式为:

其中,序列dj中词项wi的TF-IDF权重公式为:
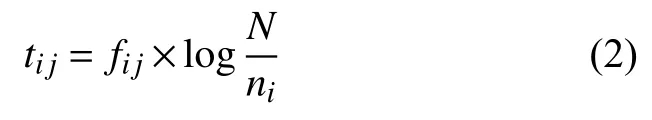
最后,样本序列相似度量值计算公式为:
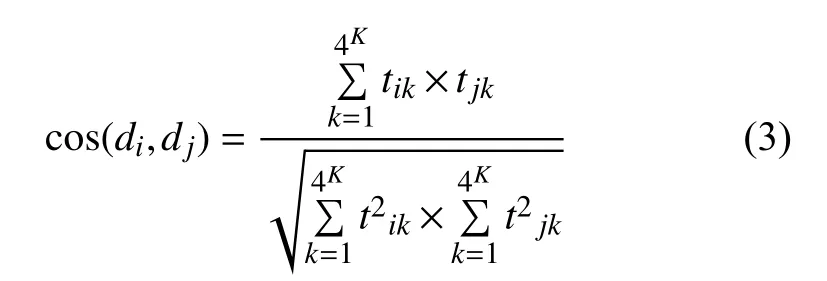
2.2 改进VSM算法原理介绍
该算法涉及6个步骤,将分别作出说明.
第一步.计算K串词项出现的频率.
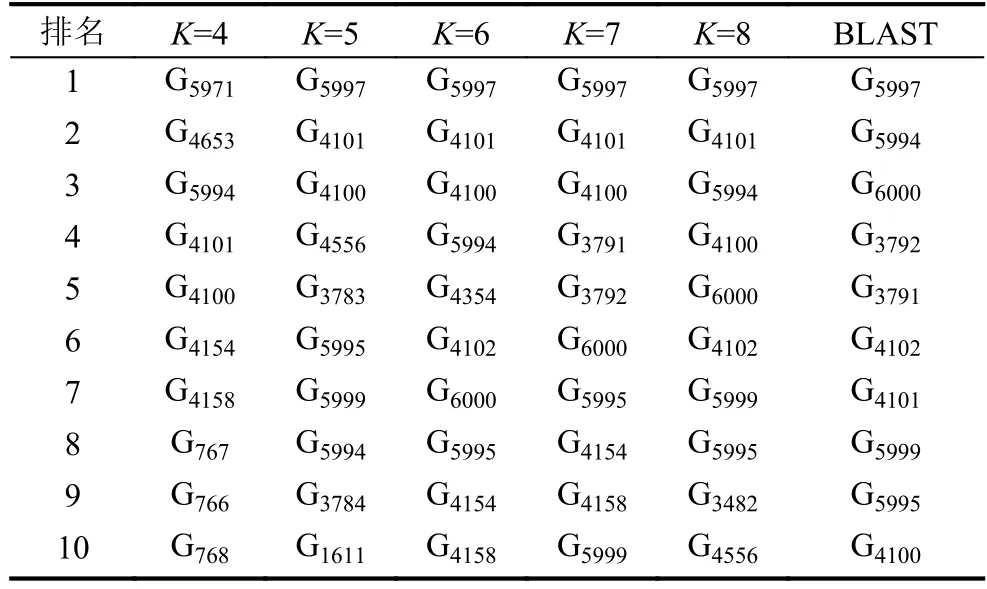
长度为L的16S rRNA序列 α1α2···αL,选取长度为K(K 第二步.计算随机突变背景下的噪音频率. 随机突变在分子水平上或多或少以随机的方式发生,而基因重组的选择决定了进化的方向.以上因素导致了一些K串词项产成了一定的随机性.为了还原该K串词项的原始频率,本文需要对此噪音进行刻画,根据最大熵原理的推导过程,我们得到了噪音频率公式: 第三步.计算修正后K串词项频率. 综合前两步,本文给出了修正后频率计算公式: 第四步.计算每一个16S rRNA序列修正后的特征向量. 将每一个可能的序列子串 α1α2···αK的频率作为一个物种的特征向量的元素.为了进一步简化这一个定义,我们定义ai为所有排列好的K子串中第i种子串类型对应特征向量中的第i个分量.这里i从1到4K循环.因此,我们可以得出对于16S rRNA序列A的特征向量: 以此类推,对于物种B,我们仍有特征向量: 第五步.计算各序列间的遗传距离. 这里同样以序列A,B为例,两序列间的遗传距离使用传统的夹角余弦进行表示,公式如下: 由公式(9)知,夹角余弦数值的取值范围为[–1,1].若将夹角余弦记做物种间的遗传距离,则有:两物种特征向量对应的遗传距离越大,说明两个物种之间的相关性越强;反之,遗传距离越小,说明两物种之间的相关性越弱.为了符合直观,表达相关性强,对应遗传距离小;相关性弱,则遗传距离大的说法,本文对此距离公式进行标准化修正,公式为: 第六步.计算待测样本与参考序列库之间的遗传距离,从小到大进行排序,输出前十名相关性最强的序列及其遗传信息,以辅助科研人员参考和进行物种分类和鉴定工作. 遗传距离的定义是计算分子生物学中一个重要环节.该距离的定义需要满足以下三个条件(记D(x,y)为两个物种间的遗传距离): 非负性:D(x,y)≥0,D(x,y)=0等价于x=y; 对称性:D(y,x)=D(x,y); 三角形不等式:任意三个物种z,x,y,距离恒满足:D(z,y)+D(y,x)≥D(x,y). 显然,在本文的第2.2节中的公式(10)符合遗传距离的定义.这里值得一提的是,夹角余弦公式使用的是内积空间下的2-范数.根据向量范数的等价性定理: 设||x||s,||x||t为Rn上向量的任意两种范数,则存在常数c1,c2>0,使得对一切x∈Rn,有c1||x||s≤||x||t≤c2||x||s. 以及极化恒等式:实线性空间上的内积和范数有以下关系: 综合上述内容,本文将公式(8)中内积范数进行重新定义,给出在1-范数和无穷范数下的计算公式,公式如下: 2.4.1 待测样本与测试数据集 本文所使用的16S rRNA样本序列数据,来源于(863计划,课题编号:2014AA021501)中通过质检工具pipeline筛选整理出的高质量16S rRNA基因序列参考数据库. 这里,本文从参考数据库中随机选取了8000条样本序列.其中,将前6000条为参考序列样本库,剩余的2000条作为待测样本进行测试. 为了简化名称,这里依次定义序列编号为G1,G2,…,G6000,G6001,…,G8000.其中,G1,G2,…,G6000为参考数据库,G6001,…,G8000为待测样本. 2.4.2 改进VSM算法运算效率与blast运算效率结果 结合第2.2节所述,可以发现,本文所选取的6000条参考样本序列文本可以通过改进向量空间模型算法进行计算,得出对应的6000个特征向量,是本实验的预处理阶段.因此,以上6000个特征向量的运算时间完全不需要计入该算法的运算时间,这也是该算法提高运算效率的一大优势. 这里,本文首先按照第2.2节所述的操作步骤逐一进行:(这里以K=4为例) 第一步.对前6000条16S rRNA参考样本序列G1,G2,…,G6000,逐一带入公式(6),计算出每一个序列文本对应的修正频率特征向量A1,A2,…,A6000. 说明.此阶段为数据预处理阶段,不占用算法计算时间;其中每一个特征向量的维数为:1×44即1×256. 第二步.i=6001,对待测样本Gi计算出对应的修正频率特征向量Ai. 第三步.计算Gi与G1,G2,…,G6000序列之间的遗传距离C(Gi,G1),C(Gi,G2),…,C(Gi,G6000),依次记为遗传距离d1,d2,…,d6000. 第四步.对上述6000个遗传距离d1,d2,…,d6000按照递增的顺序进行排序,输出相关性较高的前十条序列排名结果作为物种鉴定的参考初步排名结果. 第五步:i=i+1,直至计算至最后一个待测样本G8000. 说明1.其中第2,3,4步为一个待测样本与6000条参考样本序列G1,G2,…,G6000的整个运算过程,其花费时间也为该改进向量空间模型算法的单个样本进行排名输出的运算时间. 说明2.本文将i从6001依次逐个循环至8000进行操作运算,消耗的总时间除以2000,记为改进VSM模型算法的测试时间. 紧接着,本文使用BLAST本地构建6000条参考数据库,使用blastn程序对2000条待测样本进行逐一运算,输出结果,其花费的时间除以2000,同样记为blast算法测试时间. 说明1.这里使用blastn命令: blastn -query 6001.fa -db Sequence6000 -evalue 1e-5 -out blast6001.xls -outfmt 6 -num_alignments 10 -num_threads 1 说明2.以上参数中,-query6001.fa为待测样本G6001的fa格式文件,-db Sequence6000表示6000条参考样本的本地化数据库,-evalue 1e–5表示控制误差,-outfmt 6表示输出文件排版格式按照格式6进行输出,-num_alignments 10表示输出排名前10的序列结果,-num_threads 1表示单线程. 说明3.本文使用改进VSM算法,使用的是c程序,改进VSM算法和blastn算法均在Ubuntu 12.04.4 LTS同一个操作环境下运行. 最后,综合上述两项内容的操作,本文给出了改进VSM模型算法和BLAST算法运行时间. 表1 改进VSM算法与BLAST算法运行效率(单位:ms) 2.4.3 改进VSM算法运算效率与BLAST算法排名结果 本文选择输出前10名用于比较两种算法的鉴定效果,原因在于:本文使用的参考数据集序列数量为随机抽样后的6000条序列,序列数量相对较小;且在物种鉴定领域中,一般输出BLAST相似度98%以上的排名结果,这里使用BLAST输出序列相似度98%以上的序列数均小于10条,因此选择前10名作为评价的参考标准. 按照第2.2节的操作进行,本文得出了对应的排名结果,这里以待测样本G6001的排名结果为例,如表2所示. 表2 改进VSM算法与BLAST算法排名结果 本文K=8时,将改进VSM算法输出排名与blast排名结果重复率进行统计,最终得出:所有的2000个待测16S rRNA样本序列,通过使用改进VSM算法输出的前十名排名结果,其检出率已达到98.0%. 此外,若将输出前10名序列信息,改为输出前50,或前100名,我们发现检出率和K相关,随着K越大,算法的检出率相对会越优;且当K=10,输出前100名序列信息时,检出率达到了97.6%,证明了该算法的收敛性. 2.4.4 改进VSM算法与blast算法对比综合分析 根据表2,我们可以看到:随着K由4逐步递增至K=8,其输出的排名结果检出率由30%上升至90%;此外,G6000的排名也逐渐靠前,以及排名第一的G5997和BLAST的第1名结果吻合. 根据表1,我们可以看出,随着K的增大,运算时间也成约4倍递增,然而当K=8时,BLAST运算时间约为改进VSM模型算法的50倍. 综合以上运算效率和排名结果两方面的分析,我们可以得出改进VSM算法维持了其计算效率的优越性,并改进了排名结果,提高了检出率. 本文提出的改进VSM算法,是将经典文献中的K串组份向量空间模型算法应用于微生物16S rRNA序列的物种鉴定中,并对遗传距离公式进行改进,以期克服传统VSM模型算法在物种鉴定方面上的不足,进一步提高物种鉴定的检出率,最终保证物种鉴定的质量效果. 后续的研究工作还包括:改进VSM模型算法多线程模板设置,进一步提升该算法的运算效率.初步设置思路为:将参考数据集划分成多个模块,然后将待测样本分别与各个模块进行比对,输出各自的遗传距离向量,接着将各个向量汇集成一个完整的向量,最终对该向量进行排序输出最终结果.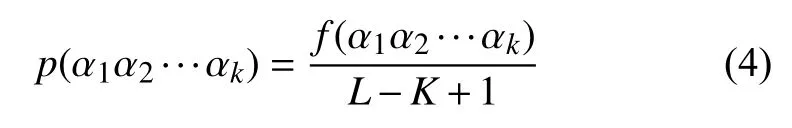
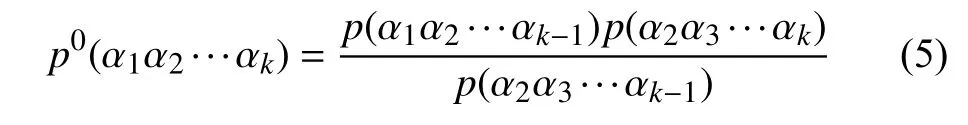
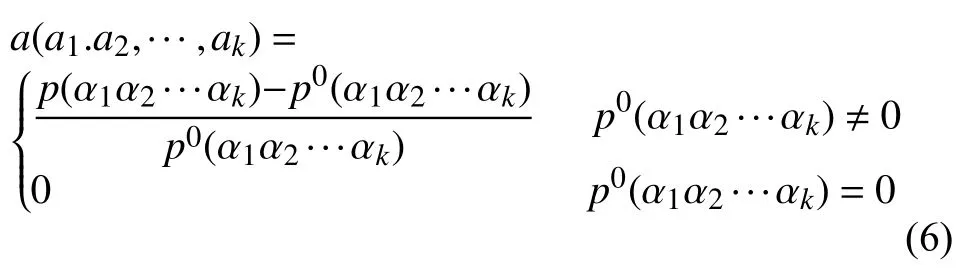
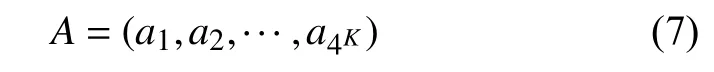
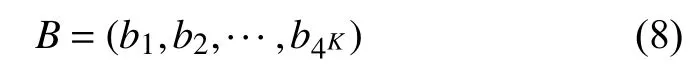
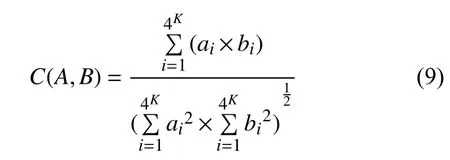
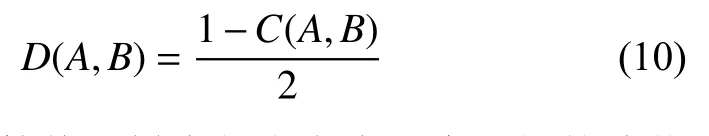
2.3 巴拿赫空间下等价替换的遗传距离公式
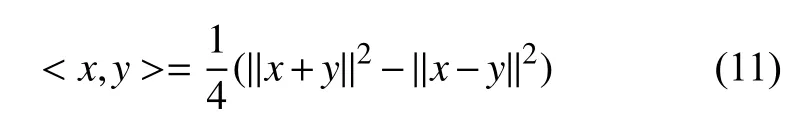
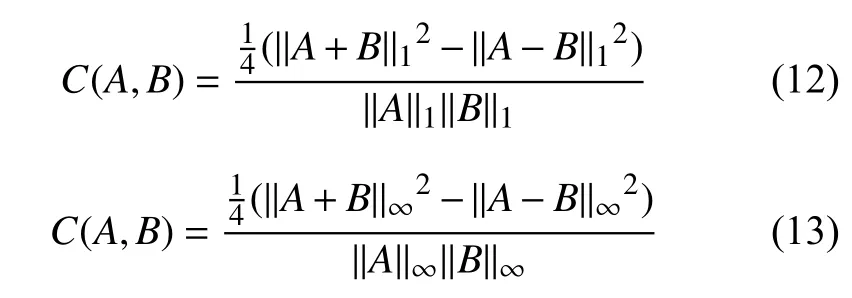
2.4 改进VSM模型算法[23,24]运算效率和排名结果分析

3 展望

