风力发电系统稳定性研究与分析
张 军
(兰州石化职业技术学院电子电气工程学院,甘肃 兰州 730060)
0 引言
风能是可再生能源中较为廉价、具有较大发展空间的清洁能源。其发展迅速,具有大规模开发和商业利用价值。作为新型能源,风能的稳定性不佳。在能量的转换过程中,风力发电系统对气流速度的影响不明显,并不会对当地的环境造成太大的影响或污染。风力发电系统对控制温室气体排放、污染等方面有突出的作用,同时可以较好地促进经济与人口的协调发展,受到了世界各国的广泛关注[1]。近年来,各国都在积极研究风力发电产能的开发与应用,使得风能得到了迅速的发展及应用。由于风力发电技术[1]应用广泛,受环境气候和时间、空间的影响,风力的大小和方向是时刻变化的,使得风能的不稳定因素增加。因此,风能在利用过程中存在很多问题。
针对风力发电的不稳定性,学者们采用了诸多研究策略。文献[2]采用离网运行的小型风力发电系统,并在传统“三相不控整流器-Buck电路-负载”的系统结构上研究先进的控制算法。该控制算法能起到一定的控制作用,但离网系统负载形式单一、可选择范围狭窄,使其应用范围有限。文献[3]提出了一种控制算法。该算法采用最大功率点跟踪(maximum power point tracking,MPPT)进行精度控制、速度追踪与动态响应,以达到控制的目的,试验证明了该算法的有效性。文献[4]同样在MPPT控制的基础上,提出一种高风速保护的控制方法,来拓宽系统的高风速性能,并证明了该算法的有效性。本文采用混合动力发电机系统,通过一个整流器和一个直流/直流(direct current/direct current,DC/DC)转换器与DC总线连接,多极永磁同步发电机(multi-ploe permanent magnet synchronous generator,MPMSG)允许无齿轮耦合至涡轮机,从而提高系统的鲁棒性。
1 风力发电系统建模
在风力发电系统中,根据结构,系统可以分为风能转换系统、传动系统、发电机系统等相互关联的子系统。该风力发电系统拓扑结构如图1所示。

图1 风力发电系统拓扑结构图
从图1中可以看出,系统由DC-DC整流器、逆变器和电池组成。各变换器的开关频率分别为100 kHz、100 kHz 和 20 kHz。各个部件互相配合,保障了风力发电系统的稳定运行。
1.1 风速建模
风场的风速是风力发电系统的关键考虑因素之一。风速可以用瞬时风速和平均风速来表征。瞬时风速定义为系统在短时间发生的实际风速。平均风速则是一段时间间隔之内风力发电机组瞬时风速的平均值。由于风的变化是不定的,因此通过不同地点的风向、风速对风电机组进行定量衡量,以促进风力发电机组更好地运行。
气动功率调节作为衡量风速的因素,用于参数分析。当风力发电机组的实际风速较大时,其功率受到风力发电机、变流器、控制系统等影响。因此,通过降低风轮的能量、减少叶片的承受载荷,提高实际风机的输出功率,使风力发电系统的输出功率保持在额定范畴之内。在风机的整个运行过程中,根据风机从切入风速到切出风速的不同,得到风力发电机的不同动态特性。风轮气动功率调节曲线如图2所示。从图2中可以看出,由于额定风速的不同,额定功率也在变化。具体的额定功率可分为部分负荷和满负荷这2个区域[5]。

图2 风轮气动功率调节曲线
在风速的额定范围内,通过空气制动法来限制控制子系统对系统的影响,进而对功率系数参数进行限制,以改变风轮的动力。通过风力发电机组的叶片外形特性来调节功率的大小,称为被动控制;通过改变叶片位置以适应风电机组的旋转水平的方法,称为主动控制。这些控制方案的目的是将整个风轮转向侧风,以减小空气动力效率[6]。
空气动力的重点在于对叶片的角度进行调节,使风机的风速随着桨距角的减小而增大。因此,空气动力受到叶片角度的影响。
简单的风速模型可以通过四分量确定[7],分别为平均风速、阵风风速、阶跃风速和随机风速。
Vw=VWB+VWG+VWS+VWN
(1)
式中:VWB为平均风速;VWG为阵风风速,是风速突变的特性;VWS为阶跃风速;VWN为随机风速。
(2)
式中:t1G为阵风的开始时间;t2G为阵风的结束时间;VGmax为阵风的最大风速。
(3)
式中:t1S为启动时间;t2S为终止时间;tS为保持时间;VSmax为阶跃峰值。
1.2 传动机构建模
本文所研究的风力发电机为直驱型,机组由低速轴、齿轮箱、高速轴、风轮及发电机构成。传动系统可以用三质量块模型准确描述,但需要全面的参数才能建模并仿真。本文采用风轮、发电机等进行建模[8]。其运动方程可表示为:
(4)
式中:Jr为转动惯量,kgm2;Ω为转动角速度,rad/s;Twtr为动力矩,Nm;TD为能力吸收的阻力矩,Nm;k为齿轮的传动比;Tm为扭矩。
发电机的运动方程可表示为:
(5)
式中:Jg为发电机转动惯量,kgm2;ωg为发电机的机械角速度,rad/s;Tm为高速轴上的扭矩,Nm;Te为发电机上的反扭矩,Nm。
通过与风力发电机的数学模型结合,当TD=0时,得到传动系统模型为:
(6)
1.3 发电机建模
对同步发电机的动态性能作进一步的分析。设d轴为永磁体转自极中心线,q轴则超前d轴90°。建立d、q轴数学模型,电压方程为[9]:
(7)
(8)
根据式(7)、式(8),电磁转矩方程可表示为:
Te=1.5p(φsdisq-φsqisd)
(9)
由式(9)可知,永磁同步发电机的电磁转矩与其定子电流的大小成正比。通过调节永磁同步发电机的电磁转矩,可以改变电流的大小,进而调节永磁同步发电机的转速,使永磁同步发电机能达到其额定输出功率[10]。
本文通过对以上风力发电系统建模,分析风机的运行情况。但实际的风力发电系统功率和额定容量不同。为了避免对模型阶数的过高要求,以及仿真时间过长等因素对仿真效率的严重影响,在建模时,应尽量降低系数的维数,从而提高系统的准确度、减少运行时间、提高仿真效率。
2 风力发电系统运行控制及稳定性分析
2.1 系统的运行控制
由于风的方向及大小不同,使得系统性能不稳定,极大地影响了系统正常运行。风速是时刻变化的。根据风力发电机组的运行方式不同,其输出功率如图3所示。图3中:Va为切入风速;Vb为额定风速;Vc为切除风速。根据各个区域的不同控制方法和特点,对风力发电机采用混合动力系统的调节方法[11-12]。

图3 风力发电机输出功率图
发电机混合动力系统(generator hybrid power system,GHPS)存在许多不同的拓扑结构。本文所考虑的发电机混合动力系统的原理如图4所示。其风力涡轮机的固定桨距直接连接到MPMSG上,通过一个整流器和一个DC/DC转换器与DC总线连接[12]。PMSG允许无齿轮耦合至涡轮机,提高了系统的鲁棒性和效率。光伏发电子系统也与直流母线连接。总线电压由电池组施加。可变备选载荷使用静态逆变器馈电。
风力发电子系统具有叶片涡轮俯仰变速拓扑功能。这意味着风力发电的电力对应的功率也输入到DC总线。因此,必须由电子控制涡轮机的转速调节。
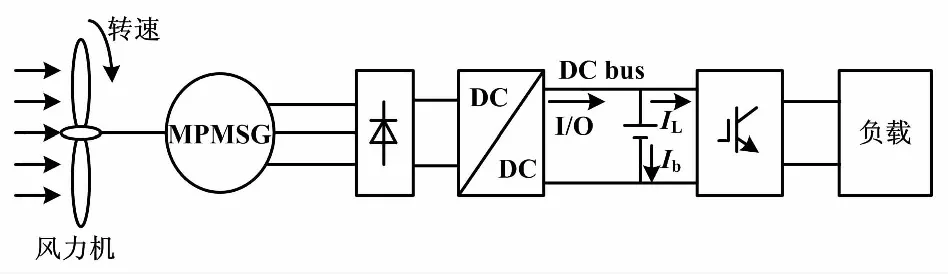
图4 混合发电动力系统原理图
风力发电的控制目标是充分利用充电的电池组,调节风力发电以满足负载需求,本文对光伏阵列进行控制。该发电阵列产生的功率通过太阳能子系统注入DC总线,电流的变化是由于太阳的随机性辐射造成的。
2.2 系统的稳定性分析
本文考虑到风电发电系统为单输入、双输出,所以有两个传递函数。
电压的输出传递函数可表示为:
(10)
由传递函数求出系统的零极点分布图、奈奎斯特图,分别如图5和图6所示。

图5 零极点分布图

图6 奈奎斯特图
从图5可以看出,零极点在左平面内,则系统开环零极点全部分布于左半平面;图6则没有包含点(-1,j0)。因此,说明了该系统是不稳定的。
3 仿真分析
为了验证本文所提方法的正确性,通过Matlab搭建仿真模型并进行仿真分析。仿真结果如图7所示。本文参数设置如下,风力发电的额定风速设置为12 m/s,叶轮半径为25 m,桨距角为0,永磁同步风力发电机的额定功率为1.5 MW,极对数为48,定子阻值为0.28 Ω,风力发电机的输出电压为690 V,风机的额定频率为50 Hz,直流侧电压值为1 100 V,直流侧电容为2 200 μF,仿真时间为10 s。
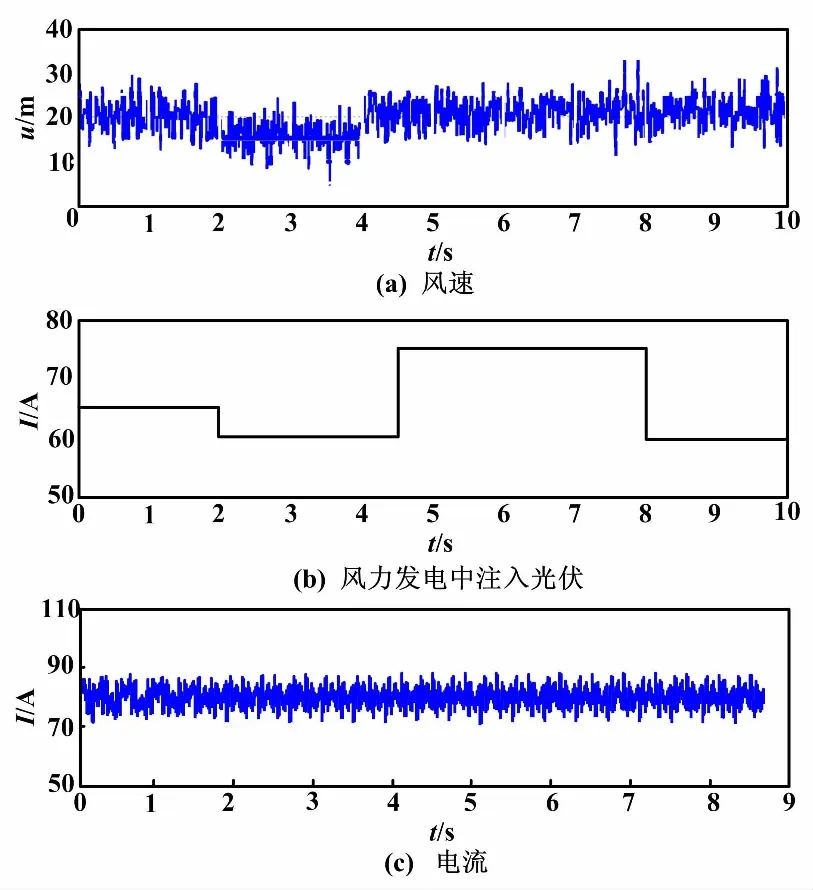
图7 仿真结果图
对以上三个仿真图进行对比,可以看出,当风速在2 s时的注入电流为65 A,4.5 s时升至75 A,8 s时降为60 A。在整个过程中,永磁同步风力发电机的电流基本控制趋于平稳,不再波动。
4 结束语
本文对风力发电系统的稳定性能进行了研究。首先,分析了影响风力发电系统的因素,并构建了风力发电系统模型,对各个重要的部件进行说明;然后,采用混合动力发电机系统,通过一个整流器和一个DC/DC转换器与DC总线连接,提高系统的鲁棒性,并通过注入电流验证控制方案的合理性;最后,采用仿真模型进行验证,通过判断零极点分布图和奈奎斯特图对系统进行稳定性分析,证明了该控制方法能够使系统稳定运行。

