动态偏最小二乘在软测量建模方法中的应用

高世伟，王忠民，洪梓榕

(1.兰州石化职业技术学院电子电气工程学院，甘肃 兰州 730060；2.中国石油兰州石化公司自动化研究院，甘肃 兰州 730060)

0 引言

软测量技术依据可测特别是易测的变量，通过构建数学模型，对难以直接测量的变量进行预估。由于工业生产过程一般来说比较复杂，并且具有明显、固有的非线性特征，所以采用严格的理论建模方法往往不切实际[1]。因此，基于数据驱动的软测量技术得到了广泛的研究和发展。其中，多元线性回归(multiple linear regression，MLR)是基本的软测量模型[2-3]。主成分分析法(principal component analysis，PCA)和偏最小二乘法(partial least square method，PLS)是应用广泛的多元回归技术，也被用于软测量建模[4-6]。为适应过程的动态特性，还开发了动态主成分分析法(dynamic principal component analysis，DPCA)和动态偏最小二乘法(dynamic partial least squares，DPLS)等方法[7-9]。基于DPLS的软测量在不同类型的工业生产过程中得到了广泛应用[10-11]。但在执行DPLS时，如输入数据矩阵中增加较多的滞后测量值会增加矩阵的维数，实施多元回归需要较大的计算量。

本文采用一种改进的DPLS方法。该方法不仅减小了模型尺寸，而且能改善预测效果。

1 偏最小二乘回归

PLS算法是由Wold等人发明的多元统计数据分析方法[12]。它利用某些辅助变量来预测主要变量，当各变量内部高度线性相关时，这种方法非常有效。设X∈Rm×n、Y∈Rn×q分别表示输入数据矩阵和输出数据矩阵，n是样本数，m是样本中的变量数，q是因变量数量。假设X和Y线性相关：

Y=XC+V

(1)

式中：C为系数矩阵；V为噪声矩阵。

PLS首先将数据矩阵X和Y分解成双线性项，得到线性模型：

X=TPT+E

(2)

Y=UQT+F

(3)

式中：T∈Rn×a和U∈Rn×a分别为X和Y的得分矩阵；a为保留的PLS成分数量；P∈Rm×a和Q∈Rp×a为载荷矩阵；E和F为残差矩阵，是运用偏最小二乘法拟合矩阵X和Y时引入的误差。PLS的目的是尽可能多地描述Y的变化，可以通过内部线性模型将X和Y相关联：

U=TB+R

(4)

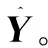
(5)

2 降维DPLS软测量方法

基于DPLS的软测量可以为开环和闭环数据提供主要变量的无偏估计[13-14]，是一个动态的估计器，可充分捕获过程动态特性。它的基本思想是利用增量测量(滞后数据)来捕获过程动态特性。通常使用子空间辨识框架推导出DPLS软测量公式。在子空间辨识中，一个随机线性系统可以用以下形式表示：

(6)

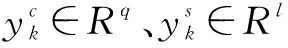
为了获得动态软测量公式，将系统方程转化为预测形式[13]：

(7)

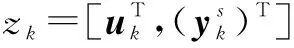
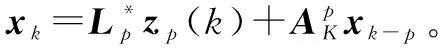
(8)

同样，依据式(7)中的状态空间描述，可以得到扩展的输出方程：

(9)

(10)

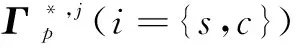
(11)

(12)

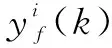
(13)

(14)

当p较大时，式(9)、式(10)可以简化为：

(15)

为便于系统矩阵的估计，通常需要n

(16)

(17)

式中：dui为第i个输入和所求关键参数之间的延时；dyj为第j个辅助输出与关键参数之间的延时。

通过引入过程延迟信息，有效减小了回归器的维数。改进后的DPLS软测量方法存在辅助变量选择的问题。选择不适当的辅助变量作为软测量的输入，会降低预测精度。只有选用那些对主变量最敏感的辅助变量，才有可能获得满意的效果。

下一个关键步骤是估计与不同变量相关的延迟。对于工业生产过程中不同位置收集的测量值，相关的传输延迟是不同的。通过识别每个相关联的延迟时间，可以有效地减少系统阶数。为了提取主要输出和辅助输出之间的动态关系，必须确定所需的过去时间范围。对于线性系统，可根据动态系统的阶数来确定过去时间范围。对于非线性系统，选取的过去时间范围可以更大，以获得与实际非线性关系更好的线性近似[17]。

3 仿真试验

接下来验证引入降维方法后的DPLS性能。DPLS与降维DPLS的预测对比如图1所示。

图1 DPLS与降维DPLS预测对比图

在丁苯橡胶生产过程中，转化率是表征聚合反应进程的一项重要质量指标参数，数值越高，说明转化率越高。生产厂家多采用人工间歇化验的方法取得，但是通常人工化验周期长，装置操作人员无法及时获得转化率数据，就无法对装置产生的波动及时跟踪并进行处理。因此，实现转化率数据的在线测量，对于提高装置生产效率具有非常重要的作用。目前,国内外没有能够在线测量橡胶转化率的仪表，但是软测量技术在橡胶转化率的测量已有一些研究[17]。基于前期的研究成果[18-19]，在研究中选取垂直差压、水平差压、反应釜周围环境温度、反应釜搅拌功率、装置管道压力、胶浆温度、乙烯混合总流量等信号为关键参数。收集160组生产历史数据，在经过滤波等预处理后进行模型仿真。对于DPLS和降维后的DPLS，选择相同的历史数据建立软测量，并将两种模型预测数据分别与人工化验测量数据进行对比。

两种在线检测方法预测数据的变化趋势与试验室分析得到的转化率变化趋势基本吻合，都能较好地满足工艺控制的实际需要。为了从数据上评估两种软测量技术的性能，采用两种预测值与化验分析值的均方根误差进行对比。均方根误差能够很好地反映测量的精密度。通过计算可知，DPLS与降维后DPLS的均方根误差分别为1.964 1和1.705 6。由此可以看出，新的方法提高了模型预测能力。新方法有效地减小了回归器的维数，特别是当处理的数据较多，且变量数较大时计算量也会较DPLS低。

4 结束语

本文采用一种降维的DPLS方法进行软测量模型建立。通过估计过程中涉及的传输延迟，将时移变量作为回归变量来减少系统的阶数，从而减少了预测所需的过去时间。这样不仅可以获得提供优良性能的降维后模型，而且可以实现多步预测。通过对丁苯橡胶生产过程的仿真，证明了该方法的有效性。该方法为今后软测量模型的研究提供了一种思路。